
 |
|
|
|
|
|
|
|
|
|
|
Click here for a list of measurements (including updates) which have been released since the cut-off for inclusion in this set of averages
Measurements related to the CKM angle β ≡ φ1:
Measurements related to the CKM angle α ≡ φ2:
Legend: if not stated otherwise,
We use Combos v3.20 (homepage, manual) for the rescaling of the experimental results to common sets of input parameters.
The experimental results have been rescaled to a common set of input parameters (see table below).
| Parameter | Value | Ref. / Comments |
|---|---|---|
| τ(Bd) | (1.527 ± 0.008) ps | HFAG - Oscillations/Lifetime |
| Δmd | (0.508 ± 0.004) ps−1 | HFAG - Oscillations/Lifetime |
|
|A⊥|2 (CP-odd fraction in B0→ J/ψK* CP sample) |
0.245 ± 0.015 ± 0.004 (note: acceptance-corrected central value; the uncorrected value is: 0.230) |
BABAR: PRD 71 (2005) 032005 |
| 0.195 ± 0.012 ± 0.008 | Belle: PRL 95 (2005) 091601 | |
| 0.217 ± 0.010 | Average |
Additional note on commonly treated (correlated) systematic effects:
We obtain for sin(2β) ≡ sin(2φ1) in the different decay modes:
| Parameter: sin(2β) ≡ sin(2φ1) | ||||
|---|---|---|---|---|
| Mode | BABAR | Belle | Average | Ref. / Comments |
| Charmonium: | N(BB)=227m | N(BB)=386m | - |
BABAR: PRL 94 (2005) 161803
BELLE-CONF-0569 (hep-ex/0507037) |
| J/ψKS, ψ(2S)KS, χc1KS, ηCKS (ηCP=-1) | 0.75 ± 0.04stat | 0.668 ± 0.047stat (J/ψKS only) | ||
| J/ψKL (ηCP=+1) | 0.57 ± 0.09stat | 0.619 ± 0.069stat | ||
| J/ψK*0 (K*0 → KSπ0) | 0.96 ± 0.32stat | - | ||
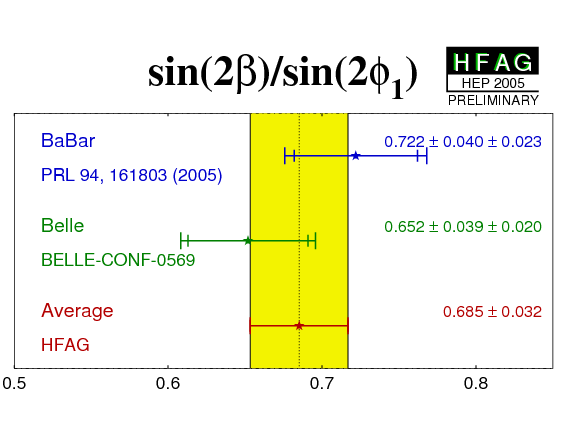
| All charmonium | 0.722 ± 0.040 ± 0.023 | 0.652 ± 0.039 ± 0.020 |
0.685 ± 0.032
(0.028stat-only) |
CL = 0.27 |
Including earlier sin(2β) ≡ sin(2φ1) measurements using Bd → J/ψKS decays:
| Parameter: sin(2β) ≡ sin(2φ1) | ||||
|---|---|---|---|---|
| Experiment | Value | Ref. / Comments | ||
| ALEPH | 0.84 +0.82−1.04 ± 0.16 | PL B492 (2000) 259-274 | ||
| OPAL | 3.2 +1.8−2.0 ± 0.5 | EPJ C5 (1998) 379-388 | ||
| CDF (full Run I) | 0.79 +0.41−0.44(stat+syst) | PRD 61 (2000) 072005 | ||
we find the only slightly modified average:
| Parameter: sin(2β) ≡ sin(2φ1) | ||||
|---|---|---|---|---|
| All charmonium | 0.687 ± 0.032 (0.028stat-only) | CL = 0.48 | ||
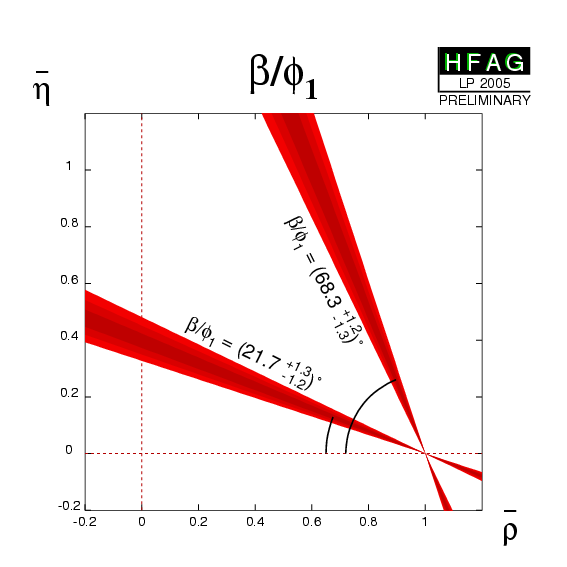
from which we obtain the following solutions for β ≡ φ1 (in [0, π])
| β ≡ φ1 = (21.7 +1.3−1.2)° | or | β ≡ φ1 = (68.3 +1.2−1.3)° |
Plots:
| Average of sin(2β) ≡ sin(2φ1) from all experiments. |

eps.gz png |
|||
| Averages of sin(2β) ≡ sin(2φ1) and C=-A from the B factories. |
eps.gz png |
eps.gz png |
||
| Constraint on the ρ-bar-η-bar plane: |
eps.gz png |

eps.gz png |
||
|
Constraining the Unitarity Triangle (ρ, η):
Visit the CKMfitter and UTfit sites for results on global CKM fits using different fit techniques and input quantities. |
Historically the experiments determined |λ| for the charmonium modes; more recently the parameters C = −A = (1−|λ|2)/(1+|λ|2) are being used, as they are in all other time-dependent CP analyses. We recompute C from |λ| for the following averages.
| Parameter: C=−A (if not stated otherwise) | ||||
|---|---|---|---|---|
| Mode | BABAR | Belle | Average | Ref. / Comments |
| Charmonium | N(BB)=227m | N(BB)=386m | - |
BABAR: PRL 94 (2005) 161803
BELLE-CONF-0569 (hep-ex/0507037) |
| J/ψKS, ψ(2S)KS, χc1KS, ηCKS |
|λ| = 0.950 ± 0.031 ± 0.013
C = 0.051 ± 0.033 ± 0.014 |
C = 0.021 ± 0.034stat (J/ψKS only) | ||
| J/ψKL | C = −0.049 ± 0.039stat | |||
| J/ψK*0 (K*0 → KSπ0) | - | |||
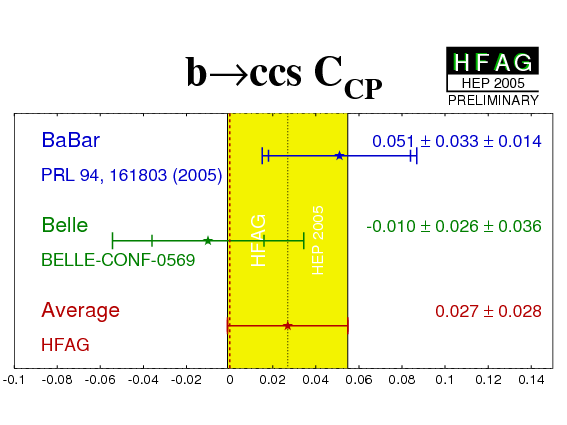
| All charmonium | −0.010 ± 0.026 ± 0.036 |
0.026 ± 0.041
(0.020stat-only) |
CL = 0.31 | |
Digression and plots:
|
Constraining CJ/ψ Ks from
ACP(B+ → J/ψ K+)
and ASL:
As suggested by Y. Nir, one can obtain a powerful SM constraint on |λ| = |q/p||A-bar/A| via the relations ASL = (1−|q/p|4)/(1+|q/p|4) and ACP(B+ → J/ψ K+) = (|A-bar/A|2−1)/(|A-bar/A|2+1), where ASL denotes the CP asymmetry in semileptonic B decays, and ACP(B+ → J/ψ K+) is the CP-violating charge asymmetry measured in B+ → J/ψ K+ decays. We take the ASL result from the HFAG oscillation group, ASL = −0.0026 ± 0.0067, and average the ACP(B+ → J/ψ K+) results from BABAR, Belle and CLEO, to find ACP(B+ → J/ψ K+) = −0.007 ± 0.019. These give |q/p| = 1.0013 ± 0.0034 and |A-bar/A| = 0.993 ± 0.018, and hence |λ|indirect = 0.994 ± 0.018, corresponding to C = 0.006 ± 0.018. Discussion: the amplitude relation between neutral and charged B → J/ψ K decays has been found by Fleischer-Mannel to hold up to negligible corrections of the order O(λ3). However, the identification of |λ|, measured through the C coefficient in B0 → J/ψ K0, with |q/p||A-bar/A| assumes ΔΓBd=0. The systematic error on C from a width difference ΔΓBd/ΓBd~0.02 has been estimated by BABAR to be 0.0009. |
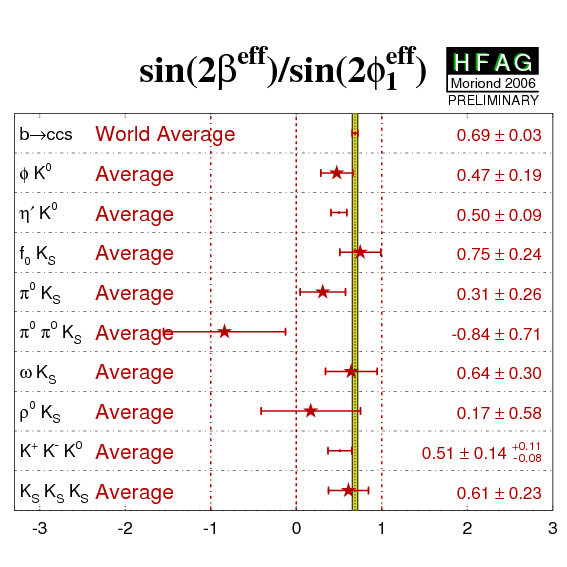
| Parameter: sin(2βeff) ≡ sin(2φ1eff) | ||||
|---|---|---|---|---|
| Mode | BABAR N(BB)=209-227m |
Belle N(BB)=386m |
Average | Ref. / Comments |
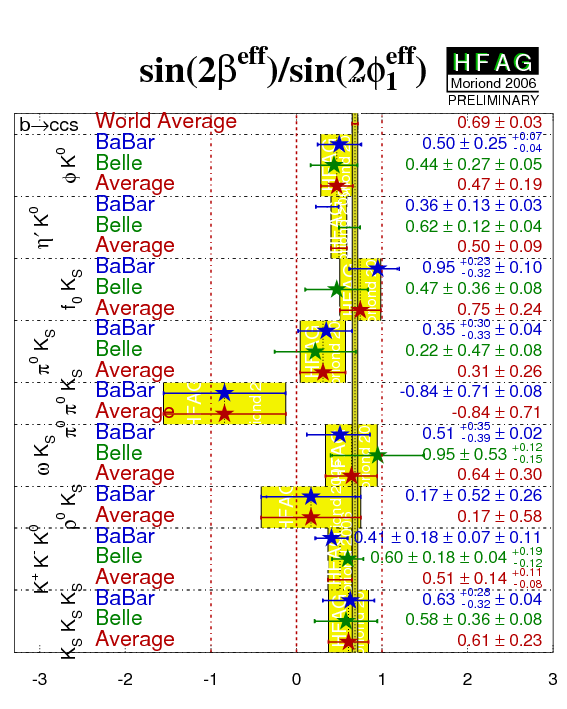
| φK0 | 0.50 ± 0.25 +0.07−0.04 | 0.44 ± 0.27 ± 0.05 | 0.47 ± 0.19 CL=0.87 (0.2σ) |
BABAR: PRD 71 (2005) 091102(R)
BELLE-CONF-0569 (hep-ex/0507037) |
| η′K0 | 0.36 ± 0.13 ± 0.03 | 0.62 ± 0.12 ± 0.04 | 0.50 ± 0.09 CL=0.16 (1.4σ) |
BABAR-CONF-05/014 (hep-ex/0507087)
BELLE-CONF-0569 (hep-ex/0507037) |
| f0KS | 0.95 +0.23−0.32 ± 0.10 | 0.47 ± 0.36 ± 0.08 | 0.75 ± 0.24 CL=0.32 (1.0σ) |
BABAR-CONF-04/019 (hep-ex/0408095)
BELLE-CONF-0569 (hep-ex/0507037) |
| π0KS | 0.35 +0.30−0.33 ± 0.04 | 0.22 ± 0.47 ± 0.08 | 0.31 ± 0.26 CL=0.82 (0.2σ) |
BABAR: PRD71 (2005) 111102
BELLE-CONF-0569 (hep-ex/0507037) |
| π0π0KS | −0.84 ± 0.71 ± 0.08 | - | −0.84 ± 0.71 | BABAR-CONF-05/020 (hep-ex/0508017) |
| ωKS | 0.51 +0.35−0.39 ± 0.02 | 0.95 ± 0.53 +0.12−0.15 | 0.64 ± 0.30 CL=0.49 (0.7σ) |
BABAR-PUB-06/016 (hep-ex/0603040)
(submitted to PRL)
BELLE-CONF-0569 (hep-ex/0507037) |
| ρ0KS | 0.17 ± 0.52 ± 0.26 | - | 0.17 ± 0.58 | IN PREPARATION |
|
K+K−K0
(excluding φK0) |
0.41 ± 0.18 ± 0.07 ± 0.11CP-even
(fCP-even= 0.89 ± 0.08 ± 0.06 [moments]) |
0.60 ± 0.18 ± 0.04 +0.19−0.12CP-even
(fCP-even= 0.93 ± 0.09 ± 0.05 [SU(2)]) |
0.51 ± 0.14 +0.11−0.08 CL=0.38 (0.9σ) (rescaled to average fCP-even= 0.91 ± 0.07) |
BABAR-CONF-05/002 (hep-ex/0507016)
BELLE-CONF-0569 (hep-ex/0507037) |
| KSKSKS | 0.63 +0.28−0.32 ± 0.04 | 0.58 ± 0.36 ± 0.08 | 0.61 ± 0.23 CL=0.92 (0.1σ) |
BABAR-CONF-05/012 (hep-ex/0507052)
BELLE-CONF-0569 (hep-ex/0507037) |
| Naïve b→s penguin average | 0.50 ± 0.06 | CL=0.82 (0.2σ) | ||
| Direct comparison of charmonium and s-penguin averages (see comments below): CL=0.0092 (2.6σ) | ||||
Please note that
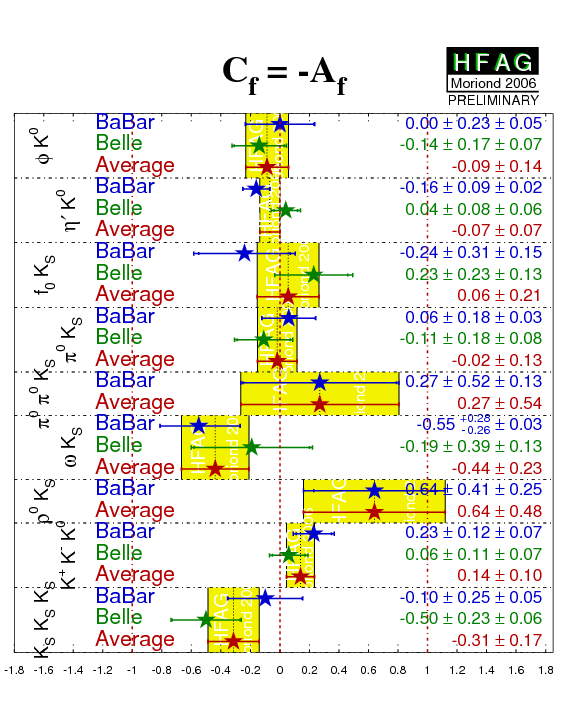
The cosine coefficient:
| Parameter: C=−A (if not stated otherwise) | ||||
|---|---|---|---|---|
| Mode | BABAR N(BB)=209-227m |
Belle N(BB)=386m |
Average | Ref. / Comments |
| φK0 | 0.00 ± 0.23 ± 0.05 | −0.14 ± 0.17 ± 0.07 | −0.09 ± 0.14 CL=0.64 (0.5σ) |
BABAR: PRD 71 (2005) 091102(R)
BELLE-CONF-0569 (hep-ex/0507037) |
| η′K0 | −0.16 ± 0.09 ± 0.02 | 0.04 ± 0.08 ± 0.06 | −0.07 ± 0.07 CL=0.14 (1.5σ) |
BABAR-CONF-05/014 (hep-ex/0507087)
BELLE-CONF-0569 (hep-ex/0507037) |
| f0KS | −0.24 ± 0.31 ± 0.15 | 0.23 ± 0.23 ± 0.13 | 0.06 ± 0.21 CL=0.28 (1.1σ) |
BABAR-CONF-04/019 (hep-ex/0408095)
BELLE-CONF-0569 (hep-ex/0507037) |
| π0KS | 0.06 ± 0.18 ± 0.03 | −0.11 ± 0.18 ± 0.08 | −0.02 ± 0.13 CL=0.53 (0.6σ) |
BABAR: PRD71 (2005) 111102
BELLE-CONF-0569 (hep-ex/0507037) |
| π0π0KS | 0.27 ± 0.52 ± 0.13 | - | 0.27 ± 0.54 | BABAR-CONF-05/020 (hep-ex/0508017) |
| ωKS | −0.55 +0.28−0.26 ± 0.03 | −0.19 ± 0.39 ± 0.13 | −0.44 ± 0.23 CL=0.46 (0.7σ) |
BABAR-PUB-06/016 (hep-ex/0603040)
(submitted to PRL)
BELLE-CONF-0569 (hep-ex/0507037) |
| ρ0KS | 0.64 ± 0.41 ± 0.25 | - | 0.64 ± 0.48 | IN PREPARATION |
|
K+K−K0
(excluding φK0) |
0.23 ± 0.13 | 0.06 ± 0.11 ± 0.07 | 0.15 ± 0.09 CL=0.36 (0.9σ) |
BABAR-CONF-05/002 (hep-ex/0507016)
BELLE-CONF-0569 (hep-ex/0507037) |
| KSKSKS | −0.10 ± 0.25 ± 0.05 | −0.50 ± 0.23 ± 0.06 | −0.31 ± 0.17 CL=0.25 (1.1σ) |
BABAR-CONF-05/012 (hep-ex/0507052)
BELLE-CONF-0569 (hep-ex/0507037) |
| Naïve b→s penguin average | −0.04 ± 0.04 | CL=0.25 (1.2σ) | ||
| Compilation of results for −η×S ≈ sin(2βeff) ≡ sin(2φ1eff) and C from s-penguin decays. |
eps png |
eps png |
| Same, but without π0π0KS and ρ0KS, to allow closer inspection of the detail. |
|
|
| Naïve s-penguin averages |
|
|
| Comparisons of averages in the different b→q q-bar s modes |
eps png |

eps png |
| Same, but without π0π0KS and ρ0KS, to allow closer inspection of the detail. |
|
|
|
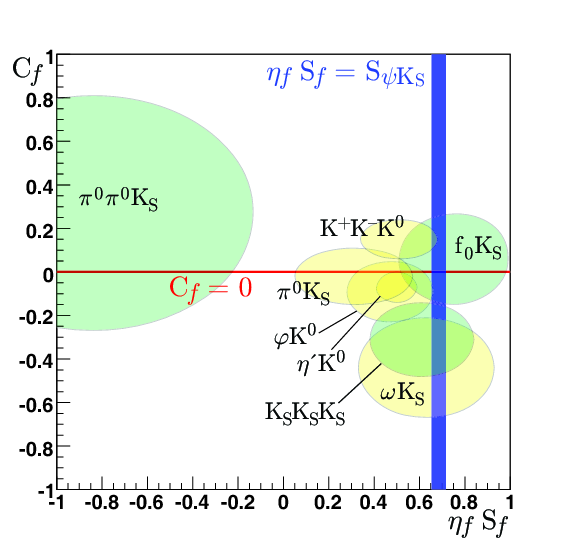
2D comparisons of averages in the different b→q q-bar s modes.
Taken from the PDG 2005 review on "CP Violation in Meson Decays" by D.Kirkby and Y.Nir. * This plot (and the averages) assume no correlations between the S and C measurements in each mode. |
eps png |
|
The BABAR and Belle collaborations have performed measurements of sin(2β) & cos(2β) ≡ sin(2φ1) & cos(2φ1) in time-dependent transversity analyses of the pseudoscalar to vector-vector decay B0→ J/ψK*, where cos(2β) ≡ cos(2φ1) enters as a factor in the interference between CP-even and CP-odd amplitudes. In principle, this analysis comes along with an ambiguity on the sign of cos(2β) ≡ cos(2φ1) due to an incomplete determination of the strong phases occurring in the three transversity amplitudes. BABAR resolves this ambiguity by inserting the known variation of the rapidly moving P-wave phase relative to the slowly moving S-wave phase with the invariant mass of the Kπ system in the vicinity of the K*(892) resonance. The result is in agreement with the prediction obtained from s-quark helicity conservation. It corresponds to Solution II defined by Suzuki, which is the phase convention used for the averages given here.
| Experiment | sin(2β) ≡ sin(2φ1)J/ψK* | cos(2β) ≡ cos(2φ1)J/ψK* | Correlation | Ref. / Comments |
|---|---|---|---|---|
|
BABAR'04
N(BB)=88m |
−0.10 ± 0.57 ± 0.14 | 3.32 +0.76−0.96 ± 0.27 | −0.37 | PRD 71 (2005) 032005 |
|
Belle'04
N(BB)=275m |
0.24 ± 0.31 ± 0.05 | 0.56 ± 0.79 ± 0.11
[using Solution II] |
+0.22 | PRL 95 (2005) 091601 |
| Average | IN PREPARATION (CL = → xσ) |
IN PREPARATION (CL = → xσ) |
? | See remark below table |
Note that due to the strong non-Gaussian character of the BABAR measurement (although the result is far positive, the confidence level for cos(2β)>0 is only 89%), the interpretation of the average given above has to be done with the greatest care.
Due to possible significant penguin pollution, both the cosine and the sine coefficients of the Cabibbo-suppressed b → cc-bar d decays are free parameters of the theory. Absence of penguin pollution would result in Scc-bar d = − ηCP sin(2β) ≡ − ηCP sin(2φ1) and Ccc-bar d = 0 for the CP eigenstate final states (ηCP = +1 for both J/ψπ0 and D+D−). For the non-CP eigenstates D*+−D−+, absence of penguin pollution (ie. no direct CP violation) gives A = 0, C+ = −C− (but is not necessarily zero), S+ = 2 R sin(2β+δ)/(1+R2) and S− = 2 R sin(2β−δ)/(1+R2). [With alternative notation, S+ = 2 R sin(2φ1+δ)/(1+R2) and S− = 2 R sin(2φ1−δ)/(1+R2)]. Here R is the ratio of the magnitudes of the amplitudes for B0 → D*+D− and B0 → D*−D+, while δ is the strong phase between them. If there is no CP violation of any kind, then S+ = −S− (but is not necessarily zero). The vector-vector final state D*+D*− is a mixture of CP-even and CP-odd; the longitudinally polarized component is CP-even. Note that in the general case of non-negligible penguin contributions, the penguin-tree ratio and strong phase differences do not have to be the same for each helicity amplitude (likewise, they do not have to be the same for D*+D− and D*−D+).
At present we do not apply a rescaling of the results to a common, updated set of input parameters.
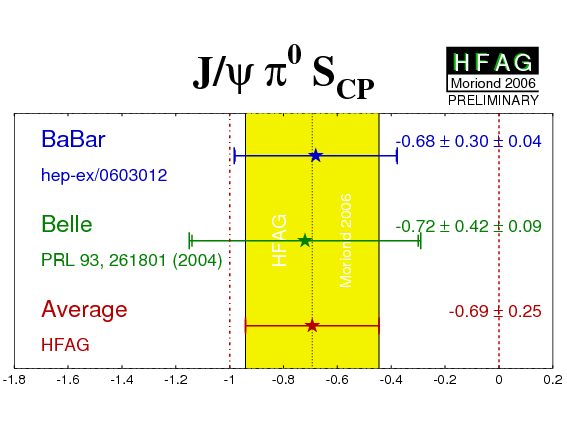
| Experiment | SJ/ψπ0 | CJ/ψπ0 = −AJ/ψπ0 | Correlation | Ref. / Comments | |
|---|---|---|---|---|---|
|
BABAR'06
N(BB)=232m |
−0.68 ± 0.30 ± 0.04 | −0.21 ± 0.26 ± 0.06 | 0.08 | PRD 74 (2006) 011101 | |
|
Belle'04
N(BB)=152m |
−0.72 ± 0.42 ± 0.09 | 0.01 ± 0.29 ± 0.03 | −0.12 | PRL 93 (2004) 261801 | |
| Average | −0.69 ± 0.25 CL=0.94 (0.1σ) |
−0.11 ± 0.20 CL=0.58 (0.6σ) |
uncorrelated averages | ||
|
|
eps png |

eps png |
|||
| Experiment | SD+D− | CD+D− | Correlation | Ref. / Comments |
|---|---|---|---|---|
|
BABAR'05
N(BB)=232m |
−0.29 ± 0.63 ± 0.06 | 0.11 ± 0.35 ± 0.06 | - | PRL 95 (2005) 131802 |
| Belle | NOT YET AVAILABLE | NOT YET AVAILABLE | - | - |
| Average | −0.29 ± 0.63 | 0.11 ± 0.36 | - | - |
We convert Im(λ) = S/(1 + C) and |λ|2 = (1 − C)/(1 + C), taking into account correlations:
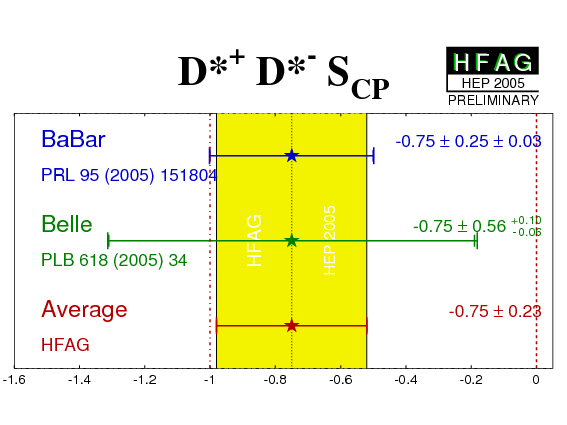
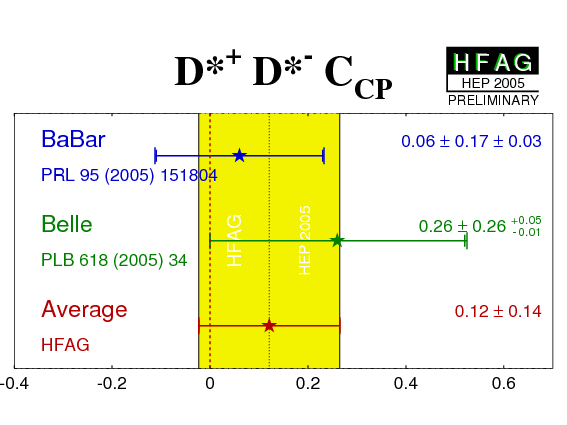
| Experiment | SD*+D*− | CD*+D*− | Correlation | Ref. / Comments | |
|---|---|---|---|---|---|
|
BABAR'05
N(BB)=227m |
−0.75 ± 0.25 ± 0.03 | 0.06 ± 0.17 ± 0.03 | Table |
PRL 95 (2005) 151804
RT = 0.125 ± 0.044 ± 0.007 |
|
|
Belle'04
N(BB)=152m |
−0.75 ± 0.56 ± 0.10 ± 0.06[RT] | 0.26 ± 0.26 ± 0.05 ± 0.01[RT] | - |
PLB 618 (2005) 34
RT = 0.19 ± 0.08 ± 0.01 |
|
| Average(*) | −0.75 ± 0.23 CL=1.00 (0.0σ) |
0.12 ± 0.14 CL=0.52 (0.6σ) |
uncorrelated averages | ||
|
|
eps png |
eps png |
|||
(*) Note that we have not pre-averaged the CP-odd fractions (and then accordingly rescaled the average sine coefficient). Since both data samples are independent, the results are (approximately) invariant under such a treatment, compared to the direct average that is performed here. Also: due to the lack of correlations coefficients, we have performed an uncorrelated average here.
| Experiment | S+−(D*+D−) | C+−(D*+D−) | S−+(D*−D+) | C−+(D*−D+) | A(D*+−D−+) | Correlations | Ref. / Comments |
|---|---|---|---|---|---|---|---|
|
BABAR'05
N(BB)=232m |
−0.54 ± 0.35 ± 0.07 | 0.09 ± 0.25 ± 0.06 | −0.29 ± 0.33 ± 0.07 | 0.17 ± 0.24 ± 0.04 | - | PRL 95 (2005) 131802 | |
|
Belle'04 N(BB)=152m (combined fully and partially rec. B decays) |
−0.55 ± 0.39 ± 0.12 | −0.37 ± 0.22 ± 0.06 | −0.96 ± 0.43 ± 0.12 | 0.23 ± 0.25 ± 0.06 | 0.07 ± 0.08 ± 0.04 | - | PRL 93 (2004) 201802 |
| Average | −0.54 ± 0.27 CL=0.99 (0.0σ) |
−0.16 ± 0.17 CL=0.18 (1.3σ) |
−0.53 ± 0.27 CL=0.23 (1.2σ) |
0.20 ± 0.18 CL=0.87 (0.2σ) |
0.07 ± 0.09 | uncorrelated averages |
| Compilation of results for (left) sin(2βeff) ≡ sin(2φ1eff) = −ηCPS and (right) C from time-dependent b → cc-bar d analyses with CP eigenstate final states. The results are compared to the values from the corresponding charmonium averages. |
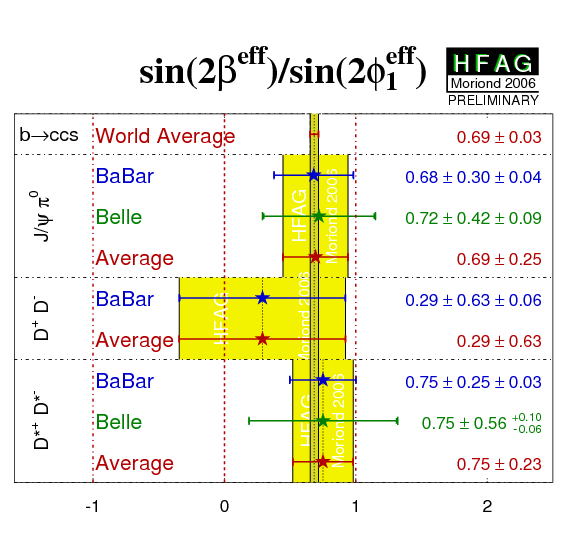
eps png |
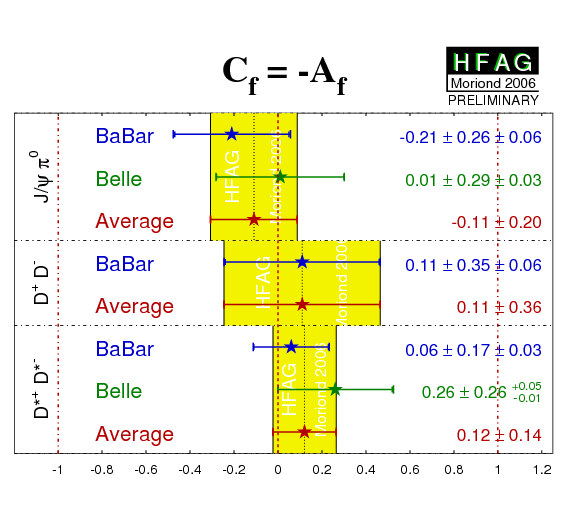
eps png |
Bd decays to final states such as Dπ0 are governed by the b → cu-bar d transitions. If one chooses a final state which is a CP eigenstate, ie. DCPπ0, the usual time-dependence formulae are recovered, with the sine coefficient sensitive to sin(2β) ≡ sin(2φ1). Since there is no penguin contribution to these decays, there is even less associated theoretical uncertainty than for b → cc-bar s decays like Bd → J/ψ KS.
Bondar, Gershon and Krokovny have shown that when multibody D decays, such as D → KSπ+π− are used, a time-dependent analysis of the Dalitz plot of the D decay allows a direct determination of the weak phase: β ≡ φ1. Equivalently, both sin(2β) ≡ sin(2φ1) and cos(2β) ≡ cos(2φ1) can be measured. This information allows to resolve the ambiguity in the measurement of 2β ≡ 2φ1 from sin(2β) ≡ sin(2φ1) alone.
Results of such an analysis are available from Belle. The decays Bd → Dπ0, Bd → Dη, Bd → Dω, Bd → D*π0 and Bd → D*η are used. The daughter decays are D* → Dπ0 and D → KSπ+π−.
At present we do not apply a rescaling of the results to a common, updated set of input parameters.
| Experiment | sin(2β) ≡ sin(2φ1) | cos(2β) ≡ cos(2φ1) | Reference / comments |
|---|---|---|---|
|
Belle'05
N(BB)=386m |
0.78 ± 0.44 ± 0.22 | 1.87 +0.40−0.53 +0.22−0.32 | hep-ex/0605023 (submitted to PRL) |
Note that direct measurements of phases often suffer from unusual and non-Gaussian behaviour. Belle determine the sign of cos(2φ)1 to be positive at 98.3% confidence level.
Time-dependent analyses of radiative b decays such as B0→ KSπ0γ, probe the polarization of the photon. In the SM, the photon helicity is dominantly left-handed for b → sγ, and right-handed for the conjugate process. As a consequence, B0 → KSπ0γ behaves like an effective flavor eigenstate, and mixing-induced CP violation is expected to be small - a simple estimation gives: S ~ −2(ms/mb)sin(2β) ≡ −2(ms/mb)sin(2φ1) (with an assumption that the Standard Model dipole operator is dominant). Corrections to the above may allow values of S as large as 10% in the SM.
Atwood et al. have shown that (with the same assumption) an inclusive analysis with respect to KSπ0 can be performed, since the properties of the decay amplitudes are independent of the angular momentum of the KSπ0 system. However, if non-dipole operators contribute significantly to the amplitudes, then the Standard Model mixing-induced CP violation could be larger than the expectation given above, and the CPV parameters may vary slightly over the KSπ0γ Dalitz plot, for example as a function of the KSπ0 invariant mass.
An inclusive KSπ0γ analysis has been performed by Belle using the invariant mass range up to 1.8 GeV/c2. Belle also gives results for the K*(892) region: 0.8 GeV/c2 to 1.0 GeV/c2. BABAR has measured the CP-violating asymmetries separately within and outside the K*(892) mass range: 0.8 GeV/c2 to 1.0 GeV/c2 is again used for K*(892)γ candidates, while events with invariant masses in the range 1.1 GeV/c2 to 1.8 GeV/c2 are used in the "KSπ0γ (not K*(892)γ)" analysis.
We quote two averages: one for K*(892) only, and the other one for the inclusive KSπ0γ decay (including the K*(892)). If the Standard Model dipole operator is dominant, both should give the same quantities (the latter naturally with smaller statistical error). If not, care needs to be taken in interpretation of the inclusive parameters; while the results on the K*(892) resonance remain relatively clean.
At present we do not apply a rescaling of the results to a common, updated set of input parameters.
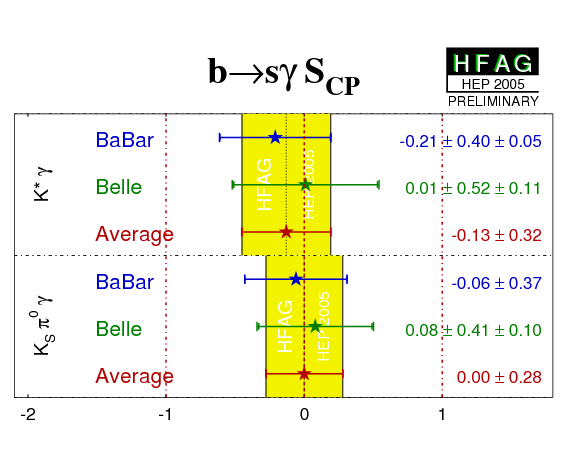
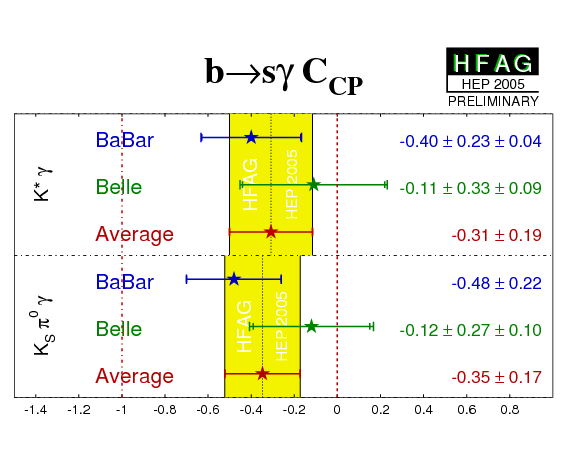
| Mode | Experiment | SKsπ0γ | CKsπ0γ = −AKsπ0γ | Correlation | Ref. / Comments |
|---|---|---|---|---|---|
| K*(892)γ |
BABAR'05
N(BB)=232m |
−0.21 ± 0.40 ± 0.05 | −0.40 ± 0.23 ± 0.04 | −0.064 | PRD 72 (2005) 051103 |
|
Belle'05
N(BB)=386m |
0.01 ± 0.52 ± 0.11 | −0.11 ± 0.33 ± 0.09 | 0.002 | BELLE-CONF-0570 (hep-ex/0507059) | |
| Average | −0.13 ± 0.32 CL=0.74 (0.3σ) |
−0.31 ± 0.19 CL=0.48 (0.7σ) |
- | uncorrelated average | |
|
KSπ0γ
(incl. K*γ) |
BABAR'05
N(BB)=232m |
−0.06 ± 0.37 | −0.48 ± 0.22 | −0.066 | PRD 72 (2005) 051103 |
|
Belle'05
N(BB)=386m |
0.08 ± 0.41 ± 0.10 | −0.12 ± 0.27 ± 0.10 | 0.004 | BELLE-CONF-0570 (hep-ex/0507059) | |
| Average | 0.00 ± 0.28 CL=0.80 (0.3σ) |
−0.35 ± 0.17 CL=0.32 (1.0σ) |
- | uncorrelated average | |
|
|
eps png K*γ only: eps png KSπ0 only: eps png |
eps png K*γ only: eps png KSπ0 only: eps png |
|||
Please note that at present we do not apply a rescaling of the results to a common, updated set of input parameters. Correlation due to common systematics are neglected in the following averages. We recall that we do NOT rescale (inflate) the errors due to measurement inconsistencies.
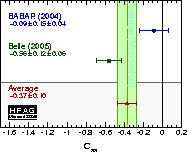
| Experiment | Sππ | Cππ = −Aππ | Correlation | Ref. / Comments | |
|---|---|---|---|---|---|
|
BABAR'04
N(BB)=227m |
−0.30 ± 0.17 ± 0.03 | −0.09 ± 0.15 ± 0.04 | −0.016 | PRL 95 (2005) 151803 | |
|
Belle'05
N(BB)=275m |
−0.67 ± 0.16 ± 0.06 | −0.56 ± 0.12 ± 0.06 | −0.09 | PRL 95 (2005) 101801 | |
| Average | −0.50 ± 0.12 | −0.37 ± 0.10 | −0.056 | χ2 = 7.9 (CL=0.019 ⇒ 2.3σ) | |
|
|

eps gif gif (high res) |
eps gif gif (high res) |
|||
Digression and plots:
The following numerical exercises involve the SU(2) and SU(3) partners of the Bd→ π+π− decay. The relevant branching ratios and CP-violating charge asymmetries are taken from HFAG - Rare Decays.
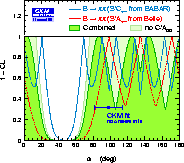
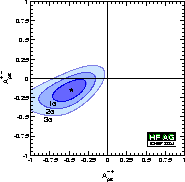
| Constraining α ≡ φ2: using as input the measured Cππ and Sππ coefficients together with the present (HFAG) ππ branching fractions and CP asymmetries (including the direct CP-asymmetry measurement for B0→ π0π0), one can perform the Gronau-London isospin analysis. The plot on the right hand side uses the statistical interpretation of the CKMfitter analysis (Rfit) (see the UTfit pages for a Bayesian interpretation). Here, it does not include the Fiertz treatment of electroweak penguins for ππ. Including it would lead to a shift in α ≡ φ2 of approximately −2 deg. All other SU(2)-breaking effects are also neglected. |
eps gif gif (high res) |
The Penguin-to-tree ratio:
using as input the measured
Cππ and Sππ coefficients
together with the Wolfenstein parameters ρ and η
from the Global CKM fit using standard constraints,
one can infer module and phase of the complex penguin
to tree (P/T) ratio
in Bd→ π+π−
decays within the Standard Model.
Note that the definition of P/T is convention-dependent
(see, e.g.,
GroRos02).
One can choose to eliminate the charm quark in
the penguin loop using CKM unitarity, so that the amplitudes are
parameterized as follows:
|
||||||||
The "Quasi-two-body" (Q2B)
CP(t) analysis of Bd→ ρ+−π−+ decays
(performed by Belle) assumes a narrow width approximation for the ρ meson.
The interference regions in the π+π−π0
Dalitz plot are removed by kinematic cuts.
Dilution of the CP results
due to residual interference effects is not accounted
for in the systematic errors.
The Q2B analysis involves 5 different parameters, one of which
− the charge asymmetry ACP(ρπ) − is time-independent.
The time-dependent decay rate is given by
Γ( B → ρ+−π−+ (Δt) )
= (1 +− ACP(ρπ)) e−|Δt|/τ/8τ
× [1 + Qtag(Sρπ+−ΔSρπ)sin(ΔmΔt)
− Qtag(Cρπ+−ΔCρπ)cos(ΔmΔt)],
where Qtag=+1(−1) when the tagging meson is a
B0 (B0-bar).
CP symmetry is violated if either one of the following conditions is true:
ACP(ρπ)≠0, Cρπ≠0 or Sρπ≠0.
The first two correspond to CP violation in the decay, while the last
condition is CP violation in the interference of decay amplitudes
with and without Bd mixing. Note that the BABAR analysis
uses a full Dalitz plot approach and hence avoids the systematic effects
due to the Q2B approximation.
At present we do not apply a rescaling of the results due to the fit dependence on the Bd lifetime and oscillation frequency.
| Experiment | ACP(ρπ) | Sρπ | Cρπ | ΔSρπ | ΔCρπ | Correlations | Ref. / Comments |
|---|---|---|---|---|---|---|---|
|
BABAR'04
N(BB)=213m |
−0.088 ± 0.049 ± 0.013 | −0.10 ± 0.14 ± 0.04 | 0.34 ± 0.11 ± 0.05 | 0.22 ± 0.15 ± 0.03 | 0.15 ± 0.11 ± 0.03 | Table | BABAR-CONF-04/038, hep-ex/0408099 |
|
Belle'04
N(BB)=152m |
−0.16 ± 0.10 ± 0.02 | −0.28 ± 0.23 +0.10−0.08 | 0.25 ± 0.17 +0.02−0.06 | −0.30 ± 0.24 ± 0.09 | 0.38 ± 0.18 +0.02−0.04 | Table | PRL 94 (2005) 121801 |
| Average | −0.102 ± 0.045 | −0.13 ± 0.13 | 0.31 ± 0.10 | 0.09 ± 0.13 | 0.22 ± 0.10 | Table | |
| Significance of CPV in the decay: Δχ2 = χ2(Acp=C=0) − χ2 = 14.5 (CL = 0.00070, that is: 3.4σ) | |||||||
Digression and plots:
|
CP violation in the decay:
as shown by
Charles
it is convenient to transform the experimentally motivated
CP parameters ACP(ρπ) and Cρπ
into the physically motivated ones
Taking into account experimental
correlations,
one finds
|
eps gif gif (high res) |
||||||||||||||||||||
|
Flavour-charge specific branching fractions:
|
|||||||||||||||||||||
The BABAR Collaboration has performed a full time-dependent Dalitz plot analysis of the decay Bd → (ρπ)0 → π+π−π0, which allows to simultaneously determine the complex decay amplitudes and the CP-violating weak phase α ≡ φ2. The analysis follows the idea of Snyder and Quinn (1993). BABAR uses a model that consists of charged and neutral ρ(770) resonances and their radial excitations ρ(1450) and ρ(1700). No non-resonant contributions are found. BABAR determines 16 coefficients of the form factor bilinears from the fit to data. The unknown amplitude parameters, among which are the phases δ+−=arg[A−+A+−*] and the UT angle α ≡ φ2, are determined from a subsequent fit to the 16 bilinear coefficients.
| Experiment | α ≡ φ2 (°) | δ+− (°) | Ref. / Comments | |
|---|---|---|---|---|
|
BABAR'04
N(BB)=213m |
113 +27−17 ± 6 | −67 +28−31 ± 7 | BABAR-CONF-04/038, hep-ex/0408099 | |
| Belle | NOT YET AVAILABLE | - | ||
| Confidence levels for α ≡ φ2 (left hand plot) and δ+− (right hand plot) as found by BABAR |

eps gif gif (high res) |
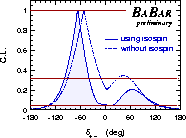
eps gif gif (high res) |
||
Note that Dalitz plot phases are non-Gaussian quantities in general. Only marginal constraints are obtained beyond 2σ.
The vector particles in the pseudoscalar to vector-vector decay Bd → ρ+ρ− can have longitudinal and transverse relative polarization with different CP properties. The BABAR Collaboration determines the fraction of longitudinally polarized events with an angular analysis to be flong = 0.978 ± 0.014+0.021−0.029, so that a per-event transversity analysis can be avoided and only the longitudinal CP parameters are determined. The Belle Collaboration determine the same quantity to be flong = 0.941 +0.034−0.040 ±0.030
At present we do not apply a rescaling of the results to a common, updated set of input parameters.
| Experiment | Sρρ,long | Cρρ,long | Correlation | Ref. / Comments |
|---|---|---|---|---|
|
BABAR'05
N(BB)=232m |
−0.33 ± 0.24 +0.08−0.14
flong = 0.978 ± 0.014+0.021−0.029 |
−0.03 ± 0.18 ± 0.09 | −0.042 | PRL 95 (2005) 041805 |
|
Belle'06
N(BB)=275m |
0.08 ± 0.41 ± 0.09
flong = 0.941 +0.034−0.040 ± 0.030 |
0.00 ± 0.30 ± 0.09 | 0.06 | PRL 96 (2006) 171801 |
| Average | −0.21 ± 0.22 | −0.03 ± 0.17 | 0.01 |
Digression and plots:
The following numerical exercises involve the SU(2) partners of the Bd → ρ+ρ− decay. The relevant branching ratios, CP-violating charge asymmetries and fractions of longitudinal polarization are taken from HFAG - Rare Decays averages.
|
Constraining α ≡ φ2:
Using as input the measured Cρρ,long and Sρρ,long coefficients together with the average (HFAG) ρρ branching fractions and longitudinal polarization fractions (including the limit on ρ0ρ0, for which the polarization is unknown), one can perform the Gronau-London isospin analysis (electroweak penguins can be taken into account, while other SU(2)-breaking effects are usually neglected). Plots for confidence level representations of the P/T phase versus its module can be found on the corresponding CKMfitter and UTfit pages. |
|
The Penguin-to-tree ratio:
Using as input the measured Cρρ,long and Sρρ,long coefficients together with the Wolfenstein parameters ρ and η using standard constraints, one can infer module and phase of the complex penguin to tree (P/T) ratio as done in the ππ case. Plots for confidence level representations of the P/T phase versus its module can be found on the corresponding CKMfitter and UTfit pages. |
|
Combined α ≡ φ2
constraint from b → uu-bar d transitions:
Averaging the confidence level curves from the ππ and ρρ isospin analyses as well as the ρπ Dalitz plot analysis, leads to the combined constraint: |

eps gif |
Neutral B meson decays such as Bd → D+−π−+, Bd → D*+−π−+ and Bd → D+−ρ−+ provide sensitivity to γ ≡ φ3 because of the interference between the Cabibbo-favoured amplitude (e.g. B0 → D−π+) with the doubly Cabibbo-suppressed amplitude (e.g. B0 → D+π−). The relative weak phase between these two amplitudes is −γ ≡ −φ3 and, when combined with the BdBd-bar mixing phase, the total phase difference is −(2β+γ) ≡ −(2φ1+φ3).
The size of the CP violating effect in each mode depends on the ratio of magnitudes of the suppressed and favoured amplitudes, e.g., rDπ = |A(B0 → D+π−)/A(B0 → D−π+)|. Each of the ratios rDπ, rD*π and rDρ is expected to be about 0.02, and can be obtained experimentally from the corresponding suppressed charged B decays, (e.g., B+ → D+π0) using isospin, or from self-tagging decays with strangeness (e.g., B0 → Ds+π−), using SU(3). In the latter case, the theoretical uncertainties are hard to quantify. The smallness of the r values makes direct extractions from, e.g., the D+−π−+ system very difficult.
Both BABAR and Belle exploit partial reconstructions of D*+−π−+ to increase the available statistics. Both experiments also reconstruct D+−π−+ and D*+−π−+ fully, and BABAR includes the mode D+−ρ−+. Additional states with similar quark content are also possible, but for vector-vector final states an angular analysis is required, while states containing higher resonances may suffer from uncertainties due to nonresonant or other contributions.
BABAR and Belle use different observables:
Here we convert the Belle results to express them in terms of a and c. Explicitly, the conversion reads:
| Belle D*π (partial reconstruction): | aπ* = − (S+ + S−)/2 |
| cπ* = − (S+ − S−)/2 | |
| Belle D*π (full reconstruction): | aπ* = + ( 2 RD*π sin( 2φ1+φ3 + δD*π ) + 2 RD*π sin( 2φ1+φ3 − δD*π ) )/2 |
| cπ* = + ( 2 RD*π sin( 2φ1+φ3 + δD*π ) − 2 RD*π sin( 2φ1+φ3 − δD*π ) )/2 | |
| Belle Dπ (full reconstruction): | aπ = − ( 2 RDπ sin( 2φ1+φ3 + δDπ ) + 2 RDπ sin( 2φ1+φ3 − δDπ ) )/2 |
| cπ = − ( 2 RDπ sin( 2φ1+φ3 + δDπ ) − 2 RDπ sin( 2φ1+φ3 − δDπ ) )/2 |
At present we do not rescale the results to a common set of input parameters. Also, common systematic errors are not considered.
| Observable | BABAR | Belle | Average | Ref. / Comments | ||
|---|---|---|---|---|---|---|
|
partially reconstructed N(BB)=232m |
fully reconstructed N(BB)=232m |
partially reconstructed N(BB)=386m |
fully reconstructed N(BB)=386m |
|||
| aD*π | −0.034 ± 0.014 ± 0.009 | −0.040 ± 0.023 ± 0.010 | −0.041 ± 0.019 ± 0.017 | −0.039 ± 0.020 ± 0.013 | −0.037 ± 0.011
CL=0.96 (0.0σ) |
BABAR: PRD 71 (2005) 112003 (partially reco.) BABAR-PUB-06/001 (hep-ex/0602049) (fully reco.) Belle: PRD 73, 092003 (2006) |
| - | COMBINED: −0.040 ± 0.014 ± 0.011 | |||||
| cD*π | −0.019 ± 0.022 ± 0.013
(lepton tags only) |
0.049 ± 0.042 ± 0.015
(lepton tags only) |
−0.007 ± 0.019 ± 0.017 | −0.011 ± 0.020 ± 0.013 | −0.006 ± 0.014 CL=0.41 (0.8σ) |
|
| - | COMBINED: −0.009 ± 0.014 ± 0.011 | |||||
| aDπ | - | −0.010 ± 0.023 ± 0.007 | - | −0.050 ± 0.021 ± 0.012 | −0.030 ± 0.017
CL=0.24 (1.2σ) |
|
| cDπ | - | −0.033 ± 0.042 ± 0.012
(lepton tags only) |
- | −0.019 ± 0.021 ± 0.012 | −0.022 ± 0.021
CL=0.78 (0.3σ) |
|
| aDρ | - | −0.024 ± 0.031 ± 0.009 | - | - | −0.024 ± 0.033 | |
| cDρ | - | −0.098 ± 0.055 ± 0.018
(lepton tags only) |
- | - | −0.098 ± 0.058 | |
| Compilation of the above results. |
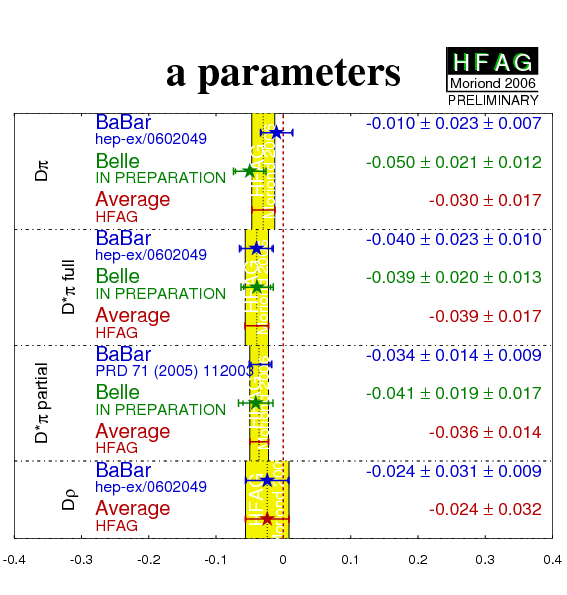
eps.gz png |
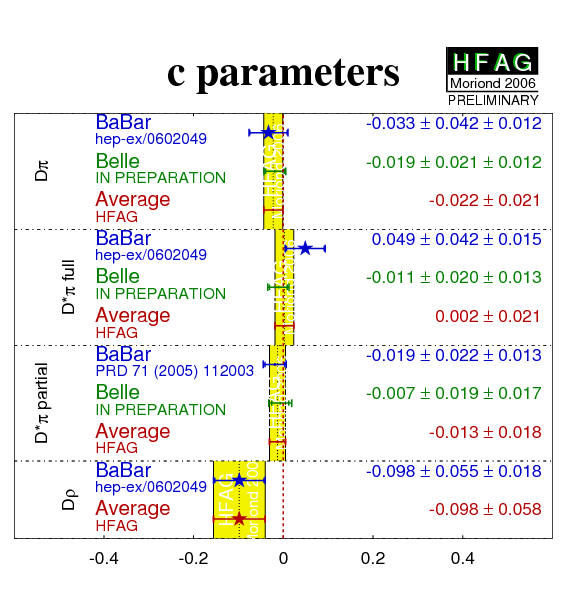
eps.gz png |
| Averages of the D*π results. |
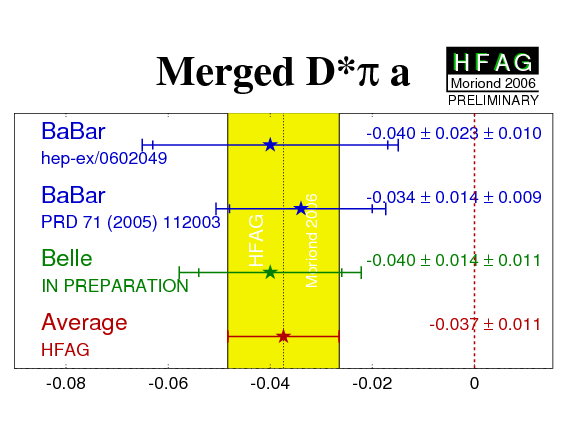
eps.gz png |
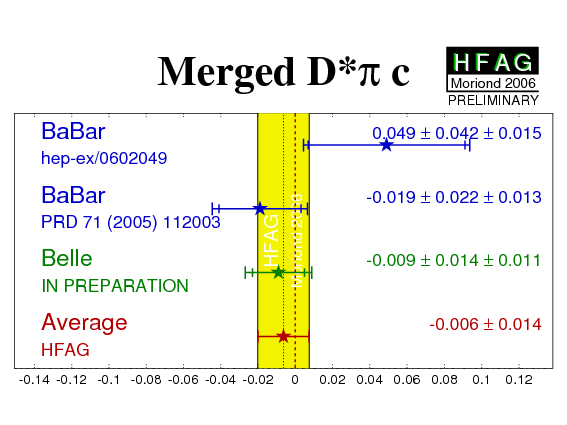
eps.gz png |
Digression:
|
Constraining 2β+γ ≡
2φ1+φ3:
The constraints can be tightened if one is willing to use theoretical input on the values of R and/or δ. One popular choice is the use of SU(3) symmetry to obtain R by relating the suppressed decay mode to B decays involving Ds mesons. For more information, visit the CKMfitter and UTfit sites. |
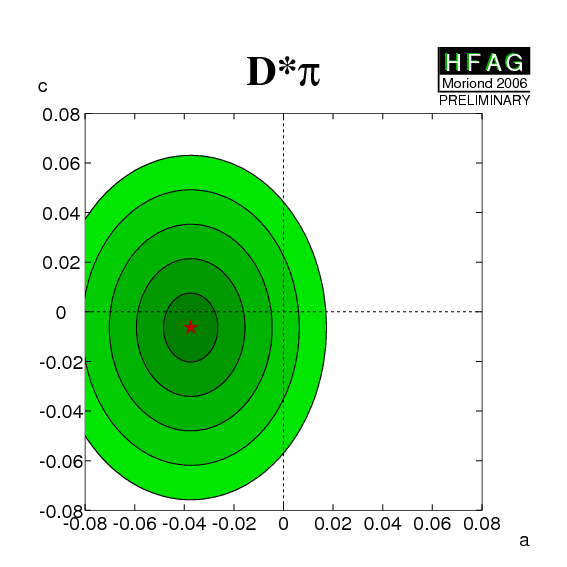
eps.gz png |
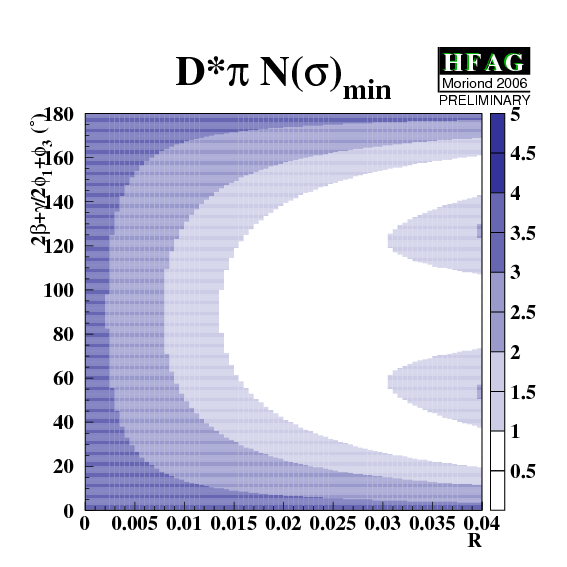
eps.gz png CL: eps.gz png |
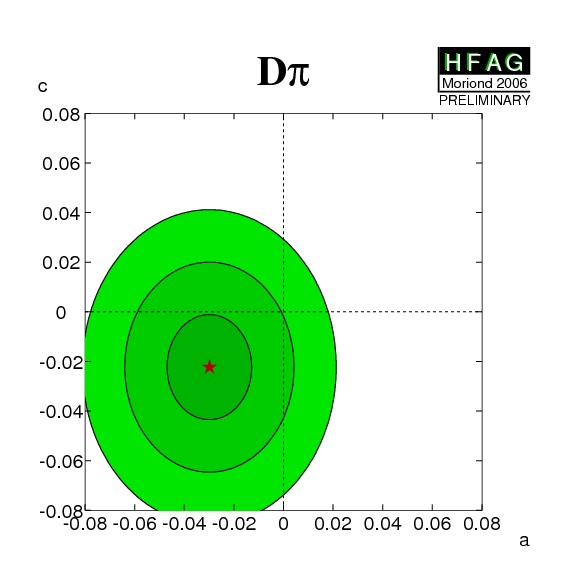
eps.gz png |
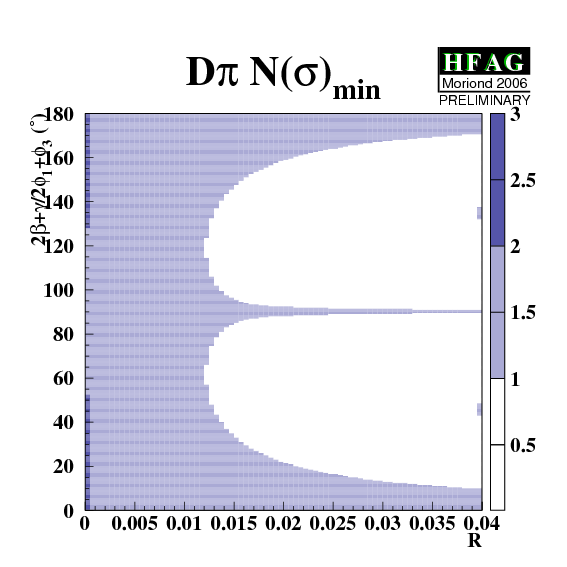
eps.gz png CL: eps.gz png |
A theoretically clean measurement of the angle γ ≡ φ3 can be obtained from the rate and asymmetry measurements of B− → D(*)CPK(*)− decays, where the D(*) meson decays to CP even (D(*)CP+) and CP odd (D(*)CP−) eigenstates. The method benefits from the interference between the dominant b→cu-bar s transitions with the corresponding doubly CKM-suppressed b→uc-bar s transition. It was proposed by Gronau, Wyler and Gronau, London (GLW).
BABAR and Belle use consistent definitions for ACP+− and RCP+−, where
| ACP+− = [Γ(B− → D(*)CP+−K(*)−) − Γ(B+ → D(*)CP+−K(*)+)] / Sum , |
| RCP+− = [Γ(B− → D(*)CP+−K(*)−) + Γ(B+ → D(*)CP+−K(*)+)] / [Γ(B− → D(*)0 K(*)−) + Γ(B+ → D(*)0-bar K(*)+)]. |
Experimentally, it is convenient to measure RCP+− using double ratios, in which similar ratios for B− → D(*) π(*)− decays are used for normalization.
These observables have been measured so far for three D(*)K(*)− modes. Both Belle and BABAR use the CP even D decays to K+K− and π+π− in all three modes; both experiments also use only the D* → Dπ0 decay, which gives CP(D*) = CP(D). For CP-odd D decay modes, Belle use KSπ0, KSφ and KSω in all three analyses, and also use KSη in DK− and D*K− analyses. BABAR use KSπ0, KSφ and KSω for DK− analysis.
At present we do not rescale the results to a common set of input parameters. Also, common systematic errors are not considered.
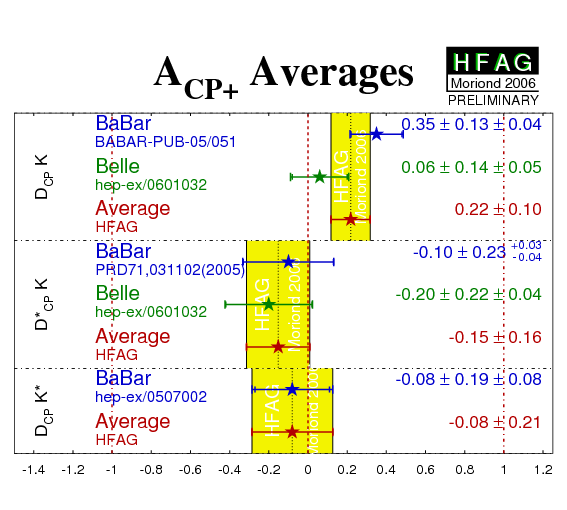
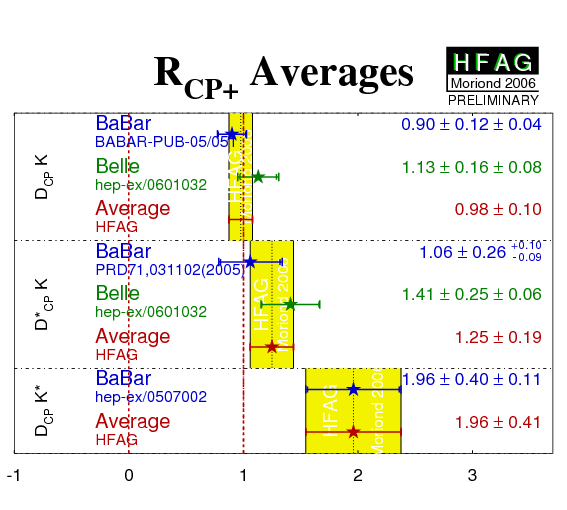
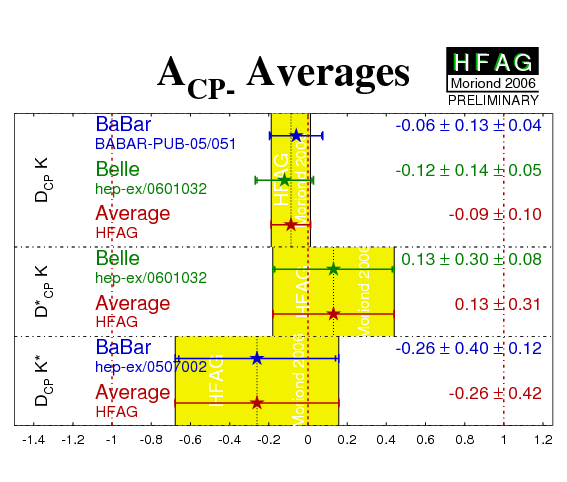
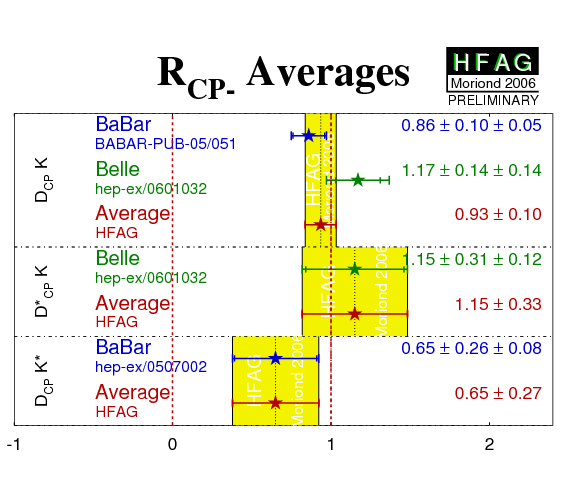
| Mode | Experiment | ACP+ | ACP− | RCP+ | RCP− | Ref. / Comments |
|---|---|---|---|---|---|---|
| DCPK− |
BABAR'05
N(BB)=232m |
0.35 ± 0.13 ± 0.04 | −0.06 ± 0.13 ± 0.04 | 0.90 ± 0.12 ± 0.04 | 0.86 ± 0.10 ± 0.05 | PRD 73, 051105 (2006) |
|
Belle'06
N(BB)=275m |
0.06 ± 0.14 ± 0.05 | −0.12 ± 0.14 ± 0.05 | 1.13 ± 0.16 ± 0.08 | 1.17 ± 0.14 ± 0.14 | PRD 73, 051106 (2006) | |
| Average | 0.22 ± 0.10 | −0.09 ± 0.10 | 0.98 ± 0.10 | 0.94 ± 0.10 | ||
| D*CPK− |
BABAR'04
N(BB)=123m |
−0.10 ± 0.23 +0.03−0.04 | - | 1.06 ± 0.26 +0.10−0.09 | - | PRD 71 (2005) 031102 |
|
Belle'06
N(BB)=275m |
−0.20 ± 0.22 ± 0.04 | 0.13 ± 0.30 ± 0.08 | 1.41 ± 0.25 ± 0.06 | 1.15 ± 0.31 ± 0.12 | PRD 73, 051106 (2006) | |
| Average | −0.15 ± 0.16 | 0.13 ± 0.31 | 1.25 ± 0.19 | 1.15 ± 0.33 | ||
| DCPK*− |
BABAR'05
N(BB)=232m |
−0.08 ± 0.19 ± 0.08 | −0.26 ± 0.40 ± 0.12 | 1.96 ± 0.40 ± 0.11 | 0.65 ± 0.26 ± 0.08 | PRD 72 (2005) 071103(R) |
| Belle | NO RESULTS AVAILABLE (*) | - | ||||
| Average | −0.08 ± 0.21 | −0.26 ± 0.42 | 1.96 ± 0.41 | 0.65 ± 0.27 | ||
| Compilation of the above results. |
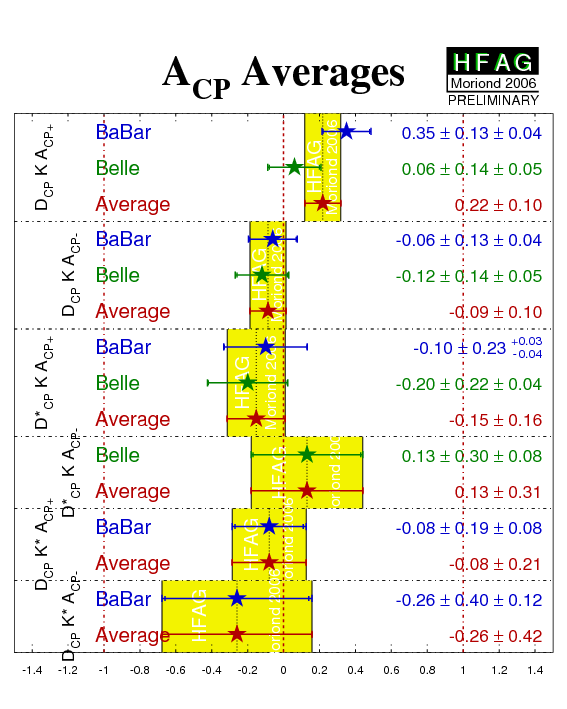
eps.gz png |
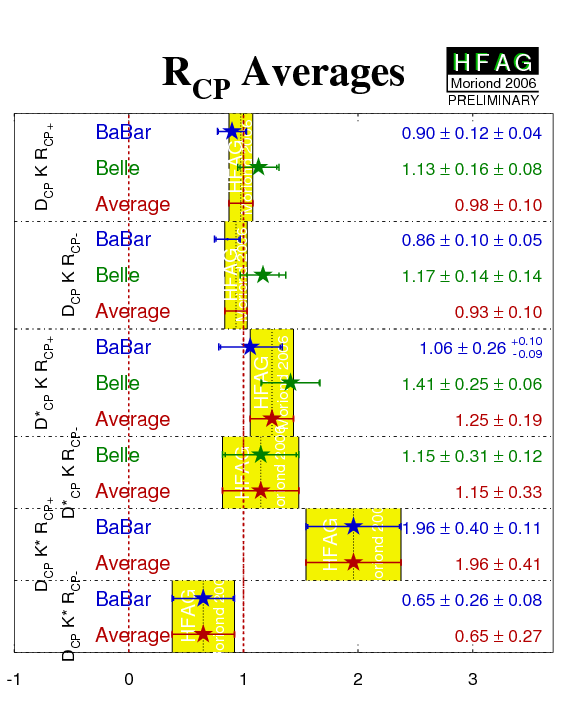
eps.gz png |
| CP+ only |
eps.gz png |
eps.gz png |
| CP- only |
eps.gz png |
eps.gz png |
Digression:
Constraining γ ≡ φ3:
The rate ratios and asymmetries of the GLW method can be
expressed in terms of amplitude ratios and strong phase differences,
as well as the weak phase difference γ ≡ φ3.
For the GLW observables, one has:
where rB = |A(b→u)/A(b→c)| and δB = arg[A(b→u)/A(b→c)]. Only the weak phase difference γ ≡ φ3 is universal, while the other parameters depend on the decay process. Plots upcoming. |
A modification of the GLW idea has been suggested by Atwood, Dunietz and Soni, where B− → DK− with D → K+π− (or similar) and the charge conjugate decays are used. Here, the favoured (b→c) B decay followed by the doubly CKM-suppressed D decay interferes with the suppressed (b→u) B decay followed by the CKM-favored D decay. The relative similarity of the combined decay amplitudes enhances the possible CP asymmetry. BABAR and Belle use consistent definitions for AKπ and RKπ, where
| AKπ = [Γ(B− → [K+π−]D(*)K(*)−) − Γ(B+ → [K−π+]D(*)K(*)+)] / [Γ(B− → [K+π−]D(*)K(*)−) + Γ(B+ → [K−π+]D(*)K(*)+)] , |
| RKπ = [Γ(B− → [K+π−]D(*)K(*)−) + Γ(B+ → [K−π+]D(*)K(*)+)] / [Γ(B− → [K−π+]D(*)K(*)−) + Γ(B+ → [K+π−]D(*)K(*)+)] . |
(Some of) these observables have been measured so far for the D(*)K− modes.
At present we do not rescale the results to a common set of input parameters. Also, common systematic errors are not considered.
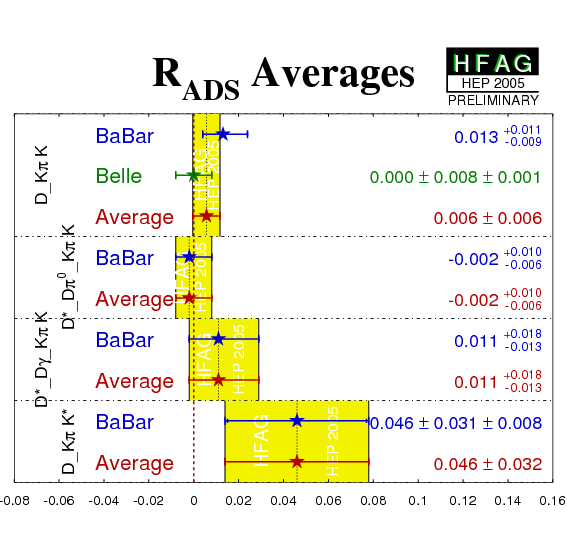
| Mode | Experiment | AKπ | RKπ | Ref. / Comments |
|---|---|---|---|---|
|
DK−
D→Kπ |
BABAR'05
N(BB)=232m |
- | 0.013 +0.011−0.009 | PRD 72 (2005) 032004 |
|
Belle'05
N(BB)=386m |
- | 0.000 ± 0.008 ± 0.001 | BELLE-CONF-0552 (hep-ex/0508048) | |
| Average | - | 0.006 ± 0.006 | ||
|
D*K−
D* → Dπ0 D→Kπ |
BABAR'05
N(BB)=232m |
- | −0.002+0.010−0.006 | PRD 72 (2005) 032004 |
| Average | - | −0.002+0.010−0.006 | ||
|
D*K−
D* → Dγ D→Kπ |
BABAR'05
N(BB)=232m |
- | 0.011+0.018−0.013 | PRD 72 (2005) 032004 |
| Average | - | 0.011+0.018−0.013 | ||
|
DK*−
D→Kπ |
BABAR'05
N(BB)=232m |
−0.22 ± 0.61 ± 0.17 | 0.046 ± 0.031 ± 0.008 | BABAR-PUB-05/039 (hep-ex/0508001) |
| Average | −0.22 ± 0.63 | 0.046 ± 0.032 |
| Compilation of the above results. |
eps.gz png |
Digression:
|
Constraining γ ≡ φ3: As for the GLW method, the rate ratios and asymmetries of the ADS method can be expressed in terms of amplitude ratios and strong phase differences, as well as the weak phase difference γ ≡ φ3. For the ADS observables, one has:
where rB = |A(b→u)/A(b→c)| and δB = arg[A(b→u)/A(b→c)] as before. rD and δD are the corresponding amplitude ratio and strong phase difference of the D meson decay amplitudes. The value of rD2 is obtained from the ratio of the suppressed-to-allowed branching fractions BR(D0 → K+π−) = (1.38 ± 0.11)×10−4 and BR(D0 → K−π+) = (3.80 ± 0.09)×10−2 [PDG 2004], respectively. With this it is found rD = 0.0603 ± 0.0025. The strong phase is different, in general, for D and D* mesons. Bondar and Gershon have pointed out that there is an effective strong phase shift of π between the cases that D* is reconstructed in the Dπ0 and Dγ final states, which in principle allows γ ≡ φ3 to be measured using the ADS technique with B+− → D* K+− alone. Plots upcoming. |
As can be seen from the expressions above, the maximum size of the asymmetry, for given values of rB and rD is given by: AKπ (max) = 2rBrD / (rB2+rD2). Thus, sizeable asymmetries may be found also for B− → D(*)π− decays, despite the expected smallness (~0.01) of rB for this case, providing sensitivity to γ ≡ φ3. The observables have been measured by Belle in the Dπ− mode.
| Mode | Experiment | AKπ | RKπ | Ref. / Comments |
|---|---|---|---|---|
|
Dπ−
D→Kπ |
Belle'05
N(BB)=386m |
0.10 ± 0.22 ± 0.06 | 0.0035 +0.0008−0.0007 ± 0.0003 | BELLE-CONF-0552 (hep-ex/0508048) |
| Average | 0.10 ± 0.23 | 0.0035 +0.0009−0.0008 |
Another method to extract γ ≡ φ3 from the interference between B− → D(*)0 K− and B− → D(*)0-bar K− uses multibody D decays. A Dalitz plot analysis allows simultaneous determination of the weak phase difference γ ≡ φ3, the strong phase difference δB and the ratio of amplitudes rB. This idea was proposed by Giri, Grossman, Soffer and Zupan and the Belle Collaboration. The assumption of a D decay model results in an additional model uncertainty.
Results are available from both Belle and BABAR using B− → D K−, B− → D*K− and B− → DK*−. Belle use the D* decay to Dπ0 only, while BABAR also use Dγ, and take the effective strong phase shift into account. In all cases the decay D → KSπ+π− is used.
For the DK*− mode, both collaborations use K*− → KSπ−; in this case some care is needed due to other possible contributions to the B− → DKSπ− final state. Belle assign an additional (model) uncertainty, while BABAR use an alternative parametrization [replacing rB and δB with κrs and δs, respectively] suggested by Gronau. Due to these different treatments, the averages for this mode should be treated with care.
If the values of γ ≡ φ3, δB and rB are obtained by directly fitting the data, the extracted value of rB is biased (since it is positive definite by nature). Since the error on γ ≡ φ3 depends on the value of rB some statistical treatment is necessary to correctly estimate the uncertainty. To obviate this effect, both experiments now use a different set of variables in the fits:
| x+ = rB cos( δB+γ ) ≡ rB cos( δB+φ3 ) | y+ = rB sin( δB+γ ) ≡ rB sin( δB+φ3 ) |
| x− = rB cos( δB−γ ) ≡ rB cos( δB−φ3 ) | y− = rB sin( δB−γ ) ≡ rB sin( δB−φ3 ) |
These parameters have the advantage of having (approximately) Gaussian distributions, and of having small statistical correlations. Some statistical treatment is necessary to convert these measurements into constraints on the underlying physical parameters γ ≡ φ3, δB and rB [BaBar do not obtain constraints on rB and δB for the B− → DK*− decay due to the reparametrization described above]. Both experiments use frequentist procedures, though there are differences in the details.
The results below have three sets of errors, which are statistical, systematic, and model related uncertainties respectively. Note that the Belle results for (x+, y+, x−, y−) do not include model uncertainty. (See Appendix of Ref.) Since the model uncertainty should be 100% correlated between experiments, we average the values of (x+, y+, x−, y−) without including this source of error, and then add it back on to the averaged values.
| Mode | Experiment | x+ | y+ | x− | y− | Correlations | Ref. / Comments |
|---|---|---|---|---|---|---|---|
|
DK−
D→KSπ+π− |
BABAR'05
N(BB)=227m |
−0.13 ± 0.07 ± 0.03 ± 0.03 | 0.02 ± 0.08 ± 0.02 ± 0.02 | 0.08 ± 0.07 ± 0.03 ± 0.02 | 0.06 ± 0.09 ± 0.04 ± 0.04 | - |
BABAR:
PRL 95, 121802 (2005); BABAR-CONF-05/018 (hep-ex/0507101) Belle: hep-ex/0604054 (submitted to PRD) |
|
Belle'06
N(BB)=386m |
−0.14 ± 0.07 ± 0.02 | −0.09 ± 0.09 ± 0.01 | 0.03 +0.07−0.08 ± 0.01 | 0.17 +0.09−0.12 ± 0.02 | See Appendix of Ref. | ||
| Average | −0.14 ± 0.05 ± 0.03 | −0.03 ± 0.06 ± 0.02 | 0.05 ± 0.05 ± 0.02 | 0.11 ± 0.07 ± 0.04 | UNCORRELATED AVERAGES | ||
|
D*K−
D*→Dπ0 & D*→Dγ D→KSπ+π− |
BABAR'05
N(BB)=227m |
0.14 ± 0.09 ± 0.03 ± 0.03 | 0.01 ± 0.12 ± 0.04 ± 0.06 | −0.13 ± 0.09 ± 0.03 ± 0.02 | −0.14 ± 0.11 ± 0.02 ± 0.03 | - | |
|
Belle'06
N(BB)=386m |
0.03 ± 0.12 ± 0.01 | 0.01 ± 0.14 ± 0.01 | −0.13 +0.17−0.15 ± 0.02 | −0.34 +0.17−0.16 ± 0.03 | See Appendix of Ref. | ||
| Average | 0.10 ± 0.07 ± 0.03 | 0.01 ± 0.09 ± 0.06 | −0.13 ± 0.08 ± 0.02 | −0.20 ± 0.09 ± 0.03 | UNCORRELATED AVERAGES | ||
|
DK*−
K*− → KSπ− D→KSπ+π− |
BABAR'05
N(BB)=227m |
−0.07 ± 0.23 ± 0.13 ± 0.03 | −0.01 ± 0.32 ± 0.18 ± 0.05 | −0.20 ± 0.20 ± 0.11 ± 0.03 | 0.26 ± 0.30 ± 0.16 ± 0.03 | - | |
|
Belle'06
N(BB)=386m |
−0.11 +0.18−0.17 ± 0.01 | 0.00 ± 0.16 ± 0.01 | −0.78 +0.25−0.30 ± 0.03 | −0.28 +0.44−0.34 ± 0.05 | See Appendix of Ref. | ||
| Average | −0.10 ± 0.15 ± 0.03 | 0.00 ± 0.15 ± 0.05 | −0.46 ± 0.17 ± 0.03 | 0.05 ± 0.27 ± 0.03 | UNCORRELATED AVERAGES |
Digression:
| Constraining γ/φ3: The measurements of x+,− and y+,− in the various D(*)K(*) decay modes can be used to place bounds on γ ≡ φ3. Both experiments have done so using frequentist techniques. | |||
|
BABAR obtain
γ = (67 ± 28 ± 13 ± 11)° |
Belle obtain
φ3 = (53 +15−18 ± 3 ± 9)° |
||
| The experiments also obtain values for the hadronic parameters | |||
| rB (DK−) = 0.12 ± 0.08 ± 0.03 ± 0.04 | δ B (DK−) = (104 ± 45 +17−21 +16−24)° | rB (DK−) = 0.16 ± 0.05 ± 0.01 ± 0.05 | δ B (DK−) = (146 +19−20 ± 3 ± 23)° |
| rB (D*K−) = 0.17 ± 0.10 ± 0.03 ± 0.03 | δ B (D*K−) = (296 ± 41 +14−12 ± 15)° | rB (D*K−) = 0.18 +0.11−0.10 ± 0.01 ± 0.05 | δ B (D*K−) = (302 +34−35 ± 6 ± 23)° |
| . | . | rB (DK*−) = 0.56 +0.22−0.16 ± 0.04 ± 0.08 | δ B (DK*−) = (243+20−23 ± 3 ± 50 )° |
| Note that the above results suffer an ambiguity: γ → γ + π ≡ φ3 → φ3 + π, δ → δ + π. We quote the result which is consistent with the Standard Model fit. | |||