 Time-dependent CP violation & Unitarity Triangle angles
Time-dependent CP violation & Unitarity Triangle angles
 Time-dependent CP violation & Unitarity Triangle angles
Time-dependent CP violation & Unitarity Triangle angles
|
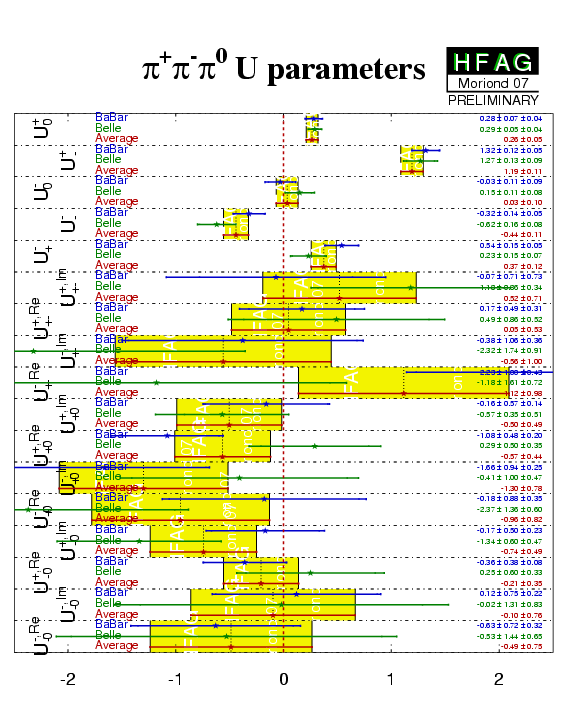
Both BaBar and Belle have performed a full time-dependent Dalitz plot analyses of the decay Bd → (ρπ)0 → π+π−π0, which allows to simultaneously determine the complex decay amplitudes and the CP-violating weak phase α ≡ φ2. The analysis follows the idea of Snyder and Quinn (1993), implemented as suggested by Quinn and Silva. The experiments determine 27 coefficients of the form factor bilinears from the fit to data. Physics parameters, such as the quasi-two-body parameters, and the phases δ+−=arg[A−+A+−*] and the UT angle α ≡ φ2, are determined from subsequent fits to the bilinear coefficients.
Please note that at present we do not apply a rescaling of the results to a common, updated set of input parameters. Correlation due to common systematics are neglected in the following averages.
| Measurement |
BaBar
N(BB)=375M |
Belle
N(BB)=449M |
Average |
|---|---|---|---|
| U+0 | 0.28 ± 0.07 ± 0.04 | 0.29 ± 0.05 ± 0.04 | 0.26 ± 0.05 |
| U+− | 1.32 ± 0.12 ± 0.05 | 1.27 ± 0.13 ± 0.09 | 1.19 ± 0.11 |
| U−0 | −0.03 ± 0.11 ± 0.09 | 0.15 ± 0.11 ± 0.08 | 0.03 ± 0.10 |
| U−− | −0.32 ± 0.14 ± 0.05 | −0.62 ± 0.16 ± 0.08 | −0.44 ± 0.11 |
| U−+ | 0.54 ± 0.15 ± 0.05 | 0.23 ± 0.15 ± 0.07 | 0.37 ± 0.12 |
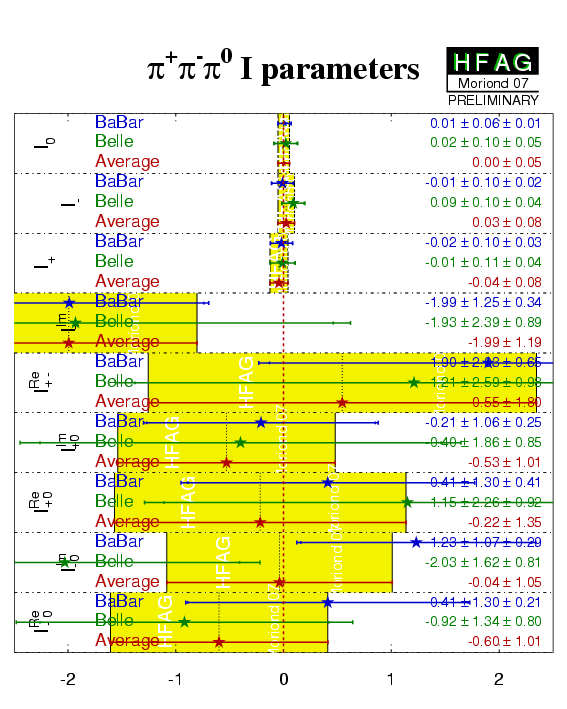
| I0 | 0.01 ± 0.06 ± 0.01 | 0.02 ± 0.10 ± 0.05 | 0.00 ± 0.05 |
| I- | −0.01 ± 0.10 ± 0.02 | 0.09 ± 0.10 ± 0.04 | 0.03 ± 0.08 |
| I+ | −0.02 ± 0.10 ± 0.03 | −0.01 ± 0.11 ± 0.04 | −0.04 ± 0.08 |
| U+,Im+− | −0.07 ± 0.71 ± 0.73 | 1.18 ± 0.86 ± 0.34 | 0.52 ± 0.71 |
| U+,Re+− | 0.17 ± 0.49 ± 0.31 | 0.49 ± 0.86 ± 0.52 | 0.05 ± 0.53 |
| U−,Im+− | −0.38 ± 1.06 ± 0.36 | −2.32 ± 1.74 ± 0.91 | −0.56 ± 1.00 |
| U−,Re+− | 2.23 ± 1.00 ± 0.43 | −1.18 ± 1.61 ± 0.72 | 1.12 ± 0.98 |
| IIm+− | −1.99 ± 1.25 ± 0.34 | −1.93 ± 2.39 ± 0.89 | −1.99 ± 1.19 |
| IRe+− | 1.90 ± 2.03 ± 0.65 | 1.21 ± 2.59 ± 0.98 | 0.55 ± 1.80 |
| U+,Im+0 | −0.16 ± 0.57 ± 0.14 | −0.57 ± 0.35 ± 0.51 | −0.50 ± 0.49 |
| U+,Re+0 | −1.08 ± 0.48 ± 0.20 | 0.29 ± 0.50 ± 0.35 | −0.57 ± 0.44 |
| U−,Im+0 | −1.66 ± 0.94 ± 0.25 | −0.41 ± 1.00 ± 0.47 | −1.30 ± 0.78 |
| U−,Re+0 | −0.18 ± 0.88 ± 0.35 | −2.37 ± 1.36 ± 0.60 | −0.96 ± 0.82 |
| IIm+0 | −0.21 ± 1.06 ± 0.25 | −0.40 ± 1.86 ± 0.85 | −0.53 ± 1.01 |
| IRe+0 | 0.41 ± 1.30 ± 0.41 | 1.15 ± 2.26 ± 0.92 | −0.22 ± 1.35 |
| U+,Im−0 | −0.17 ± 0.50 ± 0.23 | −1.34 ± 0.60 ± 0.47 | −0.74 ± 0.49 |
| U+,Re−0 | −0.36 ± 0.38 ± 0.08 | 0.25 ± 0.60 ± 0.33 | −0.21 ± 0.35 |
| U−,Im−0 | 0.12 ± 0.75 ± 0.22 | −0.02 ± 1.31 ± 0.83 | −0.10 ± 0.76 |
| U−,Re−0 | −0.63 ± 0.72 ± 0.32 | −0.53 ± 1.44 ± 0.65 | −0.49 ± 0.75 |
| IIm−0 | 1.23 ± 1.07 ± 0.29 | −2.03 ± 1.62 ± 0.81 | −0.04 ± 1.05 |
| IRe−0 | 0.41 ± 1.30 ± 0.21 | −0.92 ± 1.34 ± 0.80 | −0.60 ± 1.01 |
| Correlations | (stat) (syst) | (stat) | (stat) |
| Reference | hep-ex/0703008 | hep-ex/0701015 |
HFAG correlated average
χ2 = 19.0/26 dof (CL=0.85 ⇒ 0.2σ) |
| Compilation of averages of the form factor bilinears. |
eps.gz png |
eps.gz png |
From the bilinear coefficients given above, both experiments extract "quasi-two-body" (Q2B) parameters. Considering only the charged ρ bands in the Dalitz plot, the Q2B analysis involves 5 different parameters, one of which − the charge asymmetry ACP(ρπ) − is time-independent. The time-dependent decay rate is given by
where Qtag=+1(−1) when the tagging meson is a B0 (B0-bar). CP symmetry is violated if either one of the following conditions is true: ACP(ρπ)≠0, Cρπ≠0 or Sρπ≠0. The first two correspond to CP violation in the decay, while the last condition is CP violation in the interference of decay amplitudes with and without Bd mixing.
We average the quasi-two-body parameters provided by the experiments, which should be equivalent to determining average values directly from the averaged bilinear coefficients.
As shown by
Charles
it can be convenient to transform the experimentally motivated
CP parameters ACP(ρπ) and Cρπ
into the physically motivated choices
A+−(ρπ) =
(|κ+−|2−1)/(|κ+−|2+1) =
−(ACP(ρπ)+Cρπ+ACP(ρπ)ΔCρπ)/(1+ΔCρπ + ACP(ρπ)Cρπ),
A−+(ρπ) =
(|κ−+|2−1)/(|κ−+|2+1) =
(−ACP(ρπ)+Cρπ+ACP(ρπ)ΔCρπ)/(−1+ΔCρπ + ACP(ρπ)Cρπ),
where
κ+− = (q/p)Abar−+/A+− and
κ−+ = (q/p)Abar+−/A−+.
With this definition A−+(ρπ) (A+−(ρπ))
describes CP violation in Bd decays
where the ρ is emitted (not emitted) by the spectator interaction.
Both experiments obtain values for A+− and A−+,
which we average.
Again, this procedure should be equivalent to extracting these values
directly from the previous results.
In addition to the Bd→ ρ+−π−+ quasi-two-body contributions to the π+π−π0 final state, there can also be a Bd→ ρ0π0 component. Both experiments have also extracted the quasi-two-body parameters associated with this intermediate state.
Note again that at present we do not apply a rescaling of the results to a common, updated set of input parameters. Correlations due to possible common systematics are neglected in the following averages.
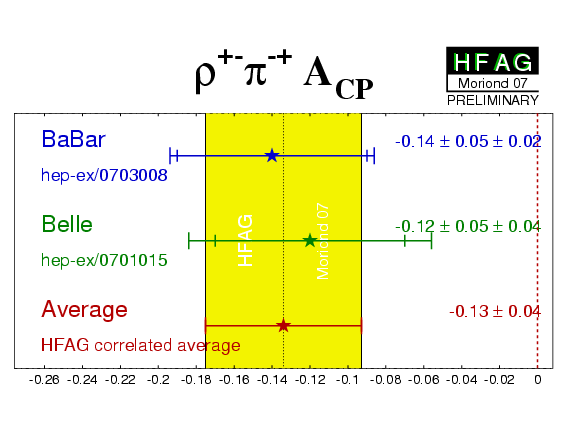
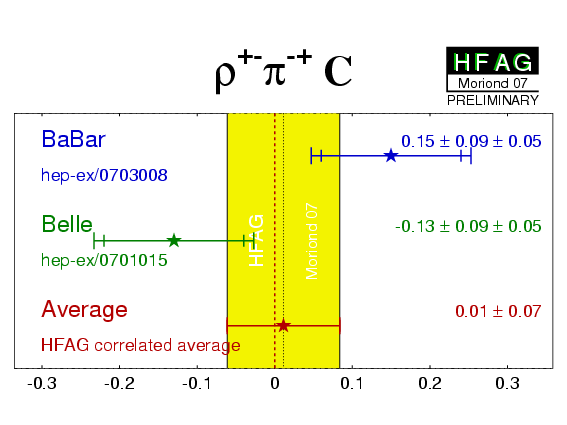
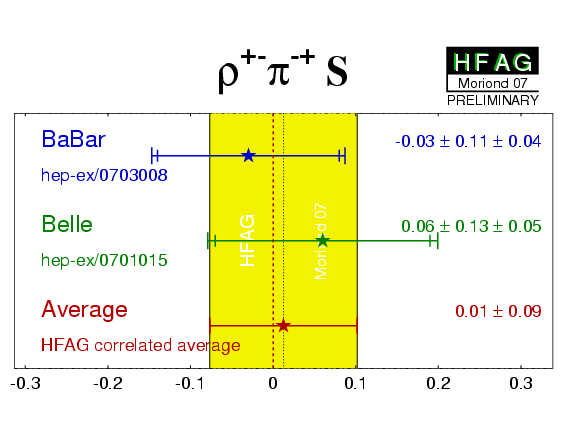
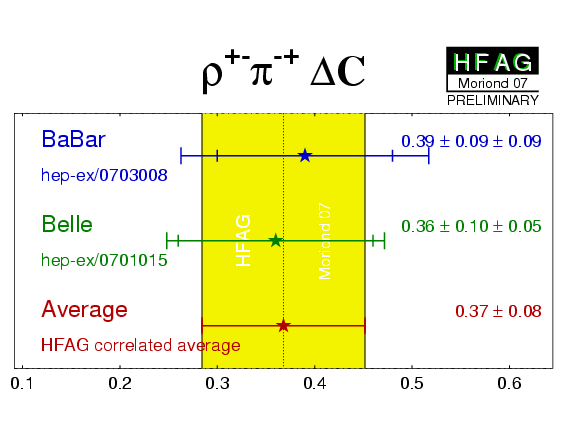
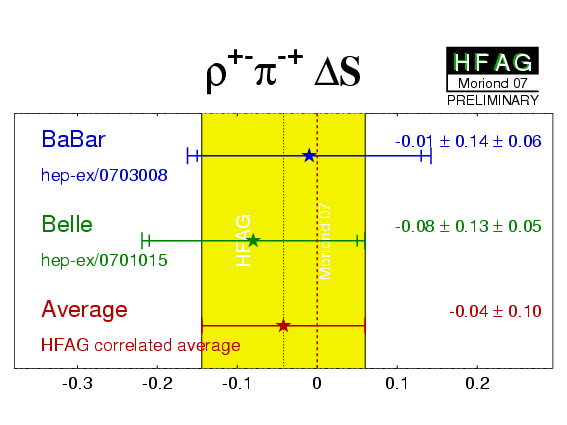
| Experiment | ACP (ρ+−π−+) | C (ρ+−π−+) | S (ρ+−π−+) | ΔC (ρ+−π−+) | ΔS (ρ+−π−+) | Correlations | Reference |
|---|---|---|---|---|---|---|---|
|
BaBar
N(BB)=375M |
−0.14 ± 0.05 ± 0.02 | 0.15 ± 0.09 ± 0.05 | −0.03 ± 0.11 ± 0.04 | 0.39 ± 0.09 ± 0.09 | −0.01 ± 0.14 ± 0.06 | (stat) | hep-ex/0703008 |
|
Belle
N(BB)=449M |
−0.12 ± 0.05 ± 0.04 | −0.13 ± 0.09 ± 0.05 | 0.06 ± 0.13 ± 0.05 | 0.36 ± 0.10 ± 0.05 | −0.08 ± 0.13 ± 0.05 | (stat) | hep-ex/0701015 |
| Average | −0.13 ± 0.04 | 0.01 ± 0.07 | 0.01 ± 0.09 | 0.37 ± 0.08 | −0.04 ± 0.10 | (stat) |
HFAG correlated average
χ2 = 4.2/5 dof (CL=0.52 ⇒ 0.6σ) |
|
|
eps.gz png |
eps.gz png |
eps.gz png |
eps.gz png |
eps.gz png |
. | |
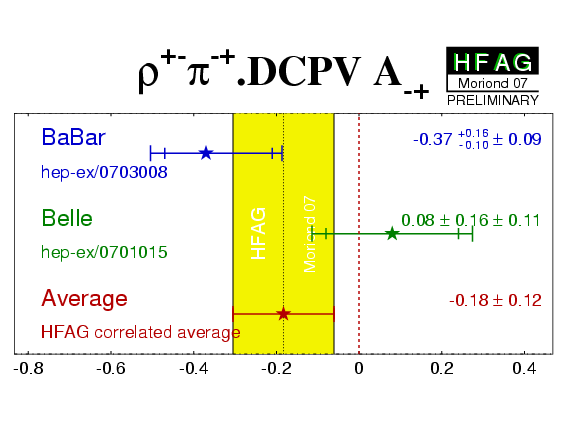
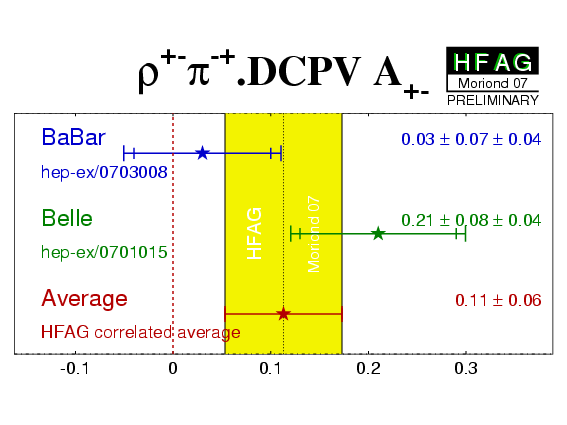
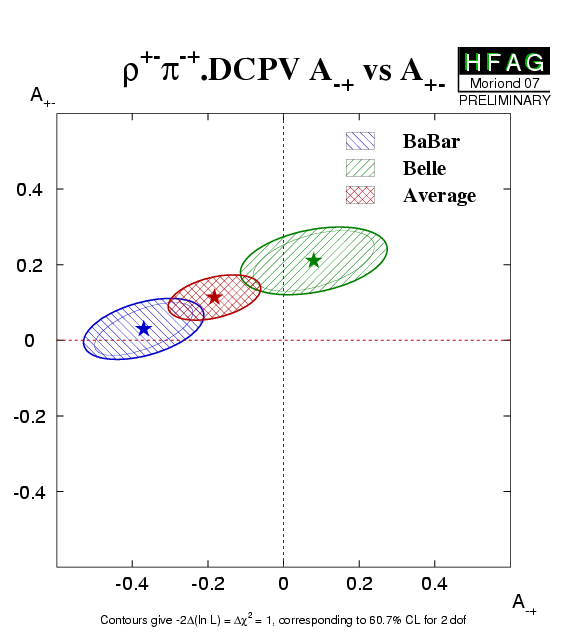
| Experiment | A−+ (ρ+−π−+) | A+− (ρ+−π−+) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=375M |
−0.37 +0.16 −0.10 ± 0.09 | 0.03 ± 0.07 ± 0.04 | 0.62 | hep-ex/0703008 |
|
Belle
N(BB)=449M |
0.08 ± 0.16 ± 0.11 | 0.21 ± 0.08 ± 0.04 | 0.47 | hep-ex/0701015 |
| Average | −0.18 ± 0.12 | 0.11 ± 0.06 | 0.40 |
HFAG correlated average
χ2 = 4.0/2 dof (CL=0.14 ⇒ 1.5σ) |
|
|
eps.gz png |
eps.gz png |
eps.gz png |
|
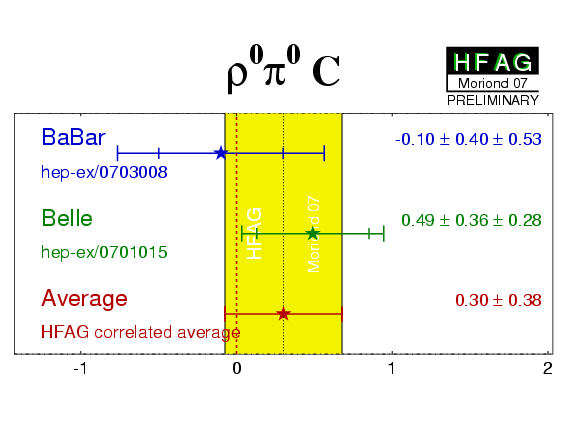
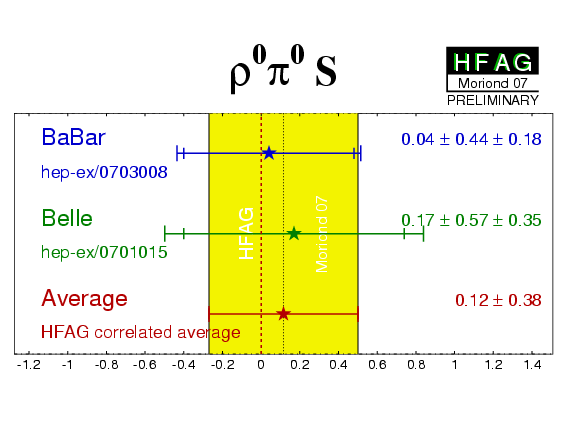
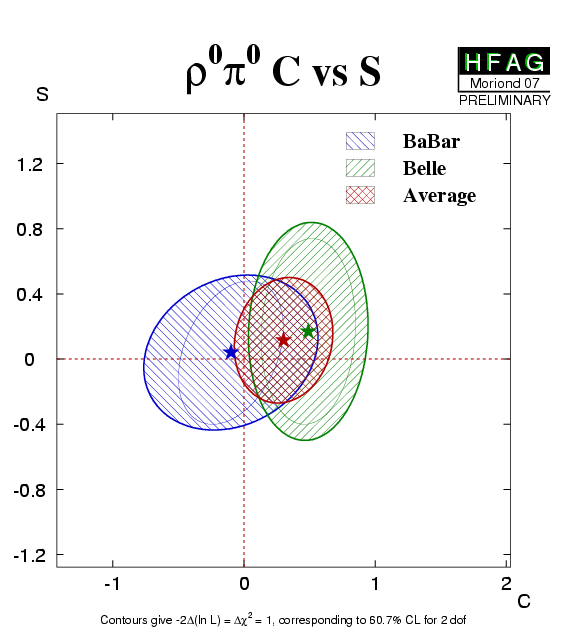
| Experiment | C (ρ0π0) | S (ρ0π0) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=375M |
−0.10 ± 0.40 ± 0.53 | 0.04 ± 0.44 ± 0.18 | 0.35 | hep-ex/0703008 |
|
Belle
N(BB)=449M |
0.49 ± 0.36 ± 0.28 | 0.17 ± 0.57 ± 0.35 | 0.08 | hep-ex/0701015 |
| Average | 0.30 ± 0.38 | 0.12 ± 0.38 | 0.12 |
HFAG correlated average
χ2 = 0.5/2 dof (CL=0.76 ⇒ 0.3σ) |
|
|
eps.gz png |
eps.gz png |
eps.gz png |
|
Interpretations:
The information given above can be used to extract α ≡ φ2.
From the measured form factor bilinears,
BaBar
extract a confidence level interpretation for α,
and constrain α = (87+45−13)° at 68% confidence level.
Belle
has performed a similar analysis.
In addition, Belle
has also included information from the SU(2) partners of B → ρπ,
which can be used to constrain α ≡ φ2 via an
isospin pentagon
relation.
The isospin analysis uses as input the branching fractions and
CP-violating charge asymmetries
of all five ρπ decay modes
(ρ+π−,ρ−π+,
ρ0π0, ρ+π0,
ρ0π+).
The relevant information is taken from
HFAG - Rare Decays and is tabulated below.
[Branching fractions are given in units of 10−6.]
Those values that are not included in the table below
can be obtained from the bilinear form-factors,
eg. a measurement
BR(B0 → ρ0π0)/
BR(B0 → ρ+−π−+) = 0.133 ± 0.022 ± 0.023,
is extracted.
With all information in the ρπ channels put together,
Belle
obtain the tighter constraint
68° < φ2 < 95° at 68% confidence level,
for the solution consistent with the Standard Model.
| BR(B0 → ρ+−π−+) = 24.0 ± 2.5 | - |
| BR(B+ → ρ+π0) = 10.8 +1.4−1.5 | ACP(B+ → ρ+π0) = 0.02 ± 0.11 |
| BR(B+ → π+ρ0) = 8.7 +1.0−1.1 | ACP(B+ → π+ρ0) = −0.07 +0.12−0.13 |
NB. It is implied in the above constraints on α ≡ φ2 that a mirror solution at α → α + π ≡ φ2 → φ2 + π also exists.
For more details on the world average for α ≡ φ2, calculated with different statistical treatments, refer to the CKMfitter and UTfit pages.