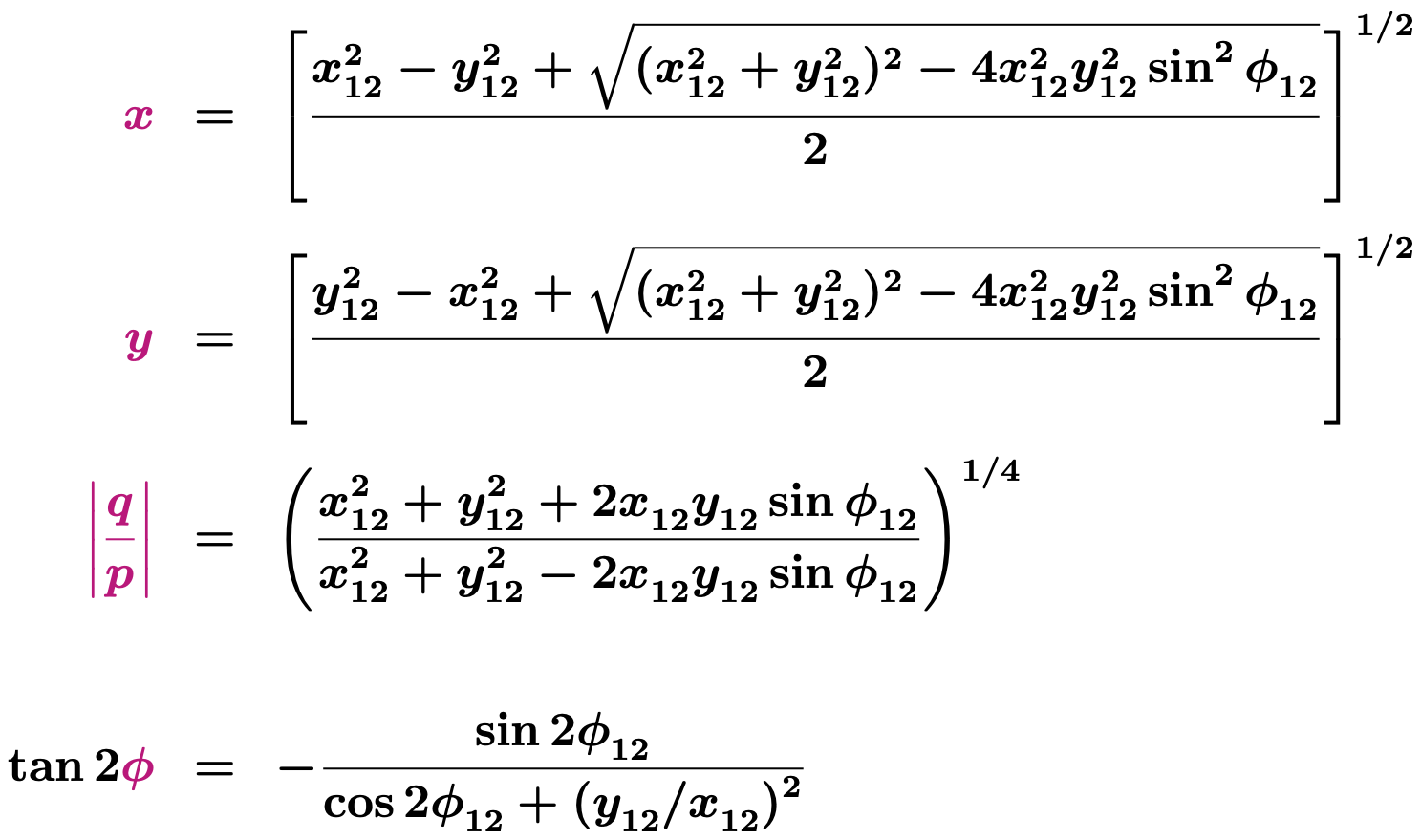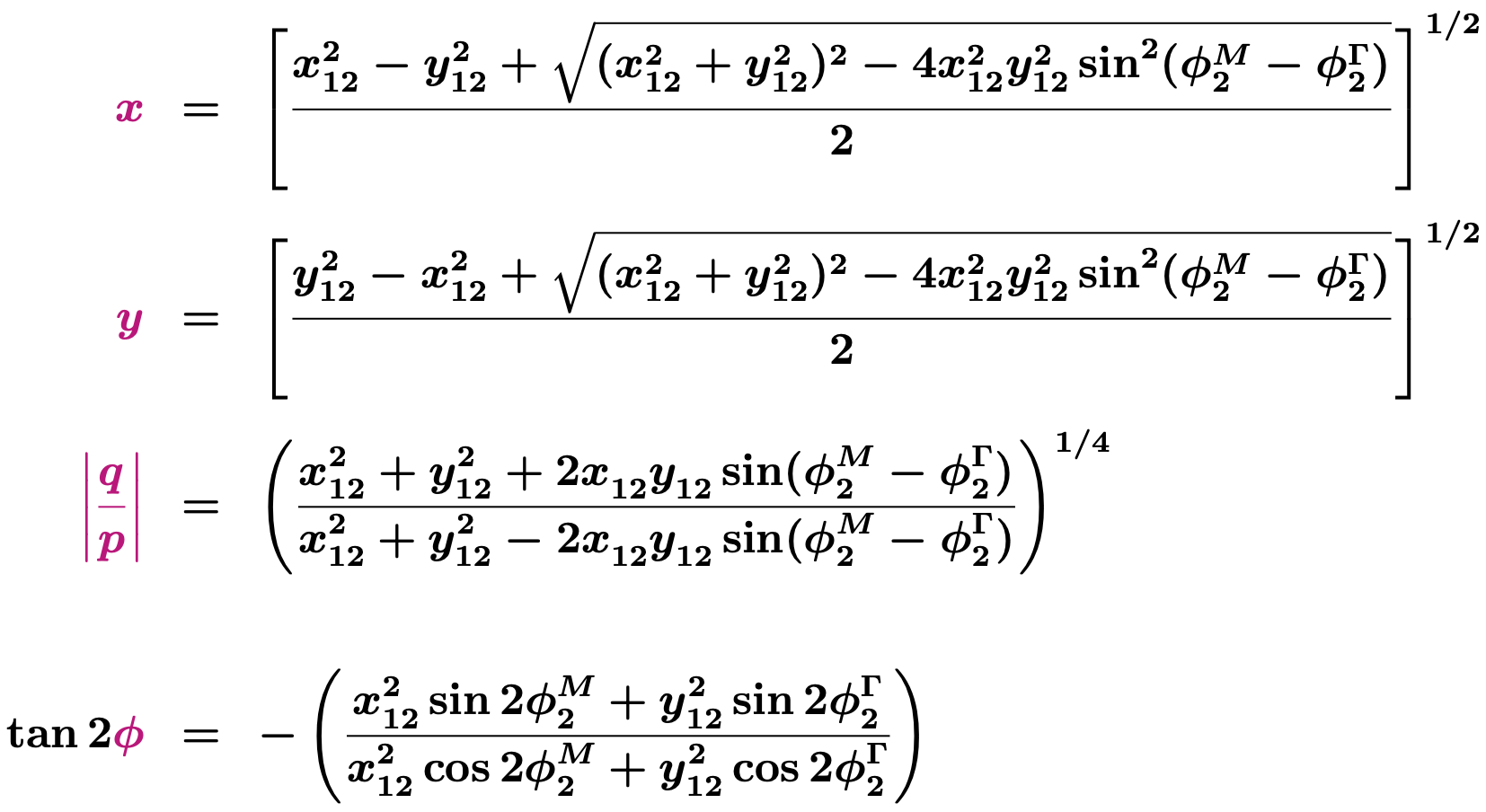Global Fit for D⁰-D⁰ Mixing
(allowing for CP violation)
(through 24 September 2023)

People working on this: Alan Schwartz, Marco Gersabeck
For a complete list of references click here
For world average values of measured observables (used below) click here

Notation:
The mass eigenstates are denoted D₁ ≡ p|D⁰> + q|D⁰> and D₂ ≡ p|D⁰> − q|D⁰>; δ and δ_Kππ are strong phase differences between D⁰ → f and D⁰ → f amplitudes, and φ is the weak phase difference Arg(q/p). We define δ ≡ δ_{D⁰ → K⁻n(π)} − δ_{D⁰
→ K⁻n(π)}. The mixing parameters are defined as x ≡ (m₂ − m₁)/Γ and y ≡ (Γ₂ − Γ₁)/(2Γ), where Γ = (Γ₁ + Γ₂)/2. Our convention is (CP)|D⁰> = −|D⁰> and (CP)|D⁰> = −|D⁰>; thus, in the absence of CP violation, x = (m_CP+ − m_CP−)/Γ and y = (Γ_CP+ − Γ_CP−)/(2Γ).

Experimental Observables:
From all experiments, there are 63 measurements of 18 observables: y_CP, A_Γ, (x, y, |q/p|, φ) _{Belle
K⁰_S π⁺ π ⁻}, (x_CP, y_CP, Δx, Δy) _{LHCb
K⁰_S π⁺ π ⁻}, (x, y) _{BaBar
K⁰_S h⁺ h⁻}, (x, y) _{BaBar
π⁰ π⁺ π⁻}, (R_M)/2 _{LHCb
K⁺ π⁻ π⁺ π ⁻}, (R_M)_semileptonic, (x", y") _{K⁺ π⁻ π ⁰}, (R_D, x², y, cos δ, sin δ) _{CLEOc Ψ(3770)} , (A_CP^Kπ) _{BESIII Ψ(3770)} , (R_D, A_D, x'^2±, y'^±)_BaBar, (R_D, A_D, x'^2±, y'^±)_Belle, (R_D, x'², y') _CDF, (R_D^±, x'^2±, y'^±) _LHCb, (A_CP^K, A_CP^π) _BaBar, (A_CP^K, A_CP^π) _Belle, (A_CP^K − A_CP^π) _CDF, (A_CP^K −A_CP^π) _LHCb(D^*), (A_CP^K −A_CP^π) _{LHCb(B →D⁰μX)}, (A_CP^K) _LHCb(D^*)

Theoretical Parameters:
Allowing for all CP violation, there are 10 fitted parameters: x, y, δ, δ_Kππ, R_D, A_D, A_π, A_K, |q/p|, and Arg(q/p) = φ. The first two parameters govern mixing; the next two are strong phases; R_D is the ratio Γ(D⁰→ f)/Γ(D⁰ → f); the next three are direct CP-violating asymmetries for D⁰ → K⁺ π⁻, D⁰ → π⁺ π⁻, and D⁰ → K⁺ K⁻, respectively; and the last two are indirect CP-violating parameters. The phase φ corresponds to a basis in which the dominant U-spin-changing (ΔU=2) dispersive and absorptive mixing amplitudes are real; see Kagan and Silvestrini, Eq. 107. (Choosing a basis ensures that Arg(q/p) is physically meaningful.) The relationships between these parameters and the measured observables are given below. The observables appear in blue (on the left sides of the equations), the underlying parameters in magenta (on the right sides), and intermediate variables in black.

In addition, we perform a fit for alternative mixing and CP violation parameters as described below: (x₁₂, y₁₂, φ₁₂) for Fit #2, and (x₁₂, y₁₂, φ^M₂, φ^Γ₂) for Fit #3.

Measurements used:

Index Observable Value Source

1 y_CP − y_CP(Kπ) (0.697 ± 0.028)%

World average of D⁰ → K⁺ K⁻ / π⁺ π ⁻ / K⁺ K⁻ K⁰

Our calculation of the y_CP(Kπ) correction is from arXiv:2207.11867, Eq. (29).

This correction was first pointed out by Pajero, Morello in JHEP 03 (2022) 162.

2 A_Γ (0.0089 ± 0.0113)% World average (COMBOS combination) of D⁰ → K⁺ K⁻ / π⁺ π ⁻ results

3-6

x (no CPV)

y (no CPV)

|q/p| (no dCPV)

Arg(q/p)=φ (no dCPV)

x

y

|q/p|

φ

0.56 ± 0.19 ^+0.067 _−0.127

0.30 ± 0.15 ^+0.050 _−0.078

0.90 ^+0.16 _−0.15 ^+0.078 _−0.064

(−6 ± 11 ^+4.2 ₋₅) degrees

(0.58 ± 0.19 ^+0.0734 _−0.1177)%

(0.27 ± 0.16 ^+0.0546 _−0.0854)%

0.82 ^+0.20 _−0.18 ^+0.0807 _−0.0645

(−13 ⁺¹² ₋₁₃ ^+4.15 _−4.77) degrees

Belle D⁰ → K⁰ _S π⁺ π ⁻ results using 921 fb⁻¹.

Correlation coefficient is +0.012 for no-CPV; for CPV-allowed they are:

1 0.054 −0.074 −0.031

0.054 1 0.034 −0.019

−0.074 0.034 1 0.044

−0.031 −0.019 0.044 1

7-10

11-14

x (no CPV)

y (no CPV)

x_CP

y_CP

Δx

Δy

x_CP

y_CP

Δx

Δy

(−0.86 ± 0.53 ± 0.17)%

(0.03 ± 0.46 ± 0.13)%

(0.27 ± 0.16 ± 0.04)%

(0.74 ± 0.36 ± 0.11)%

(−0.053 ± 0.070 ± 0.022)%

(0.06 ± 0.16 ± 0.03)%

(0.400 ± 0.045 ± 0.020)%

(0.551 ± 0.116 ± 0.059)%

(−0.029 ± 0.018 ± 0.001)%

(0.031 ± 0.035 ± 0.013)%

LHCb D⁰ → K⁰_S π⁺π⁻ results using 1 fb^-1 (√s = 7 TeV)

D^*+ → D⁰π⁺ flavor tag. Correlation coefficient = +0.37, no CPV.

3 fb^-1 results (√s = 7, 8 TeV) allowing for CPV.

D^*+ → D⁰π⁺, B → D⁰μ⁻ X flavor tags. Correlation coefficients (stat. + syst.):

1 (−0.17 + 0.15) (0.04 + 0.01) (−0.02 − 0.02)

1 (−0.03 − 0.05) (0.01 − 0.03)

1 (−0.13 + 0.14)

5.4 fb^-1 results (√s = 13 TeV) allowing for CPV.

D^*+ → D⁰π⁺, B → D⁰μ⁻ X flavor tags. Correlation coefficients (stat. + syst.):

1 (0.121 + 0.13) (−0.018 + 0.01) (−0.016 + 0.01)

1 (−0.012 − 0.02) (−0.058 + 0.01)

1 (0.069 + 0.31)

For (x, y, |q/p|, φ) → (x_CP, y_CP, Δx, Δy) mapping, see PRD 99, 012007 (2019)

15-16

x

y

(0.16 ± 0.23 ± 0.12 ± 0.08)%

(0.57 ± 0.20 ± 0.13 ± 0.07)%

BaBar D⁰ → K⁰_S π⁺π⁻ and D⁰ → K⁰_S K⁺ K⁻ combined;

Correlation coefficient = +0.0615, no CPV.

17-18

x

y

(1.5 ± 1.2 ± 0.6)%

(0.2 ± 0.9 ± 0.5)%

BaBar D⁰ → π⁰ π⁺π⁻

Correlation coefficient = −0.006, no CPV.

19 (x² + y²)/2 (0.0130 ± 0.0269)% World average (COMBOS combination) of D⁰ → K⁺l⁻ ν results

20-21

x"

y"

(2.61 ^+0.57 _−0.68 ± 0.39)%

(−0.06 ^+0.55 _−0.64 ± 0.34)%

BaBar K⁺ π ⁻ π ⁰ result; correlation coefficient = −0.75.

Note: x" = x cos δ_Kππ + y sin δ_Kππ, y" = y cos δ_Kππ − x sin δ_Kππ.

22-26

R_D

x²

y

cos δ

sin δ

(0.533 ± 0.107 ± 0.045)%

(0.06 ± 0.23 ± 0.11)%

(4.2 ± 2.0 ± 1.0)%

0.81 ^+0.22_−0.18 ^+0.07_−0.05

−0.01 ± 0.41 ± 0.04

CLEO-c Ψ(3770) results, 0.82 fb⁻¹. Correlation coefficients:

1 0 0 −0.42 0.01

1 −0.73 0.39 0.02

1 −0.53 −0.03

1 0.04

1

27-29

R_D

x'²⁺

y'⁺

(0.303 ± 0.0189)%

(−0.024 ± 0.052)%

(0.98 ± 0.78)%

BaBar K⁺ π ⁻ results; correlation coefficients:

1 +0.77 −0.87

+0.77 1 −0.94

−0.87 −0.94 1

30-32

A _D

x'^{2 −}

y'⁻

(−2.1 ± 5.4)%

(−0.020 ± 0.050)%

(0.96 ± 0.75)%

BaBar K⁺ π ⁻ results; correlation coefficients same as above.

33-35

(no CPV)

R_D

x'²

y'

(0.353 ± 0.013)%

(0.009 ± 0.022)%

(0.46 ± 0.34)%

Belle K⁺ π ⁻ no-CPV results using 976 fb⁻¹. Correlation coefficients:

1 +0.737 −0.865

+0.737 1 −0.948

−0.865 −0.948 1

33-35

R_D

x'²⁺

y'⁺

(0.364 ± 0.018)%

(0.032 ± 0.037)%

(−0.12 ± 0.58)%

Belle K⁺ π ⁻ CPV-allowed results using 400 fb⁻¹. Correlation coefficients:

1 +0.655 −0.834

+0.655 1 −0.909

−0.834 −0.909 1

36-38

A _D

x'^{2 −}

y'⁻

(2.3 ± 4.7)%

(0.006 ± 0.034)%

(0.20 ± 0.54)%

Belle K⁺ π ⁻ CPV-allowed results using 400 fb⁻¹;

correlation coefficients same as above.

39-41

R_D

x'²

y'

(0.351 ± 0.035)%

(0.008 ± 0.018)%

(0.43 ± 0.43)%

CDF K⁺ π ⁻ results for 9.6 fb⁻¹. Correlation coefficients:

1 0.90 −0.97

0.90 1 −0.98

−0.97 −0.98 1

42-44

R_D⁺

x'²⁺

y'⁺

(0.338 ± 0.0161)%

(−0.0019 ± 0.0447)%

(0.581 ± 0.526)%

LHCb K⁺ π ⁻ results for 3.0 fb⁻¹ (√s = 7, 8 TeV)
B → D^*+μ⁻ X, D^*+ → D⁰π⁺ flavor tags. Correlation coefficients:

1 0.823 −0.920

0.823 1 −0.962

−0.920 −0.962 1

45-47

R_D⁻

x'^{2 −}

y'⁻

(0.360 ± 0.0166)%

(0.0079 ± 0.0433)%

(0.332 ± 0.523)%

LHCb K⁺ π ⁻ results for 3.0 fb⁻¹ (√s = 7, 8 TeV)
B → D^*+μ⁻ X, D^*+ → D⁰π⁺ flavor tags. Correlation coefficients:

1 0.812 −0.918

0.812 1 −0.956

−0.918 −0.956 1

48-50

R_D⁺

x'²⁺

y'⁺

(0.3454 ± 0.0045)%

(0.0061 ± 0.0037)%

(0.501 ± 0.074)%

LHCb K⁺ π ⁻ results for 5.0 fb⁻¹ (√s = 7, 8 TeV)
D^*+ → D⁰π⁺ flavor tag. Correlation coefficients:

1 0.843 −0.935

0.843 1 −0.963

−0.935 −0.963 1

51-53

R_D⁻

x'^{2 −}

y'⁻

(0.3454 ± 0.0045)%

(0.0016 ± 0.0039)%

(0.554 ± 0.074)%

LHCb K⁺ π ⁻ results for 5.0 fb⁻¹ (√s = 7, 8 TeV)
D^*+ → D⁰π⁺ flavor tag. Correlation coefficients:

1 0.846 −0.935

0.846 1 −0.964

−0.935 −0.964 1

54-55

A_CP^K

A_CP^π

(0.00 ± 0.34 ± 0.13)%

(−0.24 ± 0.52 ± 0.22)%

BaBar 385.8 fb⁻¹ near ϒ(4S) resonance

56-57

A_CP^K

A_CP^π

(−0.43 ± 0.30 ± 0.11)%

(0.43 ± 0.52 ± 0.12)%

Belle 540 fb⁻¹ near ϒ(4S) resonance

58-59

A_CP^K

A_CP^π

(−0.32 ± 0.21)%

(0.31 ± 0.22)%

CDF 9.7 fb⁻¹ pp collisions at √s = 1.96 TeV

( 〈t〉_K − 〈t〉_π ) / τ_D = 0.27 ± 0.01

60 A_CP^K − A_CP^π (−0.154 ± 0.029)%

LHCb 8.9 fb⁻¹ pp collisions at √s = 7, 8, 13 TeV

D^*+ → D⁰π⁺ and B → D⁰μ⁻ X flavor tags

( 〈t〉_K − 〈t〉_π )/τ_D = 0.115 ± 0.002; 〈t〉/τ_D = 1.71 ± 0.10

61 A_CP^K (0.068 ± 0.054 ± 0.016)%

LHCb 5.7 fb⁻¹ pp collisions at √s = 13 TeV

D^*+ → D⁰π⁺ flavor tags

〈t〉_K /τ_D = (701.5 ± 1.1)/(410.3 ± 1.0) = 1.7097 ± 0.0050

62 (x² + y²)/4 (0.0048 ± 0.0018)%

LHCb 3.0 fb⁻¹ pp collisions at √s = 7, 8 TeV

D⁰ → K⁺ π ⁻ π ⁺ π ⁻

63 A_CP^Kπ 0.132 ± 0.011 ± 0.007

BESIII Ψ(3770) results, 2.93 fb⁻¹. D⁰ → K⁻ π⁺,

difference between CP-even tagged and CP-odd tagged

MINUIT fit results
Four types of fits are performed, as follows:

Fit #1: no CP violation (A_D= 0, A_K= 0, A_π= 0, |q/p| = 1, φ = 0)

Fit #2: One-parameter description of indirect CP violation
This parametrization results from two simplifications: (1) sub-leading amplitudes in CF and DCS decays are neglected; and (2) sub-leading amplitudes in SCS decays are neglected in indirect CP violation observables, as their contribution is suppressed by mixing parameters x and y. These simplifictions have two consequences: (a) no direct CP violation in CF or DCS decays (A_D= 0); and (b) only short-distance dispersive amplitudes contribute to indirect CP violation. Thus Arg(Γ₁₂) = 0 (in the ΔU=2 basis, see note on Arg(q/p) above), and all indirect CP violation can be parameterized in terms of a phase difference between M₁₂ and Γ₁₂. This phase difference is denoted φ₁₂ ≡ Arg(M₁₂/Γ₁₂). The magnitudes of the mixing amplitudes are parameterized as x₁₂ ≡ 2|M₁₂|/Γ and y₁₂ ≡ |Γ₁₂|/Γ. The "baseline" mixing + CPV parameters (x, y, |q/p|, φ) can be expressed in terms of (x₁₂, y₁₂, φ₁₂); since four parameters depend only on three, there must be an additional constraint among the four. This relation, first derived by Ciuchini et al. and later independently obtained by Kagan and Sokoloff, is tanφ = (1-|q/p|²)/(1+|q/p|²) × (x/y). Alternatively, one can use the quadratic equation (15) of Grossman, Nir, and Perez to reduce four parameters to three (e.g., see here).

We thus perform three separate fits:
2a: float x, y, and φ, and use the Ciuchini/Kagan formula to derive |q/p|; this yields proper (MINOS) errors for φ.
2b: float x, y, and |q/p|, and use the Ciuchini/Kagan formula to derive φ; this yields proper (MINOS) errors for |q/p|.
2c: fit for parameters x₁₂, y₁₂, and φ₁₂. The relationships between these parameters and (x, y, |q/p|, φ) are derived by Kagan and Sokoloff (Eqs. 14, 15, 48, 52), but a factor of 1/√2 is missing from Eqs. (14) and (15):

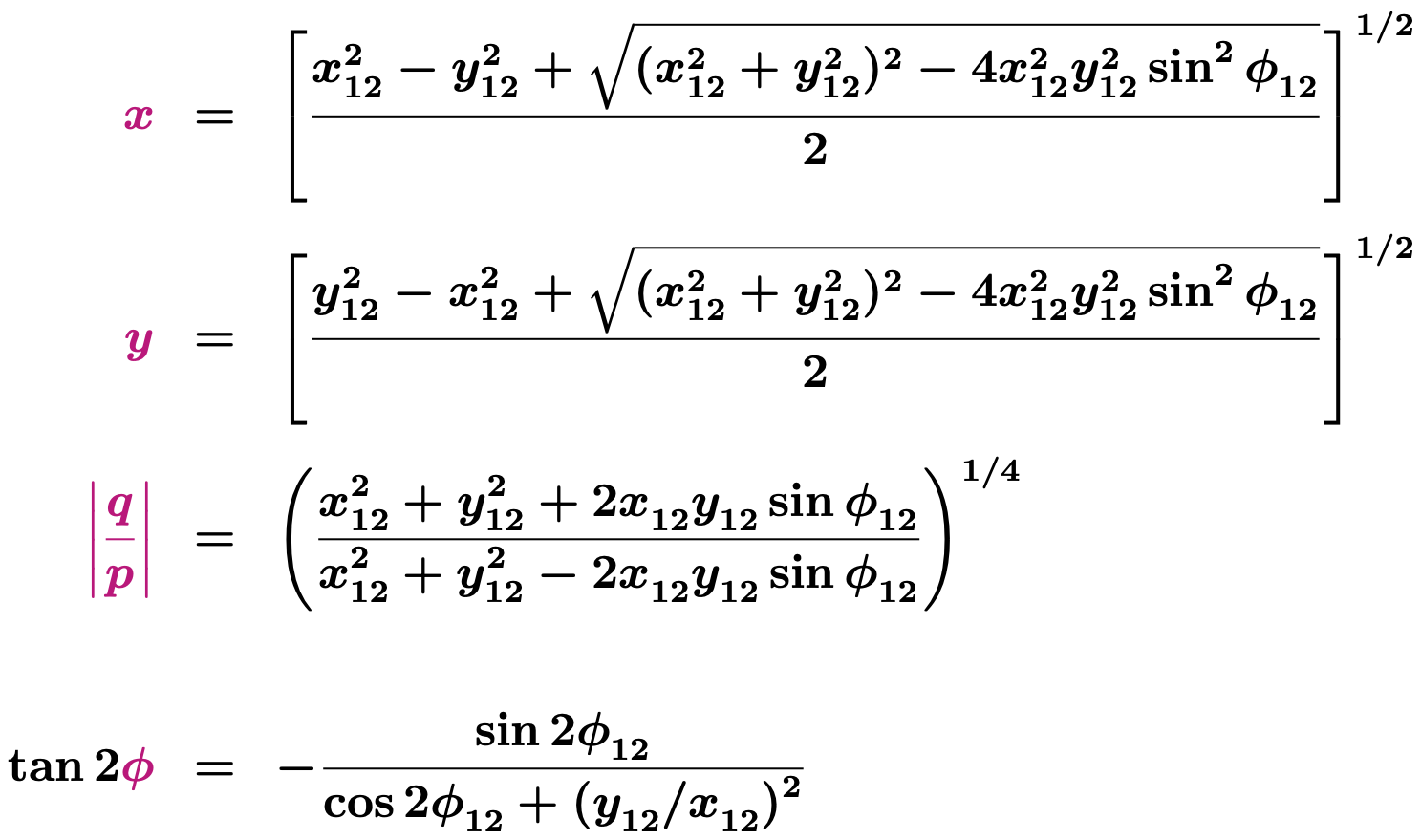
Fit #3: Two-parameter description of indirect CP violation
In this parameterization, sub-leading amplitudes in CF and DCS decays are neglected as in Fit #2, and thus A_D= 0. However, to accommodate the "high-precision era" in charm mixing/CP violation measurements, sub-leading amplitudes in SCS decays are taken into account in indirect CP violation observables. There is one simplification: D⁰→ K⁺K⁻, π⁺π⁻ final-state-dependent effects are neglected in A_Γ, as they cancel at leading-order in U-spin breaking. The sub-leading SCS amplitudes contribute to Γ₁₂ in addition to M₁₂, and thus Arg(Γ₁₂) may be nonzero. To account for this, we fit for four parameters: (x₁₂, y₁₂, φ^M₂, φ^Γ₂), where φ^M₂ and φ^Γ₂ are the phases of M₁₂ and Γ₁₂, respectively, relative to that of the dominant ΔU=2 dispersive and absorptive amplitudes. This parameterization is discussed in Kagan and Silvestrini. The relationships between (x, y, |q/p|, φ) and (x₁₂, y₁₂, φ^M₂, φ^Γ₂) are:

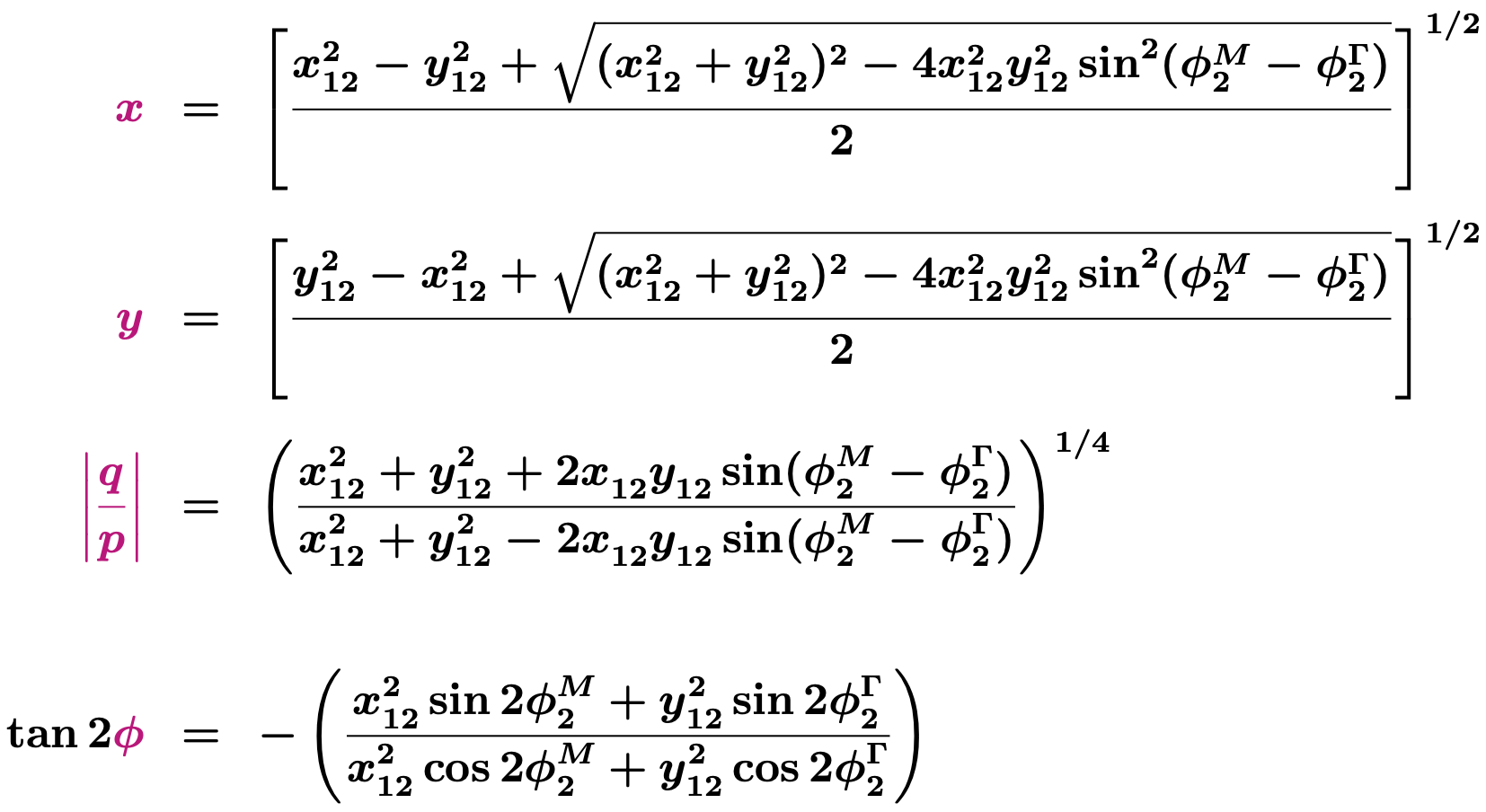
The first three relations correspond to Eqs. (14), (15), and (48) of Kagan and Sokoloff; the last relation corresponds to Eq. (110) of Kagan and Silvestrini.

Fit #4: Two-parameter description of indirect CP violation (|q/p|, φ), direct CP violation in DCS decays allowed
In this case all parameters are floated, and we fit for the baseline parameters (x, y, |q/p|, φ).

The MINUIT output for Fits #1 − #4 are given here.
Note that x, y, R _D, A _D, A _π and A _K are in percent; δ, δ₂ (= δ_Kππ), and φ are in radians. Correlation coefficients among parameters are listed at the end.

The final results are:

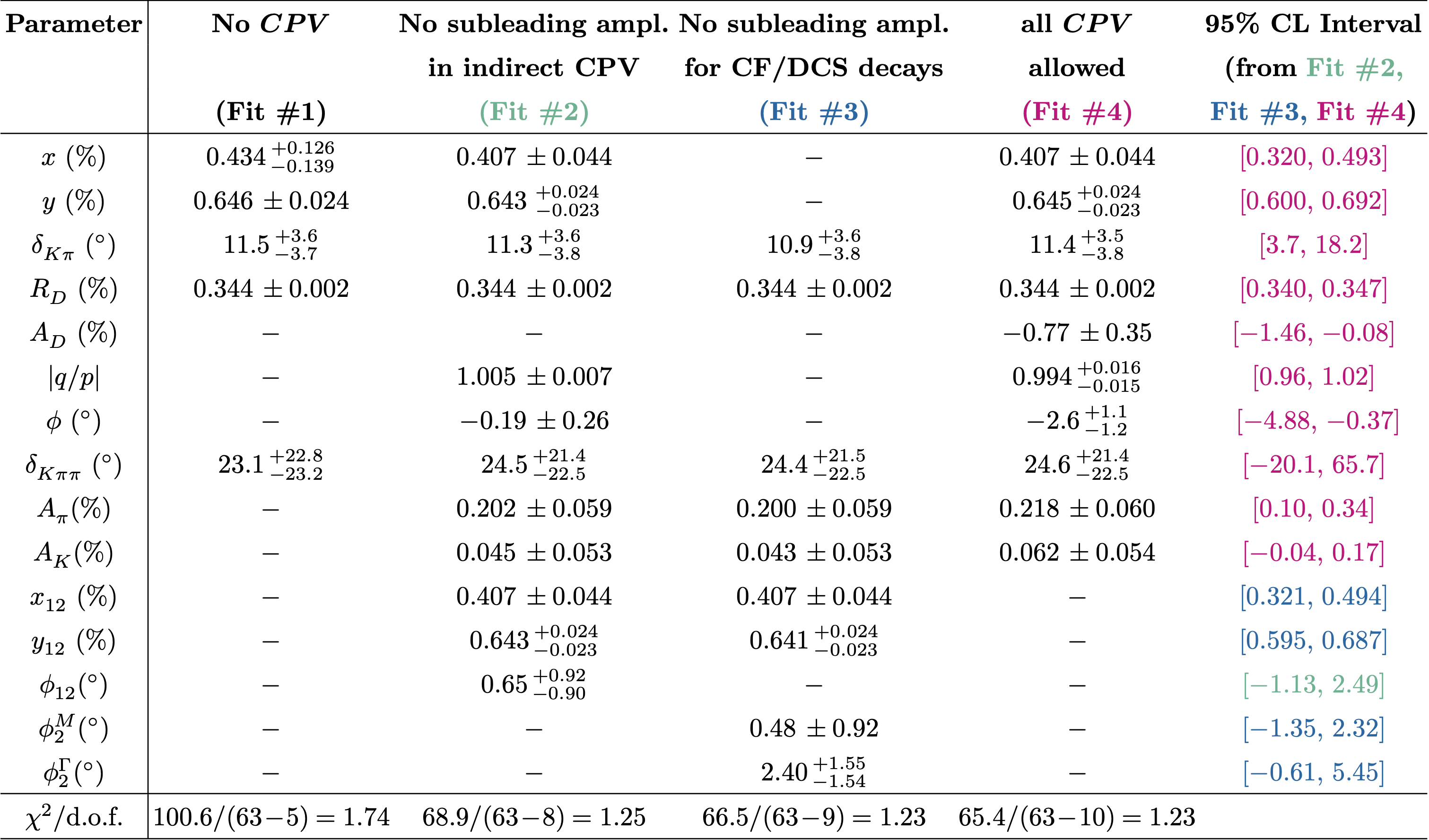
χ ² contributions for the all-CPV-allowed fit #4:

_____________________________________________

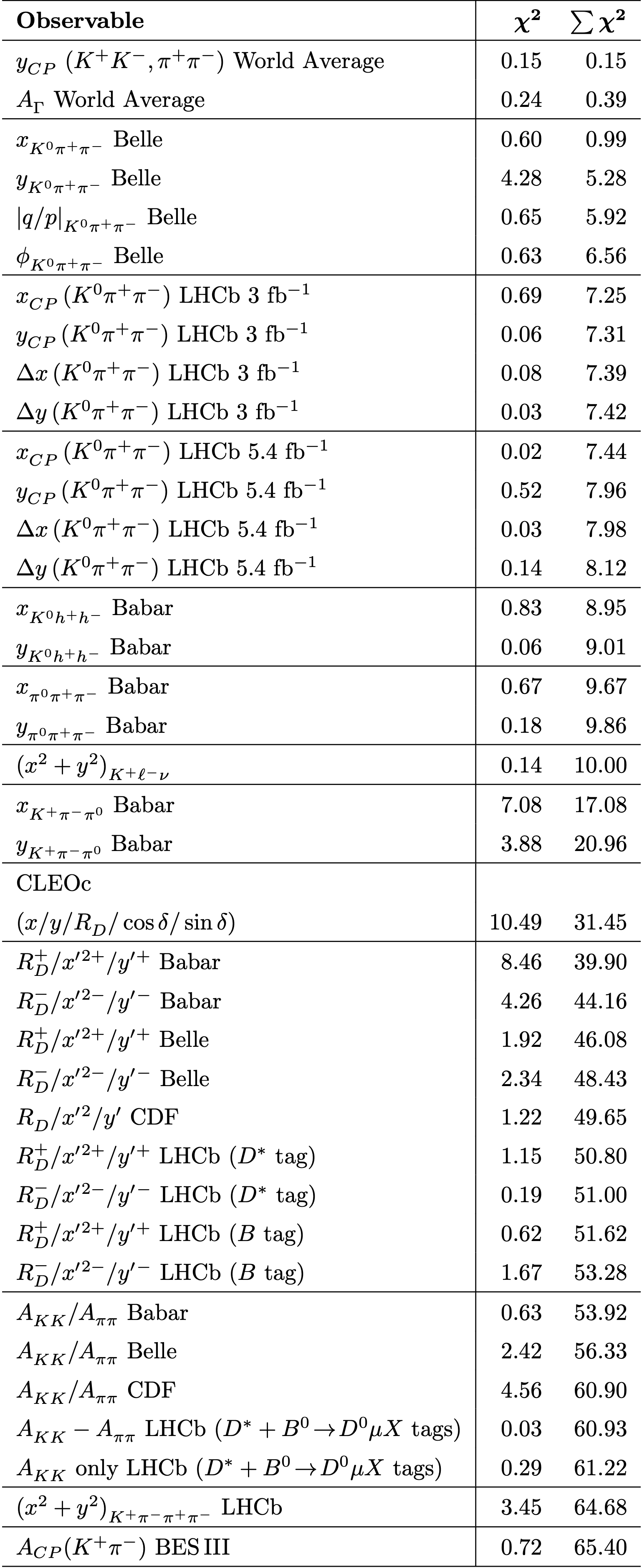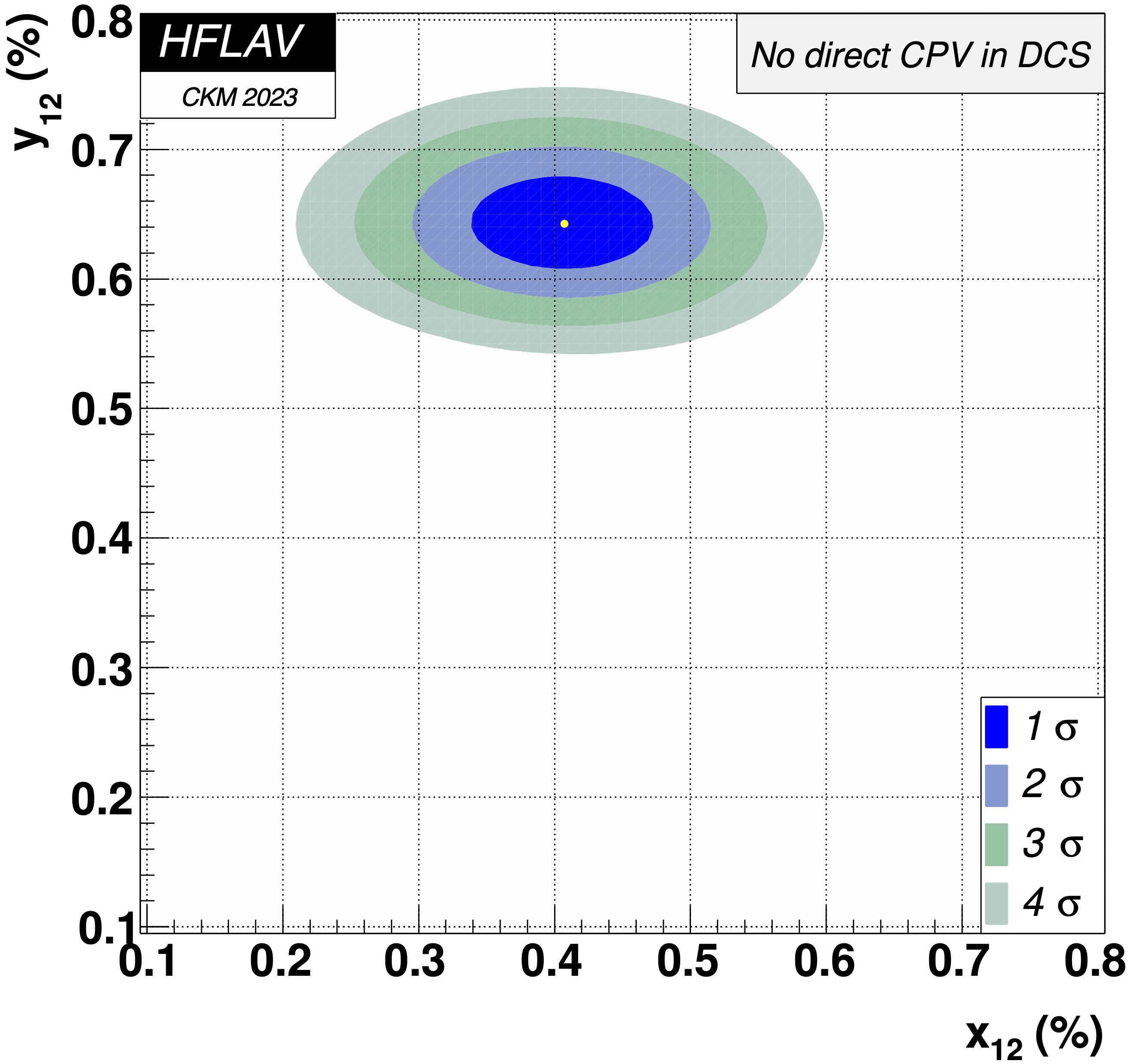
MNCONTOUR-like 2-d plots:
(click on for .pdf versions)

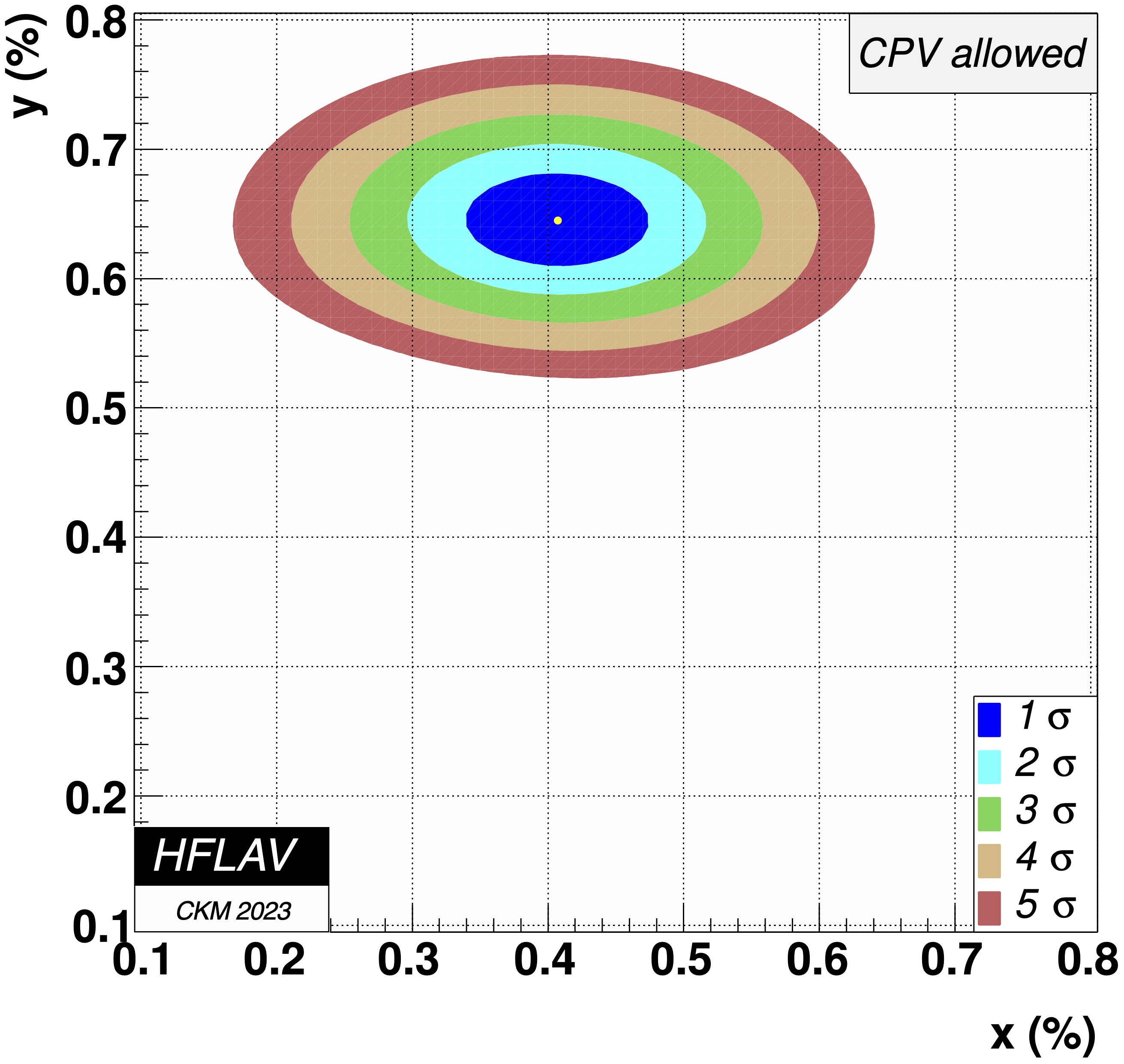
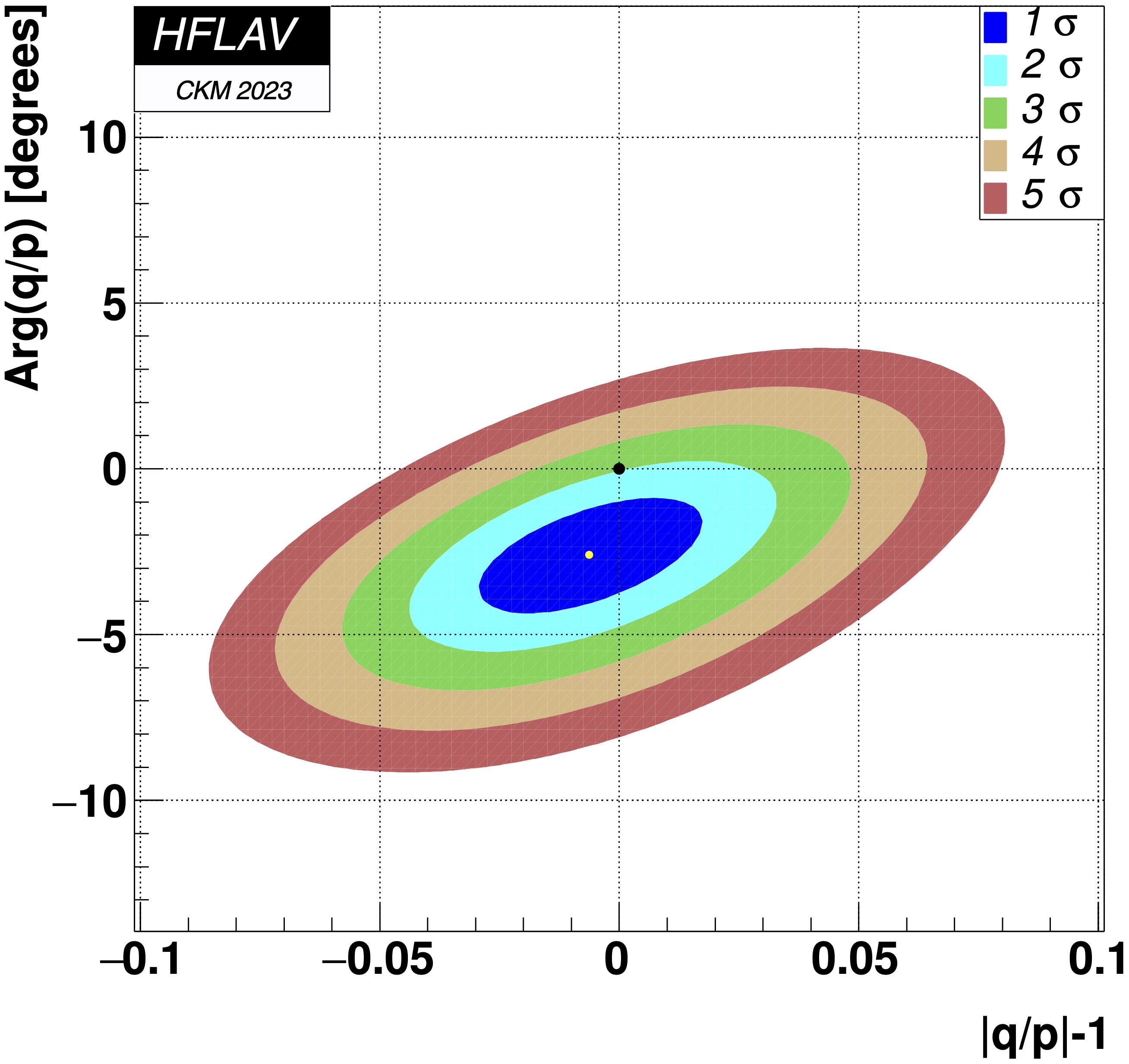
CPV-allowed plot, no mixing (x,y) = (0,0) point: Δχ² = 2631, excluded at ≫ 11.5σ (limit of CERNLIB PROB routine)

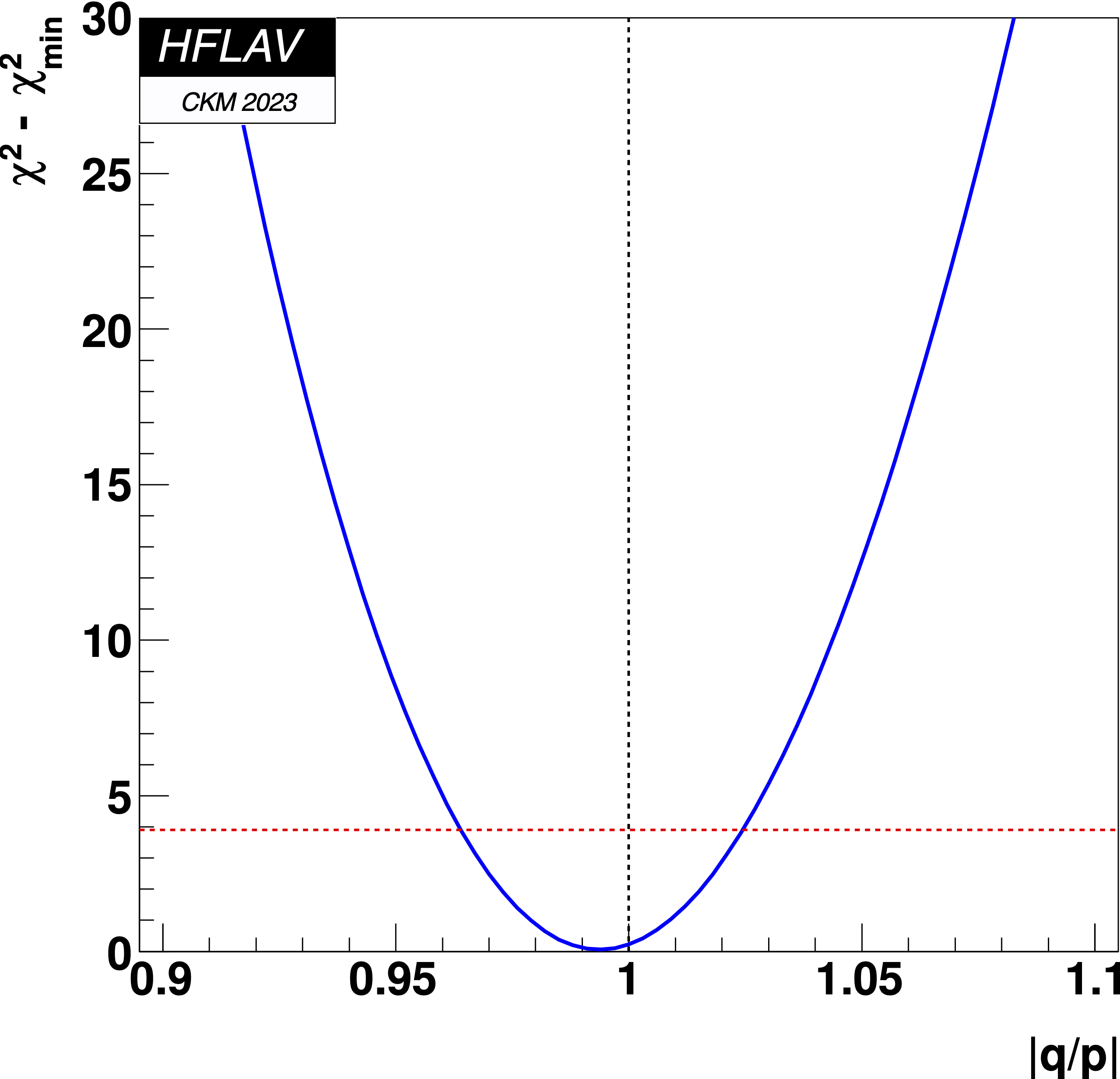
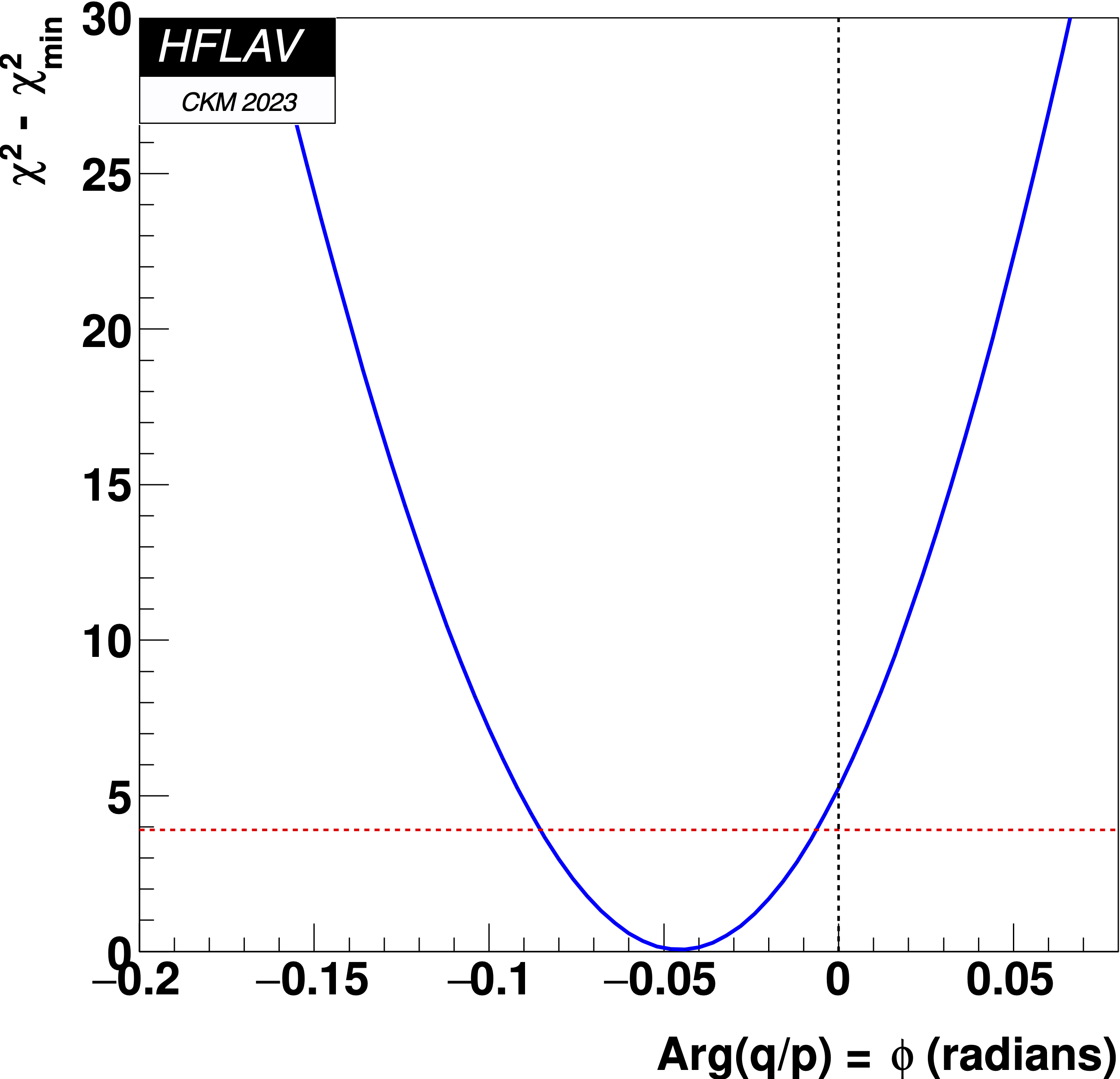
No CPV (|q/p|, φ) = (1,0) point: Δχ² = 6.487, excluded at 2.1σ

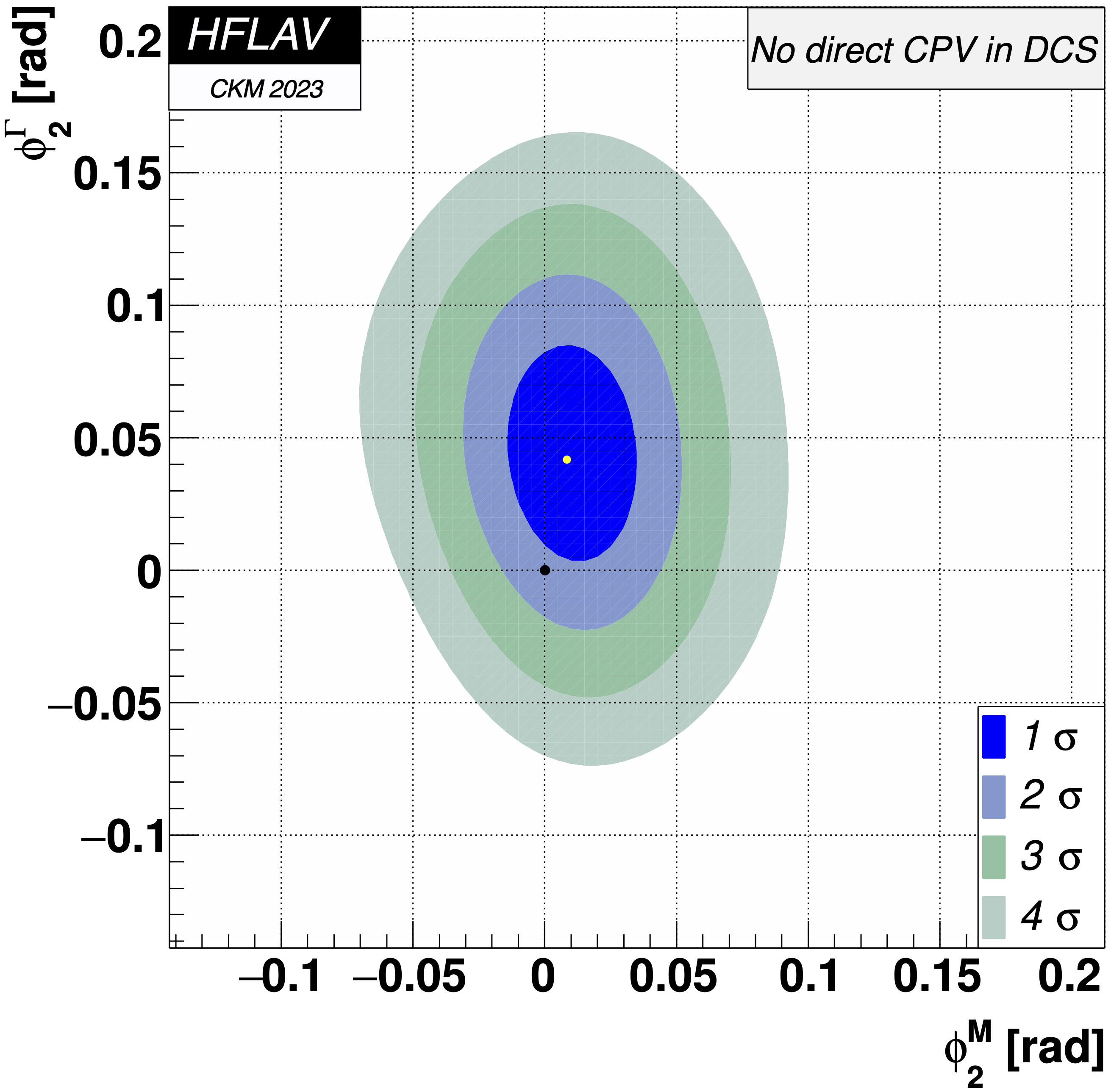
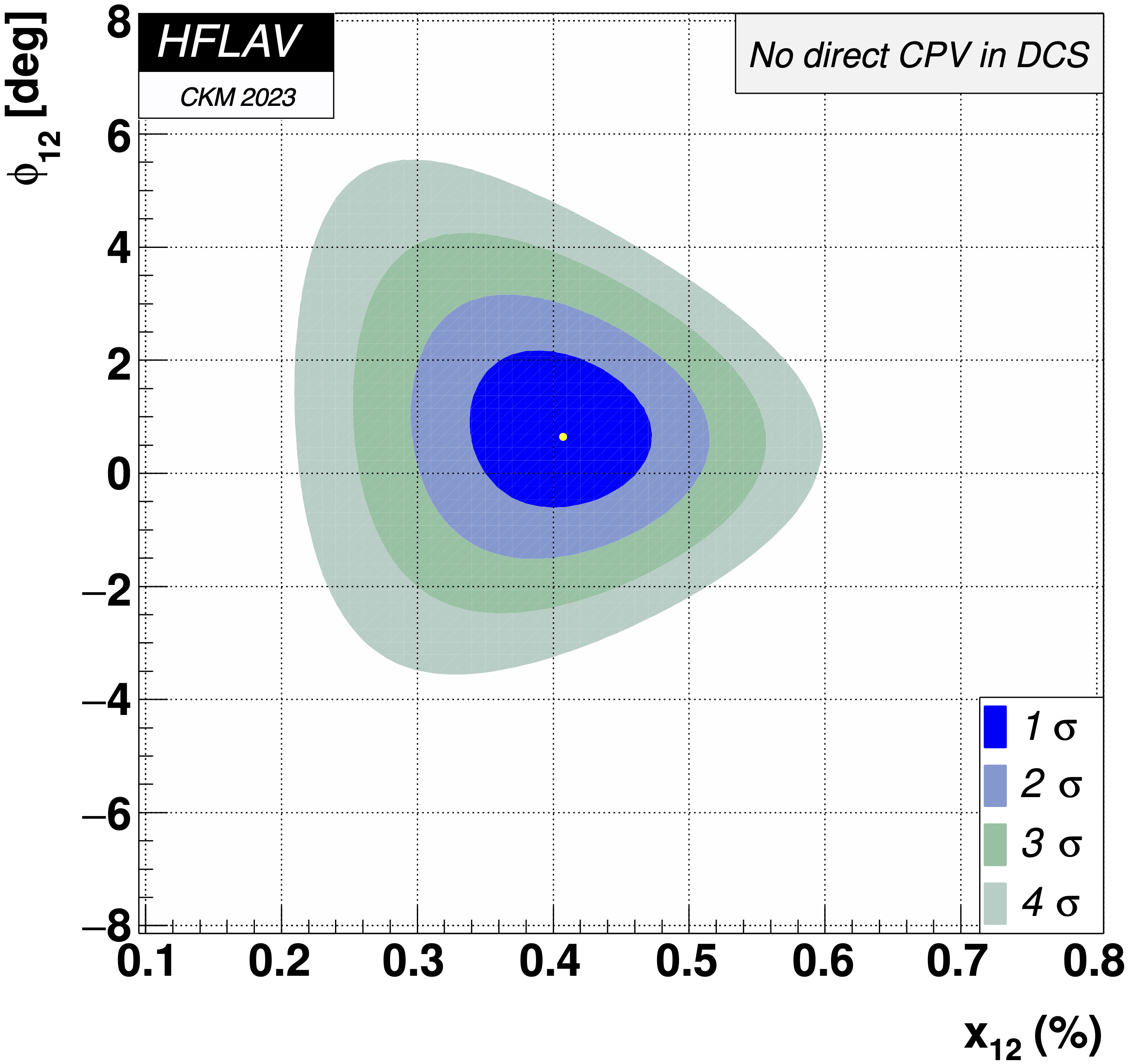
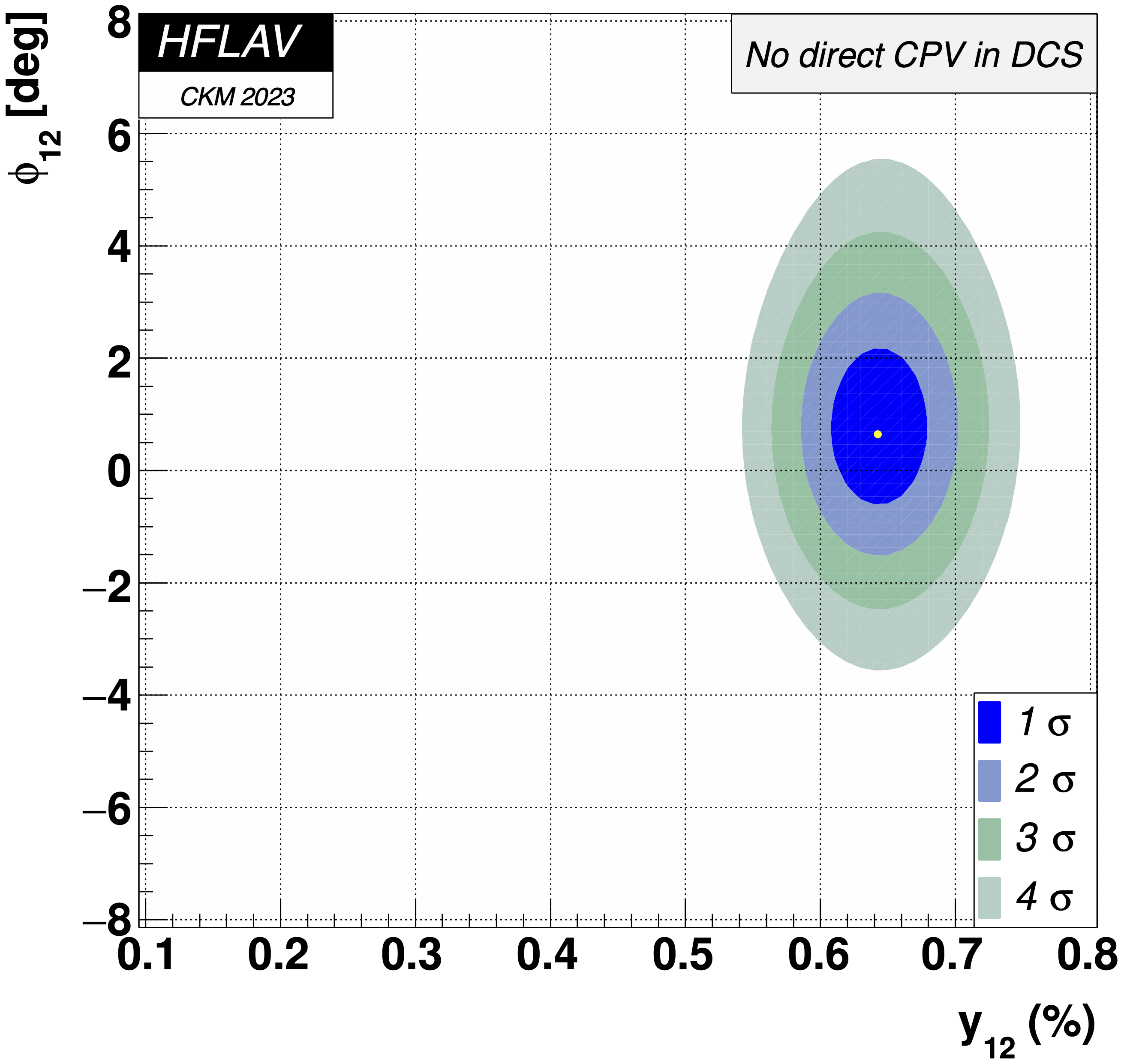
No CPV (φ₂^M, φ₂^Γ) = (0,0) point: Δχ² = 3.399, excluded at 1.3σ
(Note: compared to the (|q/p|, φ) fit, the constraint A_D = 0 raises the χ² of the best-fit point, lowering Δχ² of the no-CPV point)

_____________________________________________

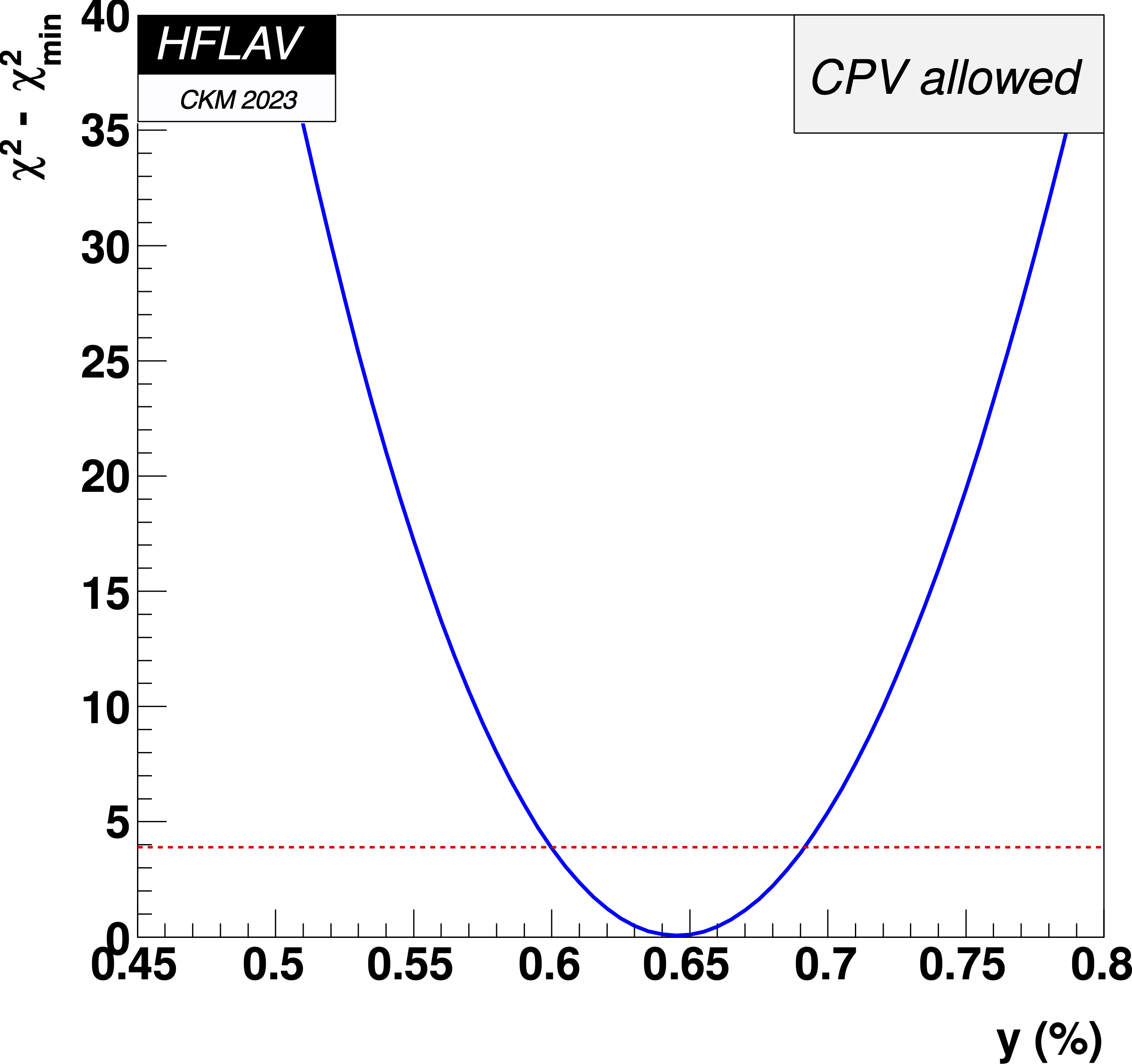
MNCONTOUR-like 1-d plots:
Dashed red horizontal line denotes Δχ² = 3.84, corresponding to a 95% C.L. interval.
(click on for .pdf versions)

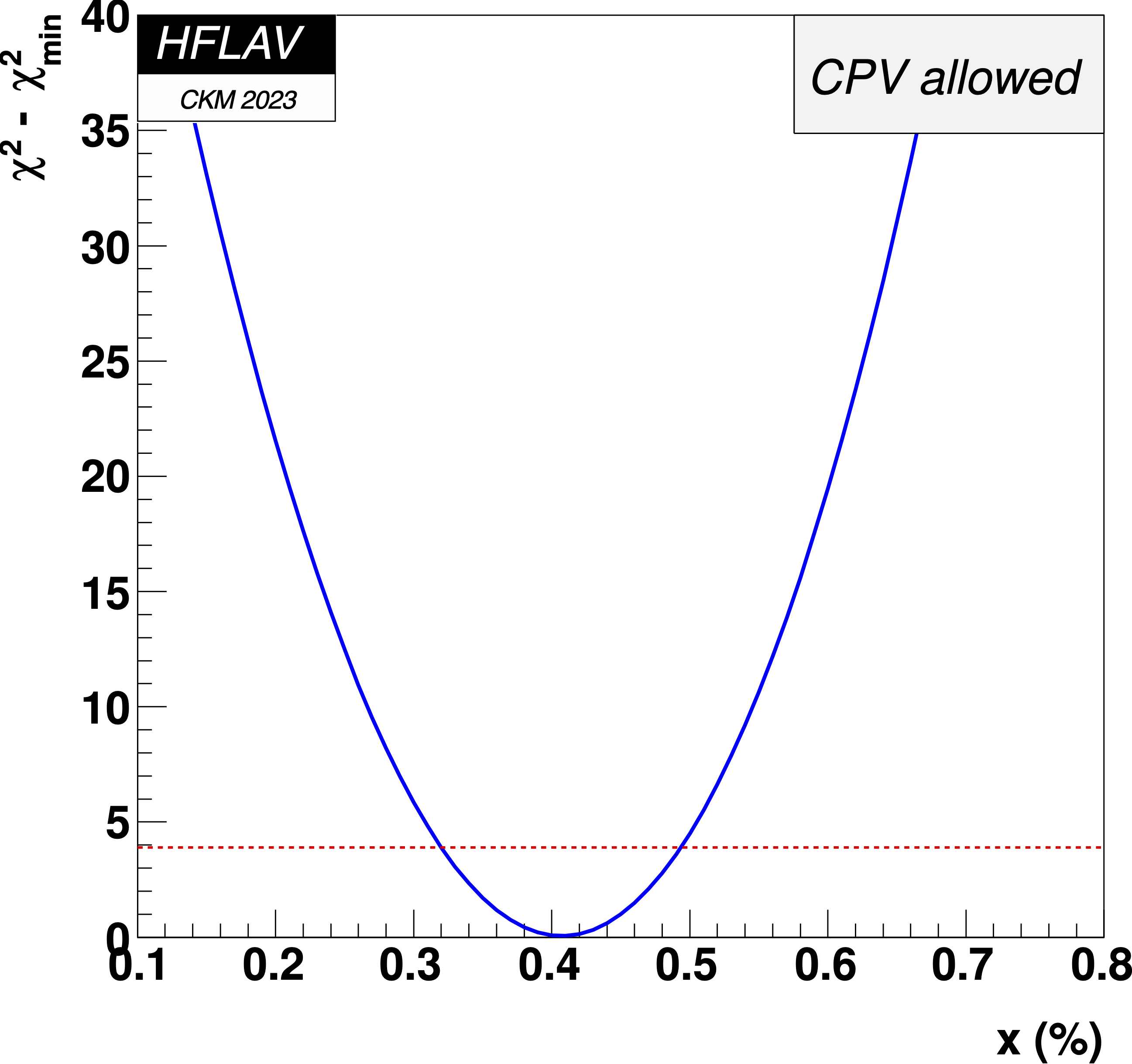
x = 0 point: Δχ² = 82.83, x ≤ 0 excluded at 9.1σ y = 0 point: Δχ² = 1227, y ≤ 0 excluded at > 11.5σ (limit of CERNLIB PROB)

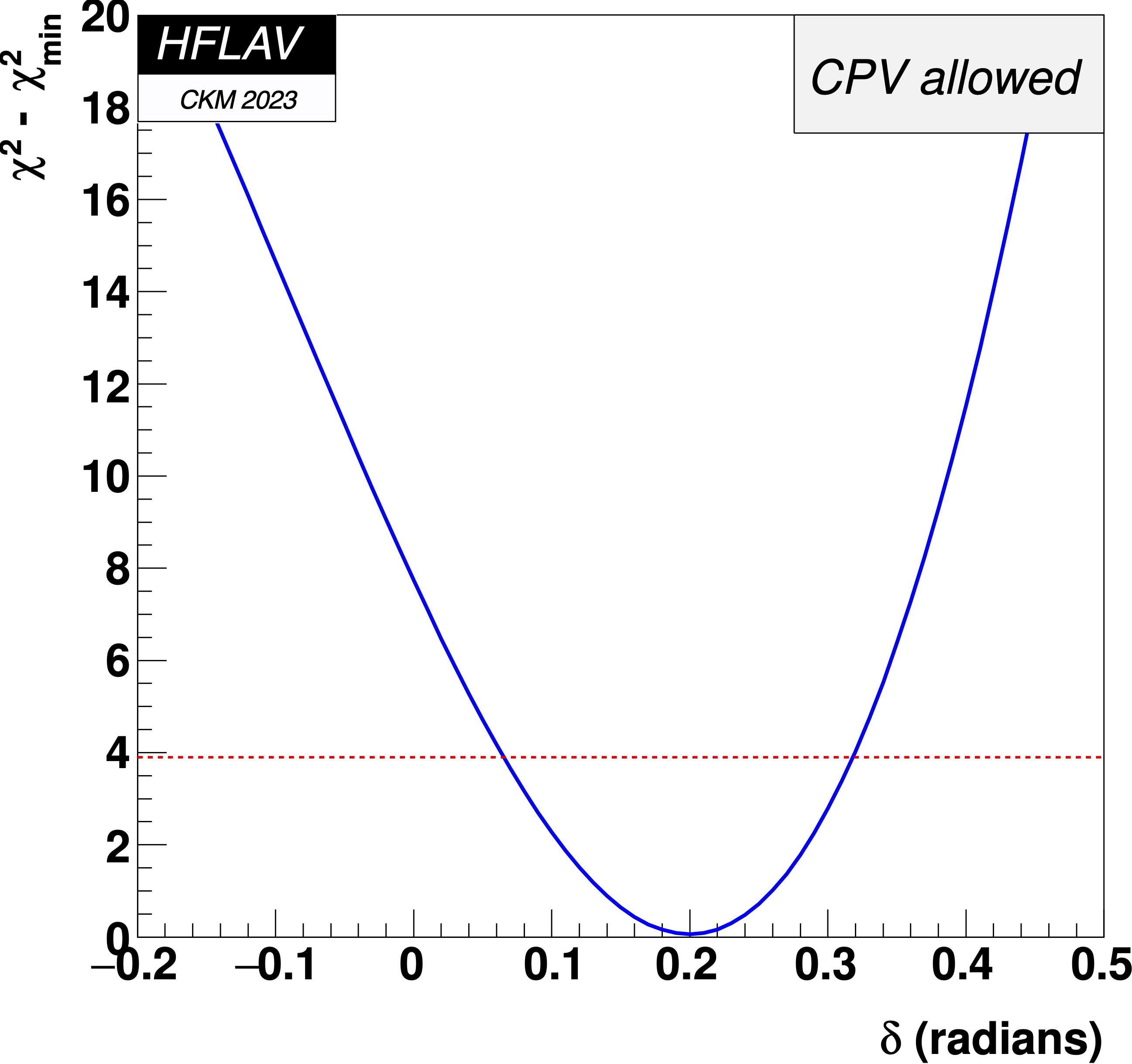
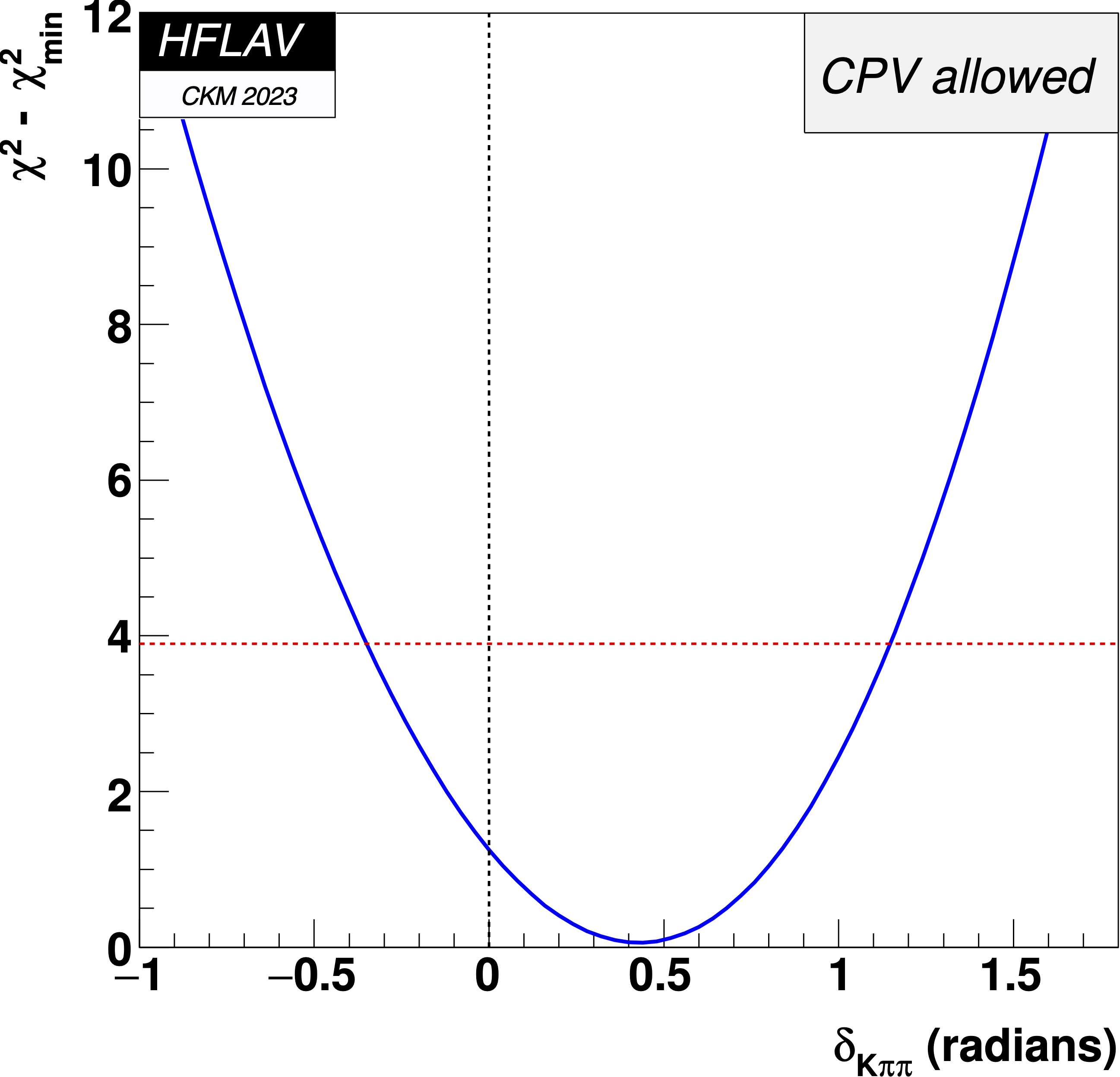
This page is maintained by A. Schwartz and was last updated

Global Fit for D0-D0 Mixing (allowing for CP violation) (through 24 September 2023)

Global Fit for D⁰-D⁰ Mixing
(allowing for CP violation)
(through 24 September 2023)