 Time-dependent CP violation & Unitarity Triangle angles
Time-dependent CP violation & Unitarity Triangle angles
 Time-dependent CP violation & Unitarity Triangle angles
Time-dependent CP violation & Unitarity Triangle angles
|
Overview
Summary plots and values for the latest world averages of the CKM Unitarity Triangle Angles.|
|
|
|
|
eps.gz png |
pdf png |
pdf png |
pdf png |
Measurements related to the CKM angle β ≡ φ1:
| § Studies of b → ccs Transitions |
| § Studies of Colour Suppressed b → cud Transitions |
| § Studies of b → ccd Transitions |
§
Studies of b → qqs (penguin) Transitions
|
| § Studies of b → qqd (penguin) Transitions |
| § Studies of b → sγ Transitions |
| § Studies of b → dγ Transitions |
Measurements related to the CKM angle α ≡ φ2:
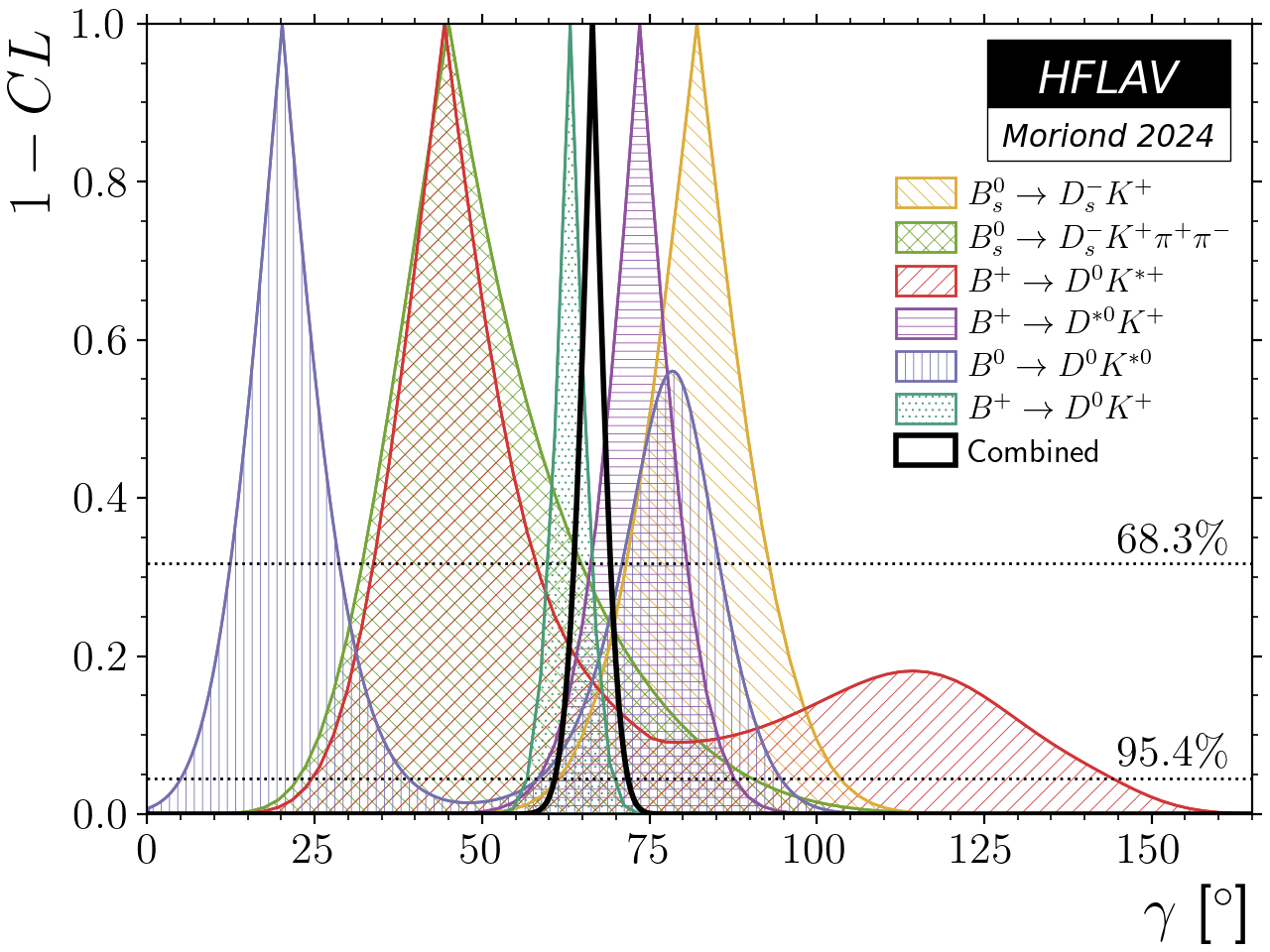
Measurements related to the CKM angle γ ≡ φ3:
| § Studies of Time-Dependent Interference Between b → cud and b → ucd Transitions |
| § Studies of Time-Dependent Interference Between b → cus and b → ucs Transitions |
§
Studies of Interference Between b → cus & b → ucs Transitions (also covering interference between b → cud & b → ucd transitions)
|
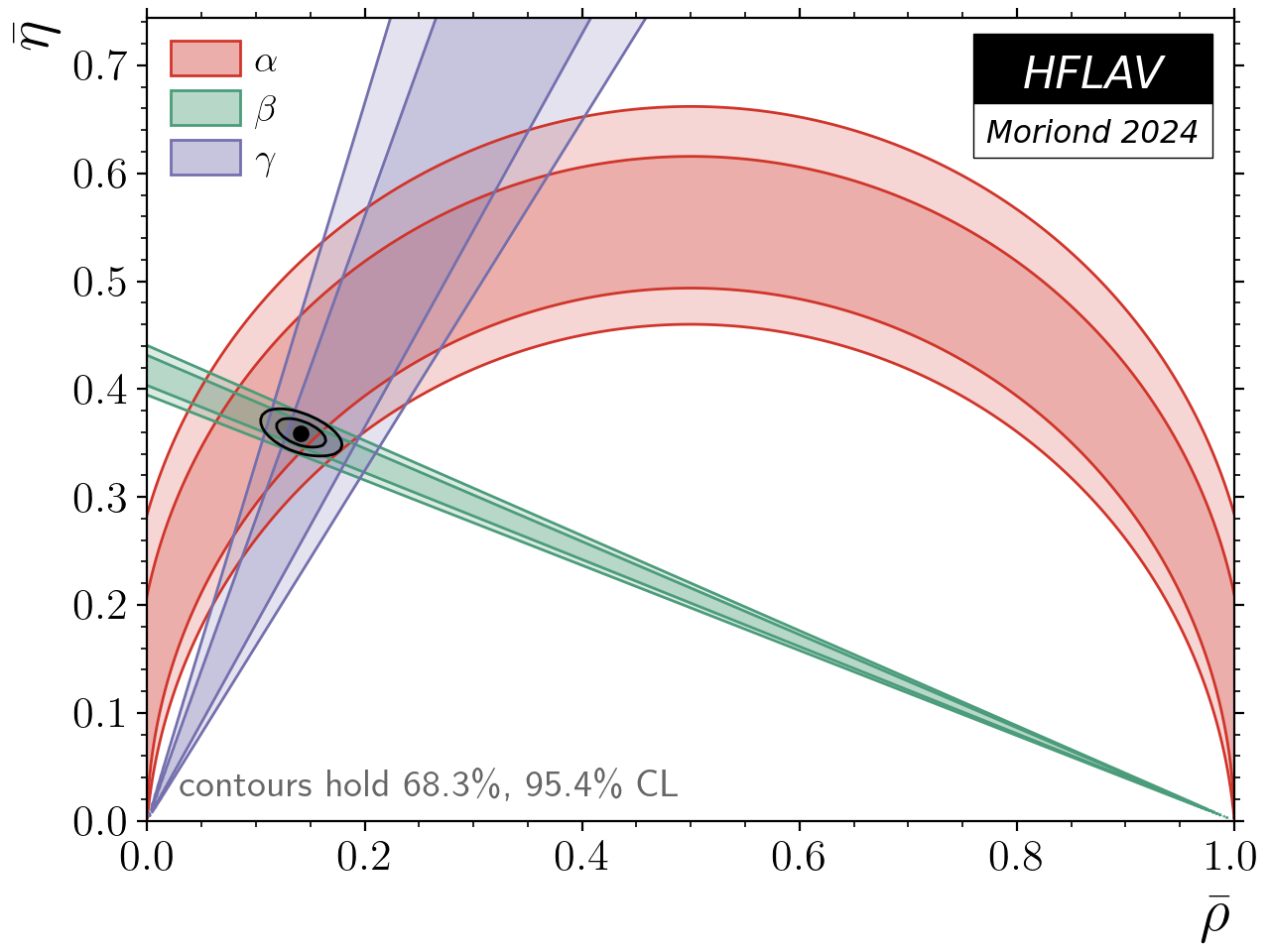
Summary of the constraints on Unitarity Triangle Angles
| § Plots Summarising the Obtained Constraints on the Angles of the Unitarity Triangle |
Legend: if not stated otherwise,
We use Combos v3.20 (homepage, manual) for the rescaling of the experimental results to common sets of input parameters.
The experimental results have been rescaled to a common set of input parameters (see table below).
| Parameter | Value | Reference |
|---|---|---|
| τ(Bd) | (1.519 ± 0.004) ps | HFLAV - Oscillations/Lifetime |
| Δmd | (0.5065 ± 0.0019) ps−1 | HFLAV - Oscillations/Lifetime |
| ΔΓd/Γd | 0.001 ± 0.010 | HFLAV - Oscillations/Lifetime |
|
|A⊥|2 (CP-odd fraction in B0→ J/ψK* CP sample) |
0.233 ± 0.010 ± 0.005 |
BaBar: PRD 76 (2007) 031102
N(BB)=232m |
| 0.195 ± 0.012 ± 0.008 |
Belle: PRL 95 (2005) 091601
N(BB)=275m |
|
| 0.215 ± 0.032 ± 0.006 |
CDF: PRL 94 (2005) 101803 (*)
∫Ldt=0.3 fb−1 |
|
| 0.183 ± 0.013 ± 0.025 |
D0: PRL 102 (2009) 032001
∫Ldt=2.8 fb−1 |
|
| 0.201 ± 0.004 ± 0.008 |
LHCb: PRD 88 (2013) 052002
∫Ldt=1.0 fb−1 |
|
| 0.209 ± 0.006 |
Average
χ2 = 7.2/4 dof (CL=0.12 ⇒ 1.5σ) |
(*) We do not include an unpublished CDF preliminary result from 2007.
Additional note on commonly treated (correlated) systematic effects:
We obtain for sin(2β) ≡ sin(2φ1) in the different decay modes:
| Parameter: sin(2β) ≡ sin(2φ1) | |||||
|---|---|---|---|---|---|
| Mode | BaBar | Belle | LHCb | Average | Reference |
| N(BB)=465M | N(BB)=772M | ∫Ldt=9 fb−1 | |||
| J/ψKS (ηCP=-1) (****) | 0.657 ± 0.036 ± 0.012 | 0.670 ± 0.029 ± 0.013 | 0.726 ± 0.014 (*) |
0.711 ± 0.012 (0.012stat-only) |
BaBar (PRD 79 (2009) 072009) Belle (PRL 108 (2012) 171802) LHCb (PRL 132 (2024) 021801, JHEP 11 (2017) 170) |
| J/ψKL (ηCP=+1) | 0.694 ± 0.061 ± 0.031 | 0.642 ± 0.047 ± 0.021 | - | 0.663 ± 0.041 (0.037stat-only) |
|
| J/ψK0 | 0.666 ± 0.031 ± 0.013 | - | - | 0.708 ± 0.012 (0.011stat-only) |
|
| ψ(2S)KS (ηCP=-1) | 0.897 ± 0.100 ± 0.036 | 0.738 ± 0.079 ± 0.036 |
0.84 ± 0.10 ± 0.01 0.649 ± 0.053 ± 0.018 (*) |
0.728 ± 0.038 (0.037stat-only) |
|
| ψ(nS)K0 | - | - | 0.724 ± 0.014 |
0.709 ± 0.012 (0.011stat-only) |
|
| χc1KS (ηCP=-1) | 0.614 ± 0.160 ± 0.040 | 0.640 ± 0.117 ± 0.040 | - | 0.632 ± 0.099 (0.094stat-only) |
|
| ηcKS (ηCP=-1) | 0.925 ± 0.160 ± 0.057 | - | - | - | BaBar (PRD 79 (2009) 072009) |
| J/ψK*0 (K*0 → KSπ0) (ηCP= 1-2|A⊥|2) | 0.601 ± 0.239 ± 0.087 | - | - | ||
| All charmonium | 0.687 ± 0.028 ± 0.012 | 0.667 ± 0.023 ± 0.012 | 0.724 ± 0.014 |
0.708 ± 0.011 (0.011stat-only) |
CL = 0.13 |
| χc0KS (ηCP=+1) |
0.69 ± 0.52 ± 0.04 ± 0.07 (**)
N(BB)=383M |
- | - | - | BaBar (PRD 80 (2009) 112001) |
| J/ψKS, J/ψ → hadrons (ηCP=+1) |
1.56 ± 0.42 ± 0.21 (***)
N(BB)=88M |
- | - | - | BaBar (PRD 69 (2004) 052001) |
| All charmonium (incl. χc0KS etc.) |
0.691 ± 0.031
(0.028stat-only) |
0.667 ± 0.023 ± 0.012 | 0.724 ± 0.014 |
0.709 ± 0.011 (0.011stat-only) |
CL = 0.11 |
(*)
The latest LHCb publication includes results for the J/ψKS and ψ(2S)KS final states obtained with LHC Run 2 data.
The paper also includes averages with their previous results, based on the Run 1 sample, for J/ψKS and J/ψKS+ψ(2S)KS combined.
Since there is no combined LHCb Run 1+2 result for ψ(2S)KS alone, we include the Run 1 and Run 2 results as separate inputs.
(**)
The BABAR result on χc0KS comes from the time-dependent Dalitz plot analysis of B0 → π+π−KS.
The third uncertainty is due to the Dalitz model.
(***)
BaBar (PRD 69 (2004) 052001) uses "hadronic and previously unused muonic decays of the J/ψ". We neglect a small possible correlation of this result with the main BaBar result that could be caused by reprocessing of the data.
(****)
Belle 2 have presented a first result with B0 → J/ψKS, measuring sin(2β) ≡ sin(2φ1) = 0.55 ± 0.21 ± 0.04, where the first uncertainty is statistical and the second is systematic. We do not include this result in our averages as it is not planned to be published. More recent preliminary results, as yet unsupported by publicly available documentation authored by the collaboration, are also not included.
Including earlier sin(2β) ≡ sin(2φ1) measurements, as well as a measurement by Belle using Υ(5S) data and B-π tagging:
| Parameter: sin(2β) ≡ sin(2φ1) | ||||
|---|---|---|---|---|
| Experiment | Value | Reference | ||
| ALEPH | 0.84 +0.82−1.04 ± 0.16 | PL B492 (2000) 259-274 | ||
| OPAL | 3.2 +1.8−2.0 ± 0.5 | EPJ C5 (1998) 379-388 | ||
| CDF (full Run I) | 0.79 +0.41−0.44(stat+syst) | PRD 61 (2000) 072005 | ||
| Belle (121/fb Υ(5S) data) | 0.57 ± 0.58 ± 0.06 | PRL 108 (2012) 171801 | ||
we find the slightly modified average:
| Parameter: sin(2β) ≡ sin(2φ1) | ||||
|---|---|---|---|---|
| All charmonium | 0.709 ± 0.011 (0.011stat-only) | CL = 0.26 | ||
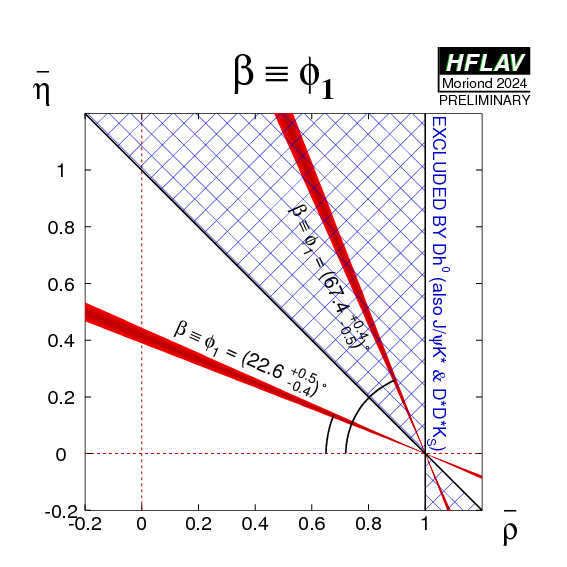
from which we obtain the following solutions for β ≡ φ1 (in [0, π])
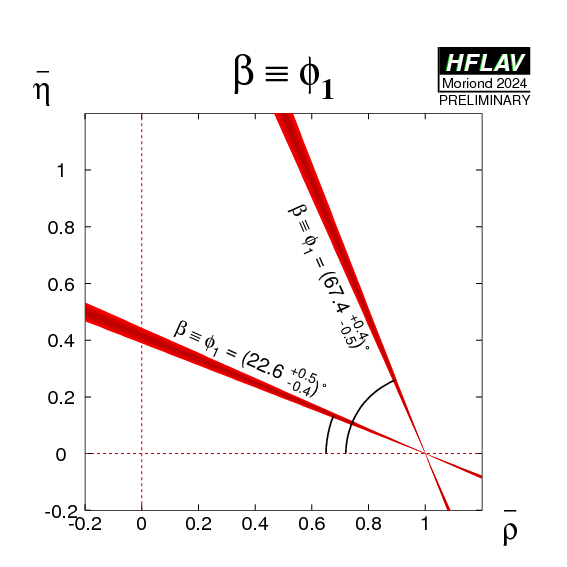
| β ≡ φ1 = (22.6 +0.5−0.4)° | or | β ≡ φ1 = (67.4 +0.4−0.5)° |
Plots:
| Averages of sin(2β) ≡ sin(2φ1) and C=−A from all experiments. |
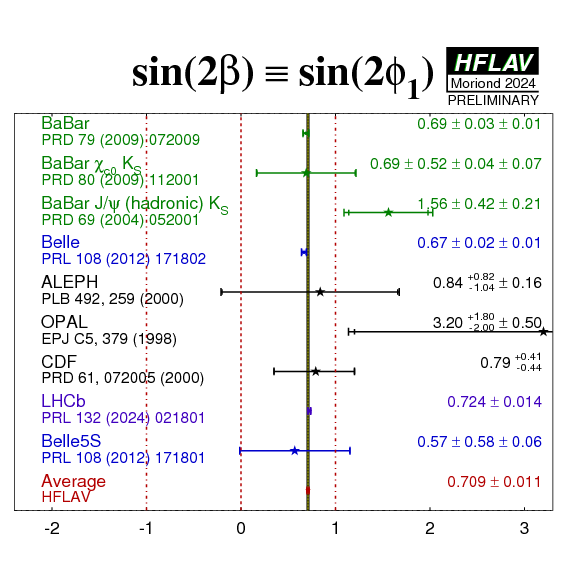
eps.gz png |

eps.gz png |
||
| Same, but excluding less precise results to allow closer inspection of the detail. |
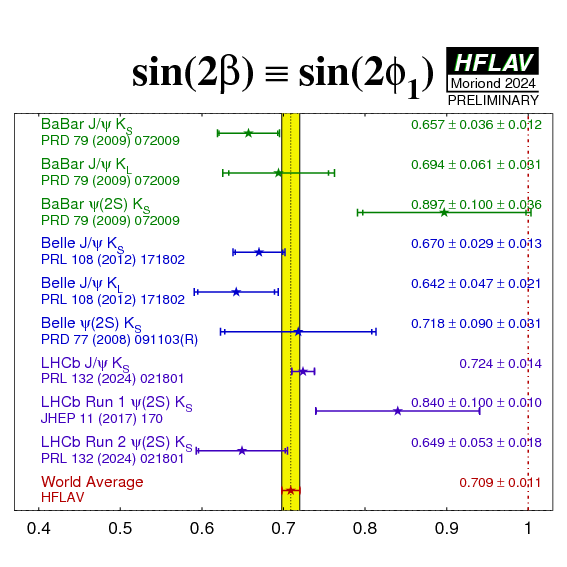
eps.gz png |
eps.gz png |
||
| Constraint on the ρ-bar-η-bar plane: |

eps.gz png |
eps.gz png |
||
|
Constraining the Unitarity Triangle (ρ, η):
Visit the CKMfitter and UTfit sites for results on global CKM fits using different fit techniques and input quantities. |
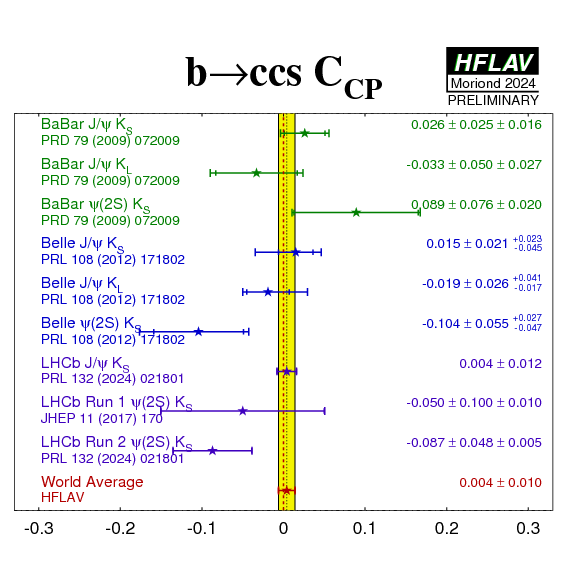
Historically the experiments determined |λ| for the charmonium modes; more recently the parameters C = −A = (1−|λ|2)/(1+|λ|2) are being used, as they are in all other time-dependent CP analyses. We recompute C from |λ| (from the BaBar results) for the following averages.
| Parameter: C=−A (if not stated otherwise) | |||||
|---|---|---|---|---|---|
| Mode | BaBar | Belle | LHCb | Average | Reference |
| N(BB)=465M | N(BB)=772M | ∫Ldt=9 fb−1 | |||
| J/ψKS | 0.026 ± 0.025 ± 0.016 | 0.015 ± 0.021 +0.023−0.045 | 0.010 ± 0.012 (†)(*) |
0.012 ± 0.011 (0.010stat-only) |
BaBar (PRD 79 (2009) 072009) Belle (PRL 108 (2012) 171802) LHCb (PRL 132 (2024) 021801, JHEP 11 (2017) 170) |
| J/ψKL | −0.033 ± 0.050 ± 0.027 | −0.019 ± 0.026 +0.041−0.017 | - | −0.023 ± 0.030 (0.023stat-only) |
|
| J/ψK0 | 0.016 ± 0.023 ± 0.018 | - | - |
0.009 ± 0.010 (0.009stat-only) |
|
| ψ(2S)KS | 0.089 ± 0.076 ± 0.020 | −0.104 ± 0.055 +0.027−0.047 |
−0.05 ± 0.10 ± 0.01 −0.087 ± 0.048 ± 0.005 |
−0.053 ± 0.034 (0.031stat-only) |
|
| ψ(nS)K0 | - | - | 0.004 ± 0.012 |
0.004 ± 0.010 (0.009stat-only) |
|
| χc1KS | 0.129 ± 0.109 ± 0.025 | 0.017 ± 0.083 +0.026−0.046 | - | 0.066 ± 0.074 (0.066stat-only) |
|
| ηcKS | 0.080 ± 0.124 ± 0.029 | - | - | - | BaBar (PRD 79 (2009) 072009) |
| J/ψK*0 (K*0 → KSπ0) | 0.025 ± 0.083 ± 0.054 | - | - | ||
| All charmonium | 0.024 ± 0.020 ± 0.016 | −0.006 ± 0.016 ± 0.012 | 0.004 ± 0.012 |
0.004 ± 0.010 (0.009stat-only) |
CL = 0.69 |
| χc0KS (ηCP=+1) | −0.29 +0.53−0.44 ± 0.03 ± 0.05 (**) | - | - | - | BaBar (PRD 80 (2009) 112001) |
| All charmonium (incl. χc0KS) | 0.023 ± 0.025 (0.020stat-only) |
−0.006 ± 0.016 ± 0.012 | 0.004 ± 0.012 |
0.004 ± 0.010 (0.009stat-only) |
CL = 0.69 |
(†)
The typical statistical correlation between S and C in LHCb measurements is 0.4–0.5, while those in e+e− → Υ(4S) B factories are close to zero.
These correlations are currently neglected in the averages.
(*)
The latest LHCb publication includes results for the J/ψKS and ψ(2S)KS final states obtained with LHC Run 2 data.
The paper also includes averages with their previous results, based on the Run 1 sample, for J/ψKS and J/ψKS+ψ(2S)KS combined.
Since there is no combined LHCb Run 1+2 result for ψ(2S)KS alone, we include both the Run 1 and Run 2 measurements as inputs.
(**)
The BABAR result on χc0KS comes from the time-dependent Dalitz plot analysis of B0 → π+π−KS.
The third uncertainty is due to the Dalitz model.
The BaBar and Belle collaborations have performed measurements of sin(2β) & cos(2β) ≡ sin(2φ1) & cos(2φ1) in time-dependent transversity analyses of the pseudoscalar to vector-vector decay B0→ J/ψK*, where cos(2β) ≡ cos(2φ1) enters as a factor in the interference between CP-even and CP-odd amplitudes. In principle, this analysis comes along with an ambiguity on the sign of cos(2β) ≡ cos(2φ1) due to an incomplete determination of the strong phases occurring in the three transversity amplitudes. BaBar resolves this ambiguity by inserting the known variation of the rapidly moving P-wave phase relative to the slowly moving S-wave phase with the invariant mass of the Kπ system in the vicinity of the K*(892) resonance. The result is in agreement with the prediction obtained from s-quark helicity conservation. It corresponds to Solution II defined by Suzuki, which is the phase convention used for the averages given here.
At present we do not apply a rescaling of the results to a common, updated set of input parameters.
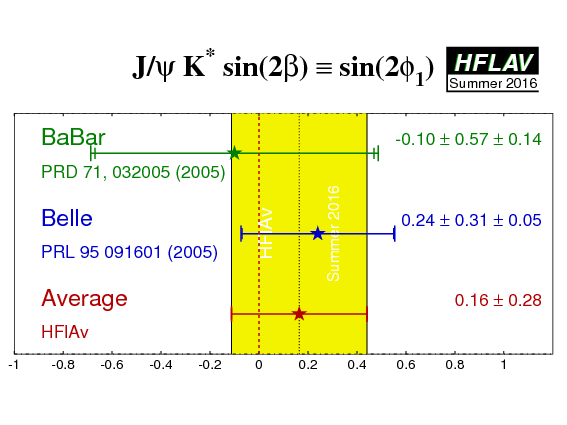
| Experiment | sin(2β) ≡ sin(2φ1)J/ψK* | cos(2β) ≡ cos(2φ1)J/ψK* | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=88M |
−0.10 ± 0.57 ± 0.14 | 3.32 +0.76 −0.96 ± 0.27 | −0.37 (stat) | PRD 71, 032005 (2005) |
|
Belle
N(BB)=275M |
0.24 ± 0.31 ± 0.05 |
0.56 ± 0.79 ± 0.11
[using Solution II] |
0.22 (stat) | PRL 95 091601 (2005) |
| Average |
0.16 ± 0.28
χ2 = 0.3/1 dof (CL = 0.61 → 0.5σ) |
1.64 ± 0.62
χ2 = 4.7/1 dof (CL = 0.03 → 2.2σ) |
uncorrelated averages |
HFLAV
See remark below table |
|
|
eps.gz png |

eps.gz png |
. | |
BaBar
find a confidence level for cos(2β)>0 of 89%.
Note that due to the strong non-Gaussian character of the BaBar measurement,
the interpretation of the average given above
has to be done with the greatest care.
We perform uncorrelated averages
(using the PDG prescription
for asymmetric errors).
The decays Bd → D(*)D(*)KS are dominated by the b → cc-bar s transition, and are therefore sensitive to 2β ≡ 2φ1. However, since the final state is not a CP eigenstate, extraction of the weak phases is difficult. Browder et al. have shown that terms sensitive to cos(2β) ≡ cos(2φ1) can be extracted from the analysis of Bd → D*D*KS decays (with some theoretical input).
Analysis of the Bd → D*D*KS decay has been performed by BaBar. and Belle.
The analyses proceed by dividing the Dalitz plot into two: m(D*+KS)2 > m(D*−KS)2 (ηy = +1) and m(D*+KS)2 < m(D*−KS)2 (ηy = -1). They then fit using a PDF where the time-dependent asymmetry (defined in the usual way as the difference between the time-dependent distributions of B0-tagged and B0-bar-tagged events, divided by their sum) is given by
| A(Δt) = ηy (Jc/J0) cos(ΔmdΔt) − [ (2Js1/J0)sin(2β) + ηy (2Js2/J0)cos(2β) ] sin(ΔmdΔt) |
The parameters J0, Jc, Js1 and Js2 are the integrals over the half-Dalitz plane m(D*+KS)2 < m(D*−KS)2 of the functions |a|2 + |a-bar|2, |a|2 - |a-bar|2, Re(a-bar a*) and Im(a-bar a*) respectively, where a and a-bar are the decay amplitudes of B0 → D*D*KS and B0-bar → D*D*KS respectively. The parameter Js2 (and hence Js2/J0) is predicted to be positive.
At present we do not apply a rescaling of the results to a common, updated set of input parameters.
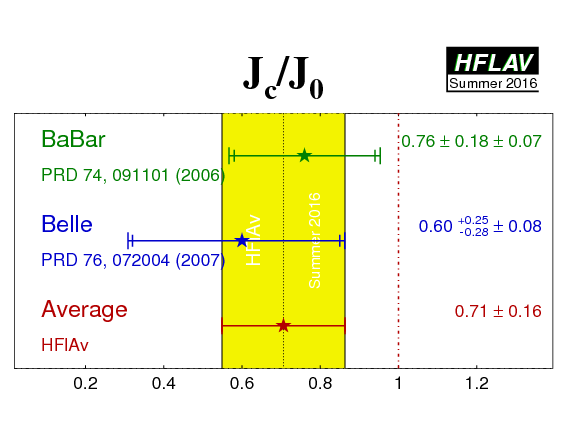
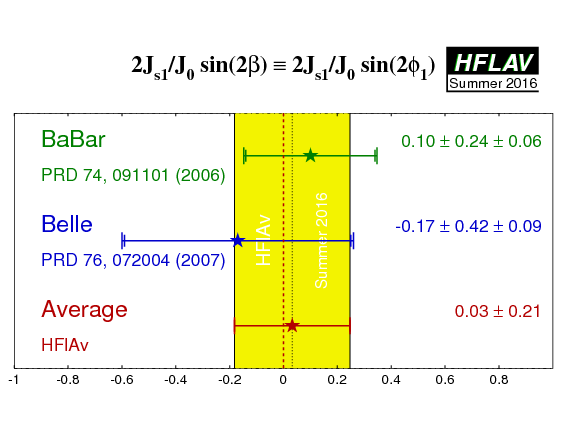
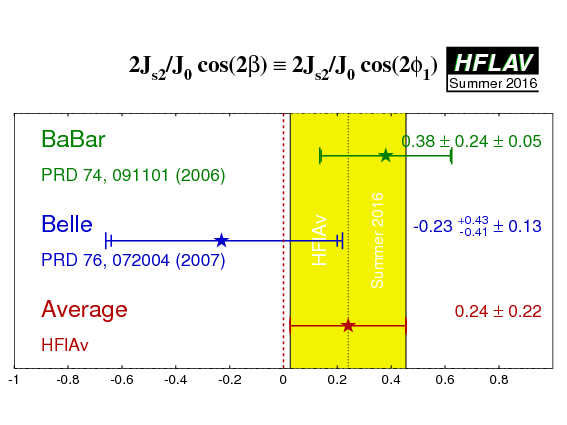
| Experiment | Jc/J0 | (2Js1/J0)sin(2β) ≡ (2Js1/J0)sin(2φ1) | (2Js2/J0)cos(2β) ≡ (2Js2/J0)cos(2φ1) | Correlation | Reference |
|---|---|---|---|---|---|
|
BaBar
N(BB)=230M |
0.76 ± 0.18 ± 0.07 | 0.10 ± 0.24 ± 0.06 | 0.38 ± 0.24 ± 0.05 | - | PRD 74, 091101 (2006) |
|
Belle
N(BB)=449M |
0.60 +0.25 −0.28 ± 0.08 | −0.17 ± 0.42 ± 0.09 | −0.23 +0.43 −0.41 ± 0.13 | - | PRD 76, 072004 (2007) |
| Average |
0.71 ± 0.16
χ2 = 0.2 (CL=0.63 ⇒ 0.5σ) |
0.03 ± 0.21
χ2 = 0.3 (CL=0.59 ⇒ 0.5σ) |
0.24 ± 0.22
χ2 = 1.4 (CL=0.23 ⇒ 1.2σ) |
uncorrelated averages | HFLAV |
|
|
eps.gz png |
eps.gz png |
eps.gz png |
. | |
From the above result and the assumption that Js2>0, BaBar infer that cos(2β)>0 at the 94% confidence level.
Decays of the Bs meson via the b → cc-bar s transition probe φs, a CP violating phase related to Bs–Bs-bar mixing. An important difference with respect to the Bd–Bd-bar system, is that the value of ΔΓ is predicted to significantly non-zero, allowing information on φs to be extracted without tagging the flavour of the decaying B meson. Within the Standard Model, φs is predicted to be very small, O(λ2).
The vector-vector final state J/ψ φ contains mixtures of polarization amplitudes: the CP-odd A⊥, and the CP-even A0 and A||. These terms need to be disentangled, using the angular distributions, in order to extract φs, and their interference provides additional sensitivity. The sensitivity to φs depends strongly on ΔΓ, and less strongly on the perpendicularly polarized fraction, |A⊥|2.
|
In this discussion we make the approximation φs ≈ −2βs where φs ≡ arg[ − M12 / Γ12 ] and 2βs ≡ 2 arg[ − VtsVtb* / VcsVcb* ]. This is a reasonable approximation since, although the equality does not hold in the Standard Model, both are much smaller than the current experimental resolution, whereas new physics contributions add a phase φNP to φs and subtract the same phase from 2βs, so that the approximation remains valid. |
Measurements of φs, based on flavour-tagged analyses of Bs → J/ψ φ decays, have been performed by ATLAS, CMS, CDF, D0 and LHCb. LHCb have in addition performed measurements of φs from Bs → J/ψ π+π−, Bs → J/ψ K+K− in the high m(K+K−) region, and Bs → Ds+Ds−.
Averaging of the above results is being carried out by the HFLAV lifetimes and oscillation group. Measurements related to φs in Bs → K+K−, Bs → φφ and K*0K*0 decays are reported below.
Bd decays to final states such as Dπ0 are governed by the b → cu-bar d transitions. If one chooses a final state which is a CP eigenstate, eg. DCPπ0, the usual time-dependence formulae are recovered, with the sine coefficient sensitive to sin(2β) ≡ sin(2φ1). Since there is no penguin contribution to these decays, there is even less associated theoretical uncertainty than for b → cc-bar s decays like Bd → J/ψ KS. See e.g. Fleischer, NPB 659 (2003) 321. Effects of subleading amplitudes ∝ Vub are expected to be negligible (~0.02) in the Standard Model, and to have opposite signs for the CP-even and CP-odd final states.
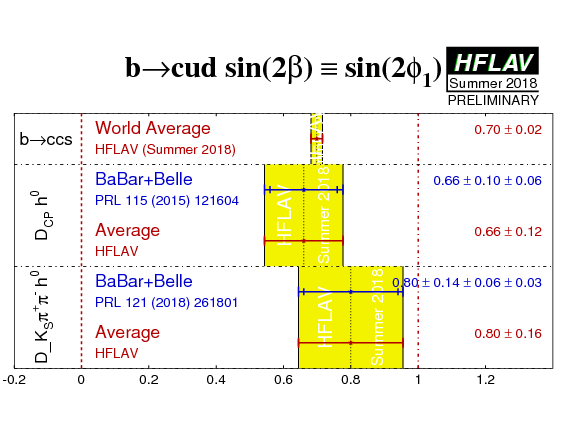
A joint analysis of the BaBar and Belle data samples has been performed to obtain to obtain the best determination of sin(2β) ≡ sin(2φ1) in these processes. All Bd → D(*)h0 decays are analysed together. The following CP-even final states are included: CP-even Dπ0 and Dη with D → KSπ0 and D → KSω, Dω with D → KSπ0, D*π0 and D*η with D* → Dπ0 and D → K+K−. The following CP-odd final states are included: Dπ0, Dη and Dω with D → K+K−, D*π0 and D*η with D* → Dπ0 and D → KSπ0.
| Mode | Experiment | sin(2β) ≡ sin(2φ1) | CCP | Correlation | Reference |
|---|---|---|---|---|---|
| D(*) h0 |
BaBar+Belle
N(BB)=1243M |
0.66 ± 0.10 ± 0.06 | −0.02 ± 0.07 ± 0.03 | −0.05 (stat) | PRL 115 (2015) 121604 |
Bondar, Gershon and Krokovny have shown that when multibody D decays, such as D → KSπ+π− are used, a time-dependent analysis of the Dalitz plot of the D decay allows a direct determination of the weak phase: β ≡ φ1. Equivalently, both sin(2β) ≡ sin(2φ1) and cos(2β) ≡ cos(2φ1) can be measured. This information allows to resolve the ambiguity in the measurement of 2β ≡ 2φ1 from sin(2β) ≡ sin(2φ1) alone. Simlarly to the case of Dalitz plot analysis of B− → DK− with D → KSπ+π−, such an analysis can be carried out with either model-dependent or model-independent methods.
A combined analysis of BaBar and Belle data has been done with the decays Bd → Dπ0, Bd → Dη, Bd → Dω, Bd → D*π0 and Bd → D*η are used. The daughter decays are D* → Dπ0, D → KSπ+π−, π0 → γγ, η → γγ and π+π−π0, and ω → π+π−π0. The D → KSπ+π− decay model is obtained from a fit to D*+ → D0π+ decays. The citation given in the table below corresponds to a Letter available as arXiv:1804.06152. A more detailed article on the same analysis is also available as arXiv:1804.06153. The results of this analysis supersede those from previous measurements by Belle and BaBar.
At present we do not apply a rescaling of the results to a common, updated set of input parameters. The third quoted uncertainty is due to Dalitz plot model dependence.
| Experiment | sin(2β) ≡ sin(2φ1) | cos(2β) ≡ cos(2φ1) | Correlations | Reference |
|---|---|---|---|---|
|
BaBar+Belle
N(BB)=1240M |
0.80 ± 0.14 ± 0.06 ± 0.03 | 0.91 ± 0.22 ± 0.09 ± 0.07 | 0.05 | PRL 121 (2018) 261801 |
Interpretations:
Treating β ≡ φ1 as a free parameter in the fit, the result β ≡ φ1 = (22.5 ± 4.4 ± 1.2 ± 0.6)° is obtained.
This corresponds to an observation of CP violation (β ≡ φ1 ≠ 0) at 5.1σ significance,
and evidence for cos 2β ≡ cos 2φ1 > 0 at 3.7σ.
The ambiguous solution with the value of sin 2β ≡ sin 2φ1 from b→cc-bar s transitions, but cos 2β ≡ cos 2φ1 < 0, is ruled out at 7.3σ
A model-independent analysis has been performed by Belle. The decays Bd → Dπ0, Bd → Dη, Bd → Dη′, Bd → Dω, Bd → D*π0 and Bd → D*η are used. Note that due to the strong statistical and systematic correlations, model-dependent results and model-independent results from the same experiment cannot be combined.
| Experiment | sin 2β | cos 2β | Correlation | Reference |
|---|---|---|---|---|
|
Belle
N(BB)=772M |
0.43 ± 0.27 ± 0.08 | 1.06 ± 0.33 +0.21 −0.15 | −0.03 (stat) | PR D94 (2016) 052004 |
Interpretations:
Belle
disfavour the solution with the charmonium-kaon value of sin(2φ)1 and a negative value for cos(2φ)1, at 5.1 σ significance.
The solution with the charmonium-kaon value of sin(2φ)1 and positive cos(2φ)1 is consistent with the data at the level of 1.3σ.
|
Compilation of results for
(left) sin(2βeff) ≡ sin(2φ1eff) = −ηCPS
from time-dependent b → cu-bar d analyses.
The model-dependent results for Bd → D(*)h0, D → KSπ+π− are used.
The results are compared
to the values from the corresponding charmonium-kaon averages.
The average value of sin(2β) ≡ sin(2φ1) in b → c ubar d transitions is
|
eps.gz png |
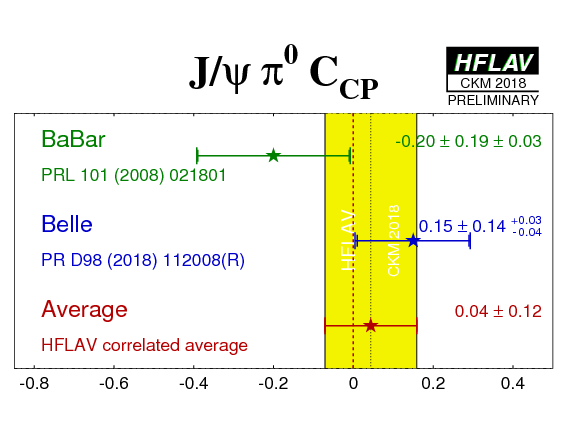
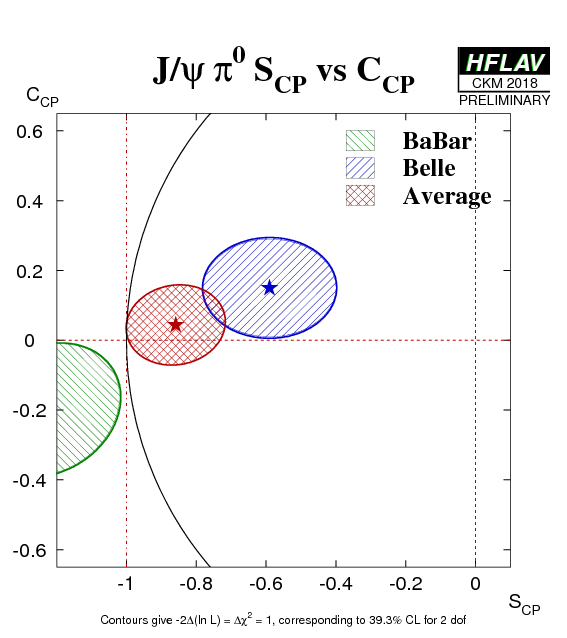
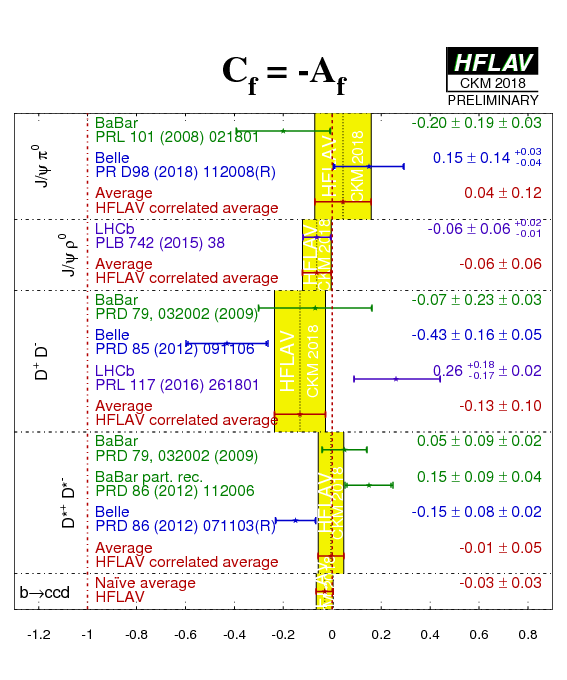
Due to possible significant penguin pollution, both the cosine and the sine coefficients of the Cabibbo-suppressed b → cc-bar d decays are free parameters of the theory. Absence of penguin pollution would result in Scc-bar d = − ηCP sin(2β) ≡ − ηCP sin(2φ1) and Ccc-bar d = 0 for the CP eigenstate final states (ηCP = +1 for both J/ψπ0 and D+D−).
At present we do not apply a rescaling of the results to a common, updated set of input parameters.
| Experiment | SCP (J/ψ π0) | CCP (J/ψ π0) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=466M |
−1.23 ± 0.21 ± 0.04 | −0.20 ± 0.19 ± 0.03 | 0.20 (stat) | PRL 101 (2008) 021801 |
|
Belle
N(BB)=772M |
−0.59 ± 0.19 ± 0.03 | 0.15 ± 0.14 +0.03 −0.04 | 0.01 (stat) | PR D98 (2018) 112008(R) |
| Average | −0.86 ± 0.14 | 0.04 ± 0.12 | 0.08 |
HFLAV correlated average
χ2 = 6.4/2 dof (CL=0.04 ⇒ 2.0σ) |
|
|

eps.gz png |
eps.gz png |
eps.gz png |
|
(*) Note that the BaBar result is outside of the physical region, and the average is very close to the boundary. The interpretation of the average given above has to be done with the greatest care.
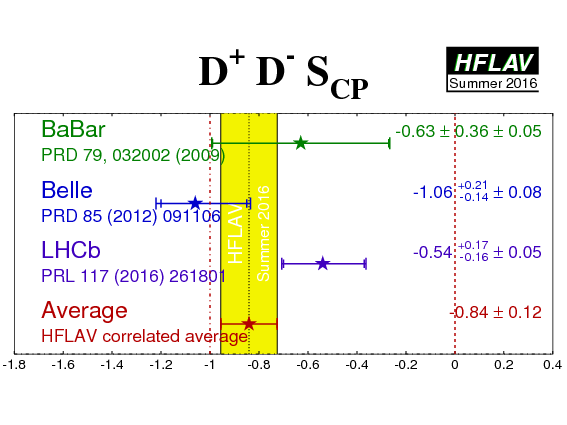
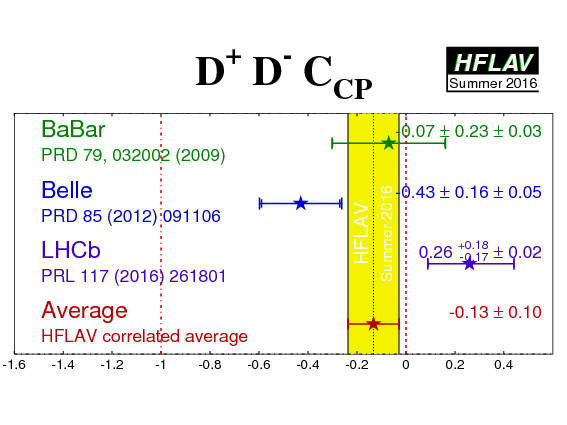
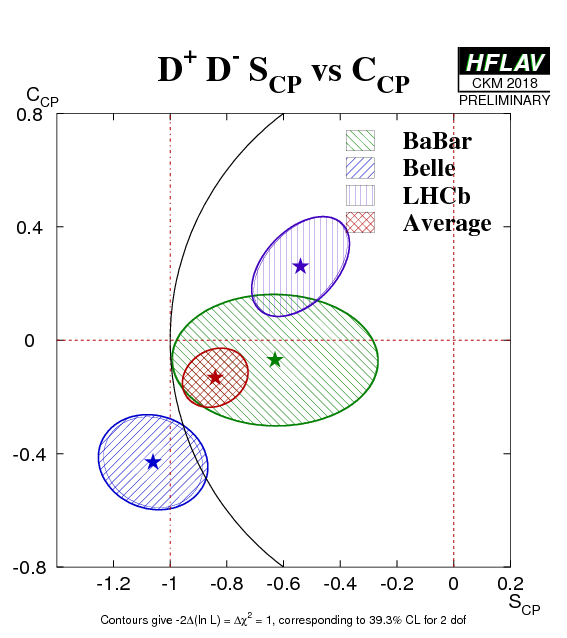
| Experiment | SCP (D+D−) | CCP (D+D−) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=467M |
−0.63 ± 0.36 ± 0.05 | −0.07 ± 0.23 ± 0.03 | −0.01 (stat) | PRD 79, 032002 (2009) |
|
Belle
N(BB)=772M |
−1.06 +0.21 −0.14 ± 0.08 | −0.43 ± 0.16 ± 0.05 | −0.12 (stat) | PRD 85 (2012) 091106 |
|
LHCb
∫Ldt=3 fb−1 |
−0.54 +0.17 −0.16 ± 0.05 | 0.26 +0.18 −0.17 ± 0.02 | 0.48 (stat) | PRL 117 (2016) 261801 |
| Average | −0.84 ± 0.12 | −0.13 ± 0.10 | 0.18 |
HFLAV correlated average
χ2 = 11/4 dof (CL=0.027 ⇒ 2.2σ) |
|
|
eps.gz png |
eps.gz png |
eps.gz png |
|
(*) Note that the Belle result is outside of the physical region, and the average is very close to the boundary. The interpretation of the average given above has to be done with the greatest care.
The vector-vector final states J/ψρ0 and D*+D*− are mixtures of CP-even and CP-odd; the longitudinally polarized component is CP-even. Note that in the general case of non-negligible penguin contributions, the penguin-tree ratio and strong phase differences do not have to be the same for each helicity amplitude (likewise, they do not have to be the same for D*+D− and D*−D+).
Different techniques have been used to study these two VV modes. LHCb has performed a full time-dependent amplitude analysis of B0 → J/ψπ+π- decays, find a J/ψρ0 fit fraction of 65% and a longitudinal polarisation fraction of 57% (both consistent with results from a time-integrated amplitude analysis). Fits are performed to obtain 2βeff in the cases that all transversity amplitudes are assumed to have the same CP violation parameter, and allowing different parameters. The results in the former case are presented in terms of SCP and CCP below.
| Experiment | SCP (J/ψ ρ0) | CCP (J/ψ ρ0) | Correlation | Reference |
|---|---|---|---|---|
|
LHCb
∫Ldt=3 fb−1 |
−0.66 +0.13 −0.12 +0.09 −0.03 | −0.06 ± 0.06 +0.02 −0.01 | −0.01 (stat) | PLB 742 (2015) 38 |
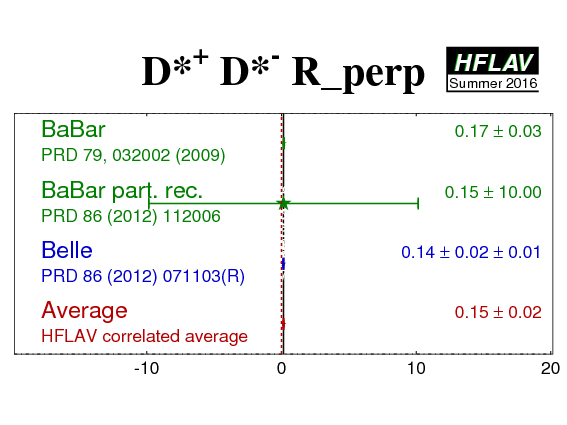
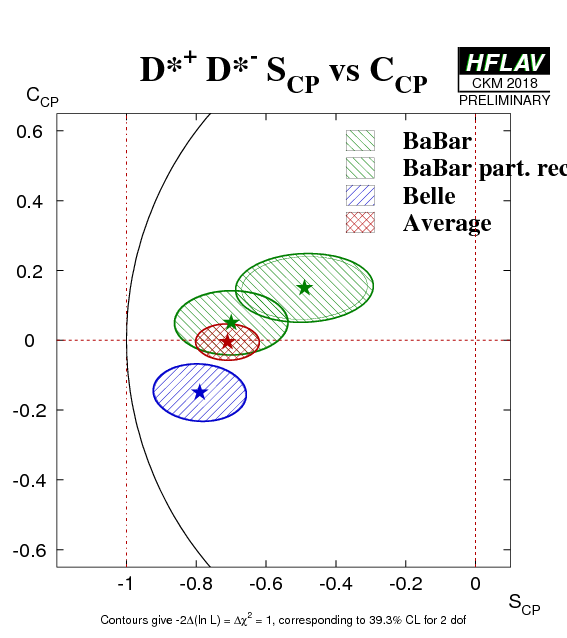
The vector particles in the pseudoscalar to vector-vector decay Bd → D*+D*− can have longitudinal and transverse relative polarization with different CP properties. The transversely polarized state (h⊥) is CP-odd, while the other two states in the transversity basis (h0 and h||) are CP-even. The CP parameters therefore have an important dependence on the fraction of the transversely polarized component R⊥.
In the most recent results, Belle performs an initial fit to determine the transversely polarized fraction R⊥, and then include effects due to its uncertainty together with other systematic errors. (In the most recent update Belle include R⊥ and also R0 as free parameters in the fit. We do not include information on R0 in the average for now.) BaBar treat R⊥ as a free parameter in the fit and consequently this systematic is absorbed in the statistical error. We perform the average taking into account correlations of the CP parameters with each other as well as with R⊥.
Belle have performed a fit to the data assuming that the CP parameters for CP-even and CP-odd transversity states are the same (up to a trivial change of sign for SCP). BaBar have performed two fits to the data: in addition to a fit as above, an additional fit relaxes this assumption, so that differences between CP-even and CP-odd parameters may be nontrivial. We use the first set of results to perform an average with Belle, and tabulate also the latter set of results. We also include the results of a separate analysis from BaBar based on partially reconstructed D*D* decays; in this analysis the BaBar measurement of R⊥ is used to correct the value of S fitted without separating CP-even and -odd components for the CP-odd dilution.
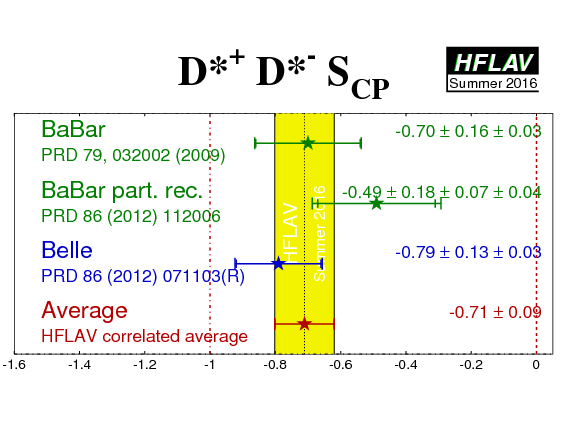
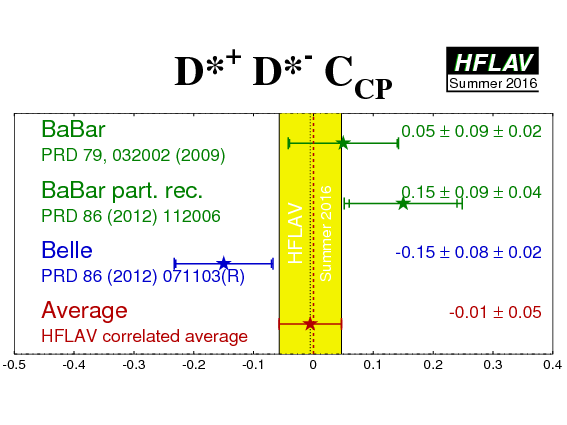
| Experiment | SCP (D*+ D*−) | CCP (D*+ D*−) | R⊥ (D*+ D*−) | Correlation | Reference |
|---|---|---|---|---|---|
|
BaBar
N(BB)=467M |
−0.70 ± 0.16 ± 0.03 | 0.05 ± 0.09 ± 0.02 | 0.17 ± 0.03 | (stat) | PRD 79, 032002 (2009) |
|
BaBar part. rec.
N(BB)=471M |
−0.49 ± 0.18 ± 0.07 ± 0.04 | 0.15 ± 0.09 ± 0.04 | - | (stat) | PRD 86 (2012) 112006 |
|
Belle
N(BB)=772M |
−0.79 ± 0.13 ± 0.03 | −0.15 ± 0.08 ± 0.02 | 0.14 ± 0.02 ± 0.01 | (stat) | PRD 86 (2012) 071103(R) |
| Average | −0.71 ± 0.09 | −0.01 ± 0.05 | 0.15 ± 0.02 | (stat) |
HFLAV correlated average
χ2 = 3.7/6 dof (CL=0.72 ⇒ 0.4σ) |
|
|
eps.gz png |
eps.gz png |
eps.gz png |
eps.gz png |
|
| Experiment | S+ (D*+ D*−) | C+ (D*+ D*−) | S− (D*+ D*−) | C− (D*+ D*−) | R⊥ (D*+ D*−) | Correlation | Reference |
|---|---|---|---|---|---|---|---|
|
BaBar
N(BB)=467M |
−0.76 ± 0.16 ± 0.04 | 0.02 ± 0.12 ± 0.02 | −1.81 ± 0.71 ± 0.16 | 0.41 ± 0.50 ± 0.08 | 0.15 ± 0.03 | (stat) | PRD 79, 032002 (2009) |
(*) Note that the BaBar values of R⊥ in these tables are not corrected for efficiency; the efficiency corrected value is R⊥ = 0.158 ± 0.028 ± 0.006.
For the non-CP eigenstates D*+−D−+, absence of penguin pollution (ie. no direct CP violation) gives A = 0, C+ = −C− (but is not necessarily zero), S+ = 2 R sin(2β+δ)/(1+R2) and S− = 2 R sin(2β−δ)/(1+R2). [With alternative notation, S+ = 2 R sin(2φ1+δ)/(1+R2) and S− = 2 R sin(2φ1−δ)/(1+R2)]. Here R is the ratio of the magnitudes of the amplitudes for B0 → D*+D− and B0 → D*−D+, while δ is the strong phase between them. If there is no CP violation of any kind, then S+ = −S− (but is not necessarily zero). An alternative notation, S = (S+ + S−)/2, Δ S = (S+ −S−)/2, C = (C+ + C−)/2, Δ C = (C+ −C−)/2, has been used in recent publications.
| Experiment | S(D*+D−) | C(D*+D−) | ΔS(D*−D+) | ΔC(D*−D+) | A(D*+−D−+) | Correlation | Reference |
|---|---|---|---|---|---|---|---|
|
BaBar
N(BB)=467M |
−0.68 ± 0.15 ± 0.04 | 0.04 ± 0.12 ± 0.03 | 0.05 ± 0.15 ± 0.02 | 0.04 ± 0.12 ± 0.03 | 0.01 ± 0.05 ± 0.01 | - | PRD 79, 032002 (2009) |
|
Belle
N(BB)=772M |
−0.78 ± 0.15 ± 0.05 | −0.01 ± 0.11 ± 0.04 | −0.13 ± 0.15 ± 0.04 | 0.12 ± 0.11 ± 0.03 | 0.06 ± 0.05 ± 0.02 | - | PRD 85 (2012) 091106 |
|
LHCb
∫Ldt=9 fb−1 |
−0.86 ± 0.08 ± 0.02 | −0.06 ± 0.09 ± 0.02 | 0.02 ± 0.07 ± 0.01 | −0.03 ± 0.09 ± 0.02 | 0.01 ± 0.01 ± 0.01 | (stat) | JHEP 2003 (2020) 147 |
| Average | −0.81 ± 0.06 | −0.01 ± 0.06 | 0.02 ± 0.06 | 0.03 ± 0.06 | 0.01 ± 0.01 | (stat) |
HFLAV correlated average
χ2 = 4.4/10 dof (CL=0.93 ⇒ 0.1σ) |
|
|
eps.gz png | eps.gz png | eps.gz png | eps.gz png | eps.gz png | . | |
| Compilation of results for (left) sin(2βeff) ≡ sin(2φ1eff) = −ηCPS and (right) C ≡ −A from time-dependent b → cc-bar d analyses with CP eigenstate final states. The results are compared to the values from the corresponding charmonium averages. |

eps.gz png |

eps.gz png |
||||
| Same, but with separate CP-even and CP-odd results from D*+D*− |
|
|
||||
|
Same, but including results from
D*+−D−+.
(These measure the same quantity as other b → cc-bar d modes when the strong phase difference between the two decay amplitudes vanishes. This is in addition to the usual assumption of negligible penguin contributions.) |
|
|
||||
Same, but including a naïve b → c c-bar d average.
Such an average assumes that penguin contributions to the
b → c c-bar d decays are negligible.
See the cautionary comments in the discussion on averaging
the time-dependent CP violation parameters for
b → qq-bar s transitions above.
The results of the naïve average are
|

eps.gz png |
eps.gz png |
||||
| 2D comparisons of averages in the different b→c c-bar d modes. |

eps png |
|||||
Time-dependent CP asymmetries in Bs decays mediated by b → cc-bar d transitions provide a determination of φseff where possible effects from penguin amplitudes may cause a shift from the value of φs seen in b → cc-bar s transitions. Results in the b → cc-bar d case, with larger penguin effects, can be used together with flavour symmetries to derive limits on the possible size of penguin effects in the b → cc-bar s transitions, as described by Fleischer et al. (hep-ph/9903455, arXiv:1010.0089). If the penguin effect is large, it may also be possible to determine γ ≡ φ3.
The parameters have been measured in Bs → J/ψ KS0 decays by LHCb.
| Experiment | SCP | CCP | AΔΓ | Correlation | Reference |
|---|---|---|---|---|---|
|
LHCb
∫Ldt=3 fb−1 |
0.49 +0.77 −0.65 ± 0.06 | −0.28 ± 0.41 ± 0.08 | −0.08 ± 0.40 ± 0.08 | (stat) | JHEP 06 (2015) 131 |
Within the Standard Model, the b → s penguin transition carries approximately the same weak phase as the b → cc-bar s amplitude used above to obtain sin(2β) ≡ sin(2φ1). When this single phase dominates the decay to a (quasi-)two-body CP eigenstate, the time-dependent CP violation parameters should therefore by given by S = −ηCP × sin(2βeff) ≡ −ηCP × sin(2φ1eff) and C ≡ −A = 0. The loop process is sensitive to effects from virtual new physics particles, which may result in deviations from the prediction that sin(2βeff) ≡ sin(2φ1eff) (b → qq-bar s) ∼ sin(2β) ≡ sin(2φ1) (b → cc-bar s).
Various different final states have been used by BaBar and Belle to investigate time-dependent CP violation in hadronic b → s penguin transitions. These are summarised below. (Note that results from time-dependent Dalitz plot analyses of B0 → K+K−K0 and B0 → π+π−KS are also discussed in the next section — results for φK0, ρ0KS and f0KS are extracted from these analyses. The third error, where given, is due to Dalitz model uncertainty.)
At present we do not apply a rescaling of the results to a common, updated set of input parameters. We take correlations between S and C into account where available, except if one or more of the measurements suffers from strongly non-Gaussian errors. In that case, we perform uncorrelated averages (using the PDG prescription for asymmetric errors).
| Mode | Experiment | sin(2βeff) ≡ sin(2φ1eff) | CCP | Correlation | Reference |
|---|---|---|---|---|---|
| φK0 |
BaBar
(*)
N(BB)=470M |
0.66 ± 0.17 ± 0.07 | 0.05 ± 0.18 ± 0.05 | - | PRD 85 (2012) 112010 |
|
Belle
(*)
N(BB)=657M |
0.90 +0.09 −0.19 | −0.04 ± 0.20 ± 0.10 ± 0.02 | - | PRD 82 (2010) 073011 | |
|
Belle II
N(BB)=387M |
0.54 ± 0.26 +0.06 −0.08 | −0.31 ± 0.20 ± 0.05 | 0.01 (stat) | PRD 108 (2023) 072012 | |
| Average (*) |
0.74 ± 0.12
χ2 = 1.5/2 dof (CL=0.46 ⇒ 0.7σ) |
−0.09 ± 0.12
χ2 = 1.7/2 dof (CL=0.42 ⇒ 0.8σ) |
- | HFLAV | |
|
|
eps.gz png | eps.gz png | . | ||
| η′K0 |
BaBar
N(BB)=467M |
0.57 ± 0.08 ± 0.02 | −0.08 ± 0.06 ± 0.02 | 0.03 (stat) | PRD 79 (2009) 052003 |
|
Belle
N(BB)=772M |
0.68 ± 0.07 ± 0.03 | −0.03 ± 0.05 ± 0.03 | 0.03 (stat) | JHEP 1410 (2014) 165 | |
|
Belle II
N(BB)=387M |
0.67 ± 0.10 ± 0.04 | −0.19 ± 0.08 ± 0.03 | 0.03 (stat) | arXiv:2402.03713 | |
| Average | 0.64 ± 0.05 | −0.08 ± 0.04 | 0.02 |
HFLAV correlated average
χ2 = 3.5/4 dof (CL=0.48 ⇒ 0.7σ) |
|
|
|
eps.gz png | eps.gz png | eps.gz png | ||
| KSKSKS |
BaBar
N(BB)=468M |
0.94 +0.21 −0.24 ± 0.06 | −0.17 ± 0.18 ± 0.04 | 0.16 (stat) | PRD 85 (2012) 054023 |
|
Belle
N(BB)=722M |
0.71 ± 0.23 ± 0.05 | −0.12 ± 0.16 ± 0.05 | - | PRD 103 (2021) 032003 | |
| Average | 0.83 ± 0.17 | −0.15 ± 0.12 | 0.07 |
HFLAV correlated average
χ2 = 0.55/2 dof (CL=0.76 ⇒ 0.3σ) |
|
|
|
eps.gz png | eps.gz png | eps.gz png | ||
| π0K0 |
BaBar
N(BB)=467M |
0.55 ± 0.20 ± 0.03 | 0.13 ± 0.13 ± 0.03 | 0.06 (stat) | PRD 79 (2009) 052003 |
|
Belle
N(BB)=657M |
0.67 ± 0.31 ± 0.08 | −0.14 ± 0.13 ± 0.06 | −0.04 (stat) | PRD 81 (2010) 011101 | |
|
Belle II
(****)
N(BB)=387M |
0.75 +0.20 −0.23 ± 0.04 | −0.04 +0.14 −0.15 ± 0.05 | −0.00 (stat) | PRL 131 (2023) 111803 | |
| Average | 0.64 ± 0.13 | −0.01 ± 0.08 | 0.02 |
HFLAV correlated average
χ2 = 2.5/4 dof (CL=0.65 ⇒ 0.5σ) |
|
|
|
eps.gz png | eps.gz png | eps.gz png | ||
| ρ0KS |
BaBar
(*)
N(BB)=383M |
0.35 +0.26 −0.31 ± 0.06 ± 0.03 | −0.05 ± 0.26 ± 0.10 ± 0.03 | - | PRD 80 (2009) 112001 |
|
Belle
(*)
N(BB)=657M |
0.64 +0.19 −0.25 ± 0.09 ± 0.10 | −0.03 +0.24 −0.23 ± 0.11 ± 0.10 | - | PRD 79 (2009) 072004 | |
| Average | 0.54 +0.18 −0.21 | −0.06 ± 0.20 | - | HFLAV | |
|
|
eps.gz png | eps.gz png | . | ||
| ωKS |
BaBar
N(BB)=467M |
0.55 +0.26 −0.29 ± 0.02 | −0.52 +0.22 −0.20 ± 0.03 | 0.03 (stat) | PRD 79 (2009) 052003 |
|
Belle
N(BB)=772M |
0.91 ± 0.32 ± 0.05 | 0.36 ± 0.19 ± 0.05 | −0.00 (stat) | PRD 90 (2014) 012002 | |
| Average | 0.71 ± 0.21 | −0.04 ± 0.14 | 0.01 |
HFLAV correlated average
χ2 = 9.9/2 dof (CL=0.007 ⇒ 2.7σ) |
|
|
|
eps.gz png | eps.gz png | eps.gz png | ||
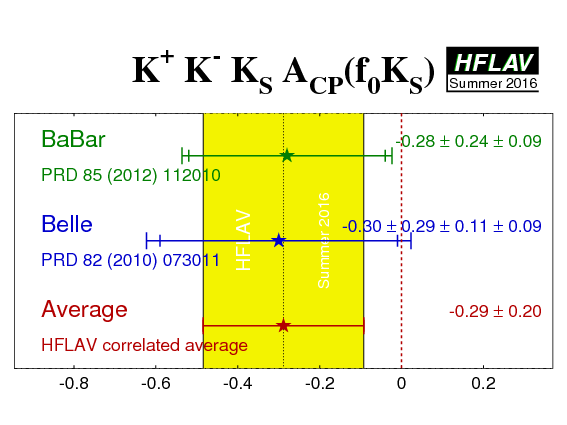
| f0K0 | BaBar (**) | 0.74 +0.12 −0.15 | 0.15 ± 0.16 | - | HFLAV (**) |
| Belle (**) | 0.63 +0.16 −0.19 | 0.13 ± 0.17 | - | HFLAV (**) | |
| Average | 0.69 +0.10 −0.12 | 0.14 ± 0.12 | - | HFLAV | |
|
|
eps.gz png | eps.gz png | . | ||
| f2KS |
BaBar
(*)
N(BB)=383M |
0.48 ± 0.52 ± 0.06 ± 0.10 | 0.28 +0.35 −0.40 ± 0.08 ± 0.07 | 0.01 (stat) | PRD 80 (2009) 112001 |
| fXKS |
BaBar
(*)
N(BB)=383M |
0.20 ± 0.52 ± 0.07 ± 0.07 | 0.13 +0.33 −0.35 ± 0.04 ± 0.09 | 0.29 (stat) | PRD 80 (2009) 112001 |
| π0π0KS |
BaBar
N(BB)=227M |
−0.72 ± 0.71 ± 0.08 | 0.23 ± 0.52 ± 0.13 | −0.02 (stat) | PRD 76 (2007) 071101 |
|
Belle
N(BB)=772M |
0.92 +0.27 −0.31 ± 0.11 | −0.28 ± 0.21 ± 0.04 | 0.00 (stat) | PR D99 (2019) 011102 | |
| Average | 0.66 ± 0.28 | −0.21 ± 0.20 | −0.00 |
HFLAV correlated average
χ2 = 5.2/2 dof (CL=0.08 ⇒ 1.8σ) |
|
|
|
eps.gz png | eps.gz png | eps.gz png | ||
| φ KS π0 |
BaBar
(***)
N(BB)=465M |
0.97 +0.03 −0.52 | −0.20 ± 0.14 ± 0.06 | - | PRD 78 (2008) 092008 |
| π+ π− KS nonresonant |
BaBar
(*)
N(BB)=383M |
0.01 ± 0.31 ± 0.05 ± 0.09 | 0.01 ± 0.25 ± 0.06 ± 0.05 | −0.11 (stat) | PRD 80 (2009) 112001 |
|
K+K−K0
(excluding φK0 and f0K0) |
BaBar
(*)
N(BB)=470M |
0.65 ± 0.12 ± 0.03 | 0.02 ± 0.09 ± 0.03 | - | PRD 85 (2012) 112010 |
|
Belle
(*)
N(BB)=657M |
0.76 +0.14 −0.18 | 0.14 ± 0.11 ± 0.08 ± 0.03 | - | PRD 82 (2010) 073011 | |
| Average | 0.68 +0.09 −0.10 |
0.06 ± 0.08
|
- | HFLAV | |
|
|
eps.gz png | eps.gz png | . | ||
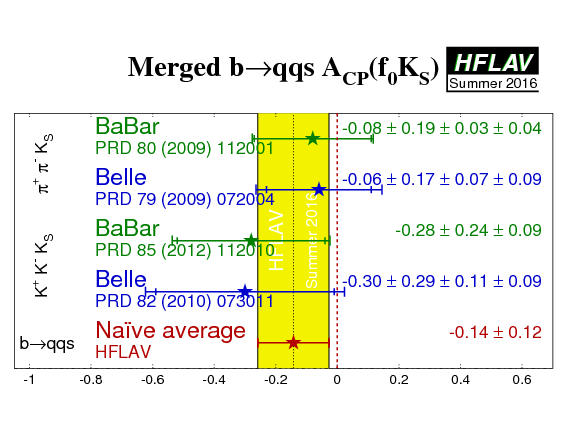
| Naïve b→s penguin average |
0.654 ± 0.037
χ2 = 17/21 dof (CL=0.69 ⇒ 0.4σ) |
−0.003 ± 0.029
χ2 = 20/21 dof (CL=0.52 ⇒ 0.7σ) |
uncorrelated averages | HFLAV | |
| eps.gz png | eps.gz png | ||||
| Direct comparison of charmonium and s-penguin averages (see comments below): χ2 = 1.2 (CL=0.27 ⇒ 1.1σ) | |||||
(*)
BaBar and Belle results for φK0,
ρ0KS and
K+K−K0 (excluding φK0 and f0K0)
are determined from their
time-dependent Dalitz plot analyses of
B0 → K+K−K0 and
B0 → π+π−KS.
For the experimental results,
we quote Q2B parameters that are given in the respective references,
where possible.
(Belle have not reported Q2B S parameters from their
time-dependent Dalitz plot analysis of
B0 → K+K−KS,
so we convert their results on φ1.)
The averages of the directly fitted parameters
are more reliable than those of the Q2B parameters,
therefore where possible we convert those results to give the averages quoted in the
table above.
BaBar results for f2KS,
fXKS and
π+ π− KS nonresonant
are determined from their
time-dependent Dalitz plot analysis of
B0 → π+π−KS.
(**) BaBar and Belle results for f0K0 are combinations of results from the two Dalitz plot analyses: B0 → f0K0 with f0 → K+K−, and B0 → f0KS with f0 → π+π−. Note that Q2B parameters extracted from Dalitz plot analyses are constrained to lie within the physical boundary (SCP2 + CCP2 < 1), and consequently the obtained errors can be highly non-Gaussian when the central value is close to the boundary. This is particularly evident in the BaBar results from B0 → f0KS with f0 → π+π−. These results must be treated with extreme caution. As above, we convert the averages of the directly fitted parameters from the time-dependent Dalitz plot analyses back to the Q2B parameters given in the table above.
(***) The BaBar results on φ KS π0 come from a simultaneous angular analysis of B → φ K+ π− and B → φ KS π0, where the angular parameters of the two decays modes are related since only (Kπ) resonances contribute to the final state. Note that Q2B parameters extracted in this way are constrained to lie within the physical boundary (SCP2 + CCP2 < 1), and consequently the obtained errors are highly non-Gaussian when the central value is close to the boundary. The single uncertainty given for sin(2βeff) in this result includes both statistical and systematic uncertainties.
(****) The results presented here are from a Belle II time-dependent analysis. They have additionally published results from a time-integrated analysis of B0 → π0KS decays, which also provides sensitivity to ACP =-CCP. The time-integrated results are not included here.
Please note that
| Compilation of results for −η×S ≈ sin(2βeff) ≡ sin(2φ1eff) and C from s-penguin decays. |

eps png |
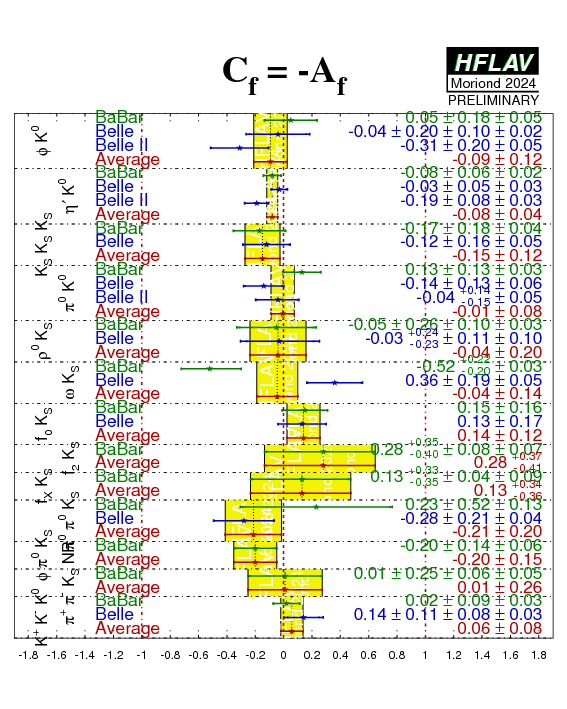
eps png |
| Same, but without less precise results to allow closer inspection of the detail. |
|
|
| Comparisons of averages in the different b→q q-bar s modes |
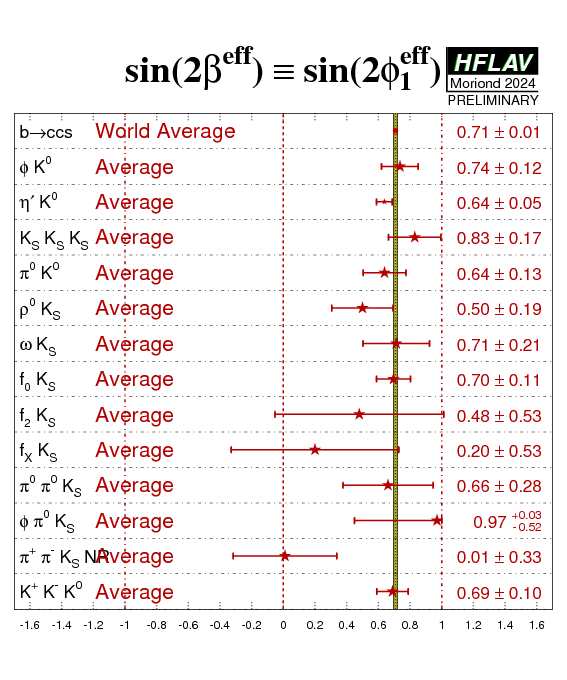
eps png |

eps png |
| Same, but without f2KS, fXKS π0π0KS, π+ π− KS nonresonant and φ KS π0 to allow closer inspection of the detail. |
|
|
| 2D comparisons of averages in the different b→q q-bar s modes. |
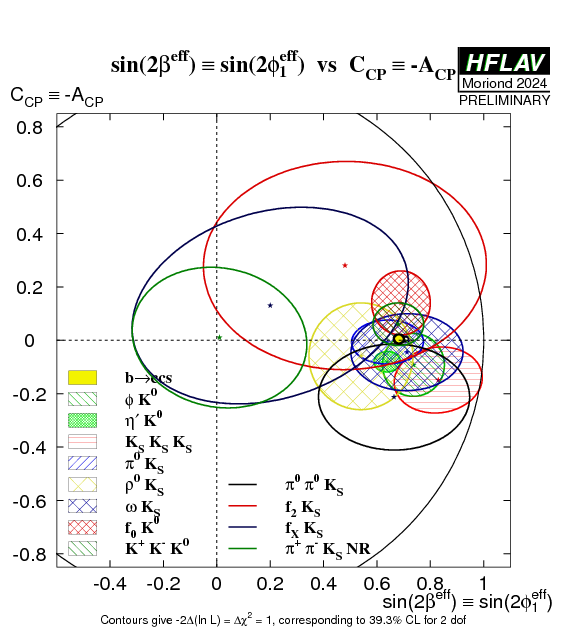
eps png |
|
| Same, but without less precise results to allow closer inspection of the detail. |
|
|
Time-dependent amplitude analyses of the three-body decays Bd → K+K−K0 and Bd → π+π−K0 allow additional information to be extracted from the data. In particular, the cosine of the effective weak phase difference (cos(2βeff) ≡ cos(2φ1eff)) can be determined, as well as the sine term that is obtained from quasi-two-body analysis. This information allows half of the degenerate solutions to be rejected. Furthermore, Dalitz plot analysis has enhanced sensitivity to direct CP violation.
Time-dependent Dalitz plot analyses of B0 → K+K−KS have been performed by BaBar and Belle. As given above, parameters can be extracted in a form that allows a straightforward comparison/combination with those from time-dependent CP asymmetries in quasi-two-body b → qq-bar s modes. In addition, the effective weak phase βeff ≡ φ1eff is directly determined for two significant resonant contributions: φK0 and f0K0 and for the rest of the charmless contributions to the Dalitz plot combined, with the CP properties of the individual components taken into account.
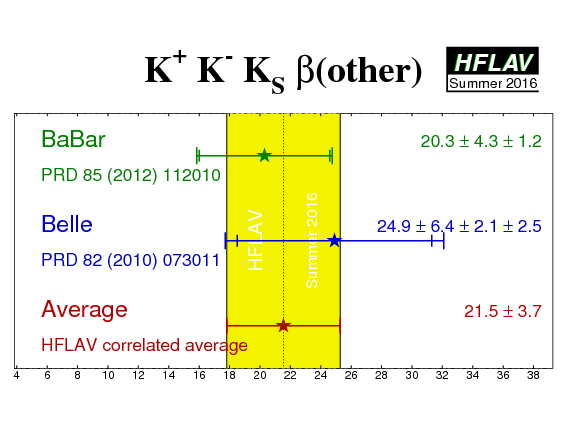
| Experiment | φKS | f0KS | other K+K−KS | Correlation | Reference | |||
|---|---|---|---|---|---|---|---|---|
| βeff ≡ φ1eff | ACP | βeff ≡ φ1eff | ACP | βeff ≡ φ1eff | ACP | |||
|
BaBar
(*)
N(BB)=470M |
(21 ± 6 ± 2)° | −0.05 ± 0.18 ± 0.05 | (18 ± 6 ± 4)° | −0.28 ± 0.24 ± 0.09 | (20.3 ± 4.3 ± 1.2)° | −0.02 ± 0.09 ± 0.03 | (stat) | PRD 85 (2012) 112010 |
|
Belle
(**)
N(BB)=657M |
(32.2 ± 9.0 ± 2.6 ± 1.4)° | 0.04 ± 0.20 ± 0.10 ± 0.02 | (31.3 ± 9.0 ± 3.4 ± 4.0)° | −0.30 ± 0.29 ± 0.11 ± 0.09 | (24.9 ± 6.4 ± 2.1 ± 2.5)° | −0.14 ± 0.11 ± 0.08 ± 0.03 | (stat) | PRD 82 (2010) 073011 |
| Average | (24 ± 5)° | −0.01 ± 0.14 | (22 ± 6)° | −0.29 ± 0.20 | (21.6 ± 3.7)° | −0.06 ± 0.08 | (stat) |
HFLAV correlated average
χ2 = 1.8/6 dof (CL=0.93 ⇒ 0.1σ) |
|
|

eps.gz png |

eps.gz png |

eps.gz png |
eps.gz png |
eps.gz png |

eps.gz png |
. | |
(*) The BaBar fit to K+K−KS finds a global minimum and four other local minima with -2 ln L values within 9 units of the global minimum (the closest is separated by 3.9 units). Values of the CP violation parameters are only quoted for the global minimum.
(**) The Belle fit to K+K−KS results in a four-fold ambiguity in the solution, all with consistent values of the CP parameters. The results quoted here correspond to solution 1 presented in the paper (which is preferred based on comparisons of the relative branching fractions of the scalar resonances to π+π− and K+K− to external measurements). The third source of uncertainty arises due to the composition of the Dalitz plot.
From the above results BaBar infer that the trigonometric reflection at π/2 - βeff is disfavoured at 4.8σ.
Time-dependent Dalitz plot analyses of B0 → π+π−KS have been performed by BaBar and Belle. As given above, parameters can be extracted in a form that allows a straightforward comparison/combination with those from time-dependent CP asymmetries in quasi-two-body b → qq-bar s modes. In addition, the effective weak phase βeff ≡ φ1eff is directly determined for two significant resonant contributions: f0KS and ρ0KS by both experiments. Both experiments find multiple solutions in the fits; in both cases we quote the results given as solution 1. BaBar also report parameters related to the intermediate states f2(1270)KS, fX(1300)KS, nonresonant π+π−KS and χc0KS (see b → cc-bar s modes above). A number of additional parameters, for example relating to the Q2B modes K*+π−, are also extracted, but are not tabulated here.
The third error in the results given below is due to Dalitz model uncertainty.
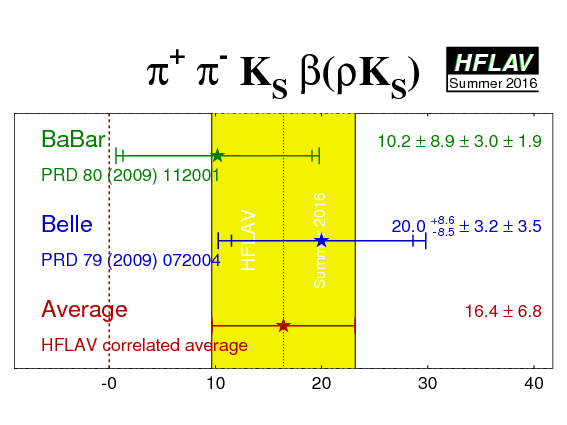
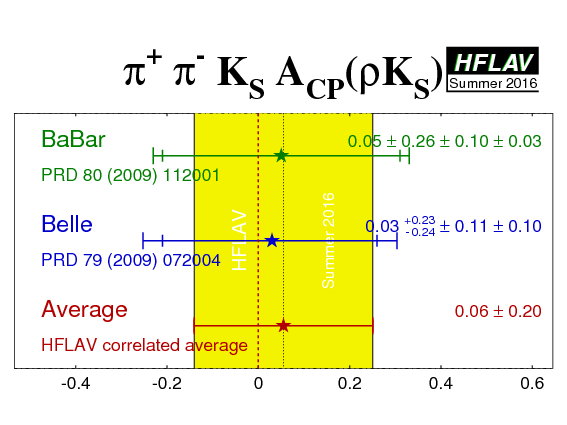
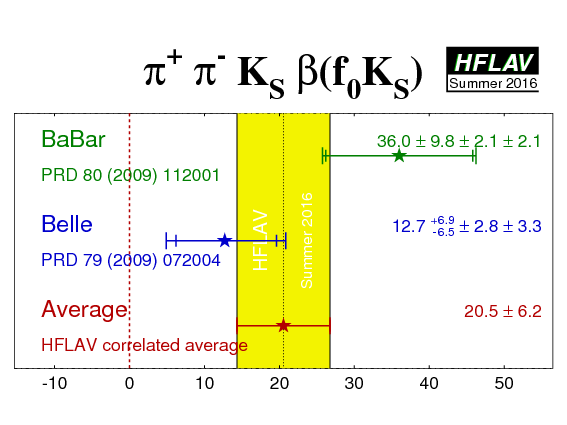
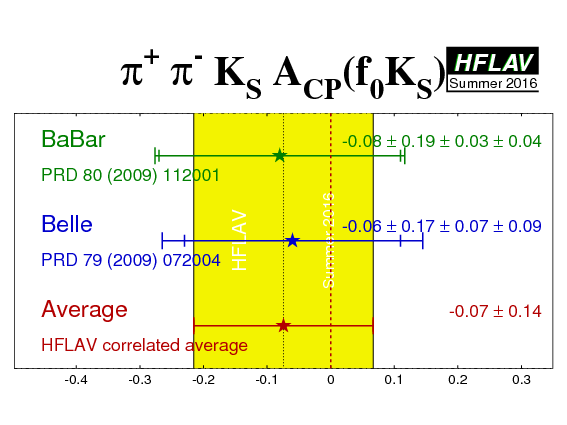
| Experiment | ρ0KS | f0KS | Correlation | Reference | ||
|---|---|---|---|---|---|---|
| βeff ≡ φ1eff | ACP | βeff ≡ φ1eff | ACP | |||
|
BaBar
(*)
N(BB)=383M |
(10.2 ± 8.9 ± 3.0 ± 1.9)° | 0.05 ± 0.26 ± 0.10 ± 0.03 | (36.0 ± 9.8 ± 2.1 ± 2.1)° | −0.08 ± 0.19 ± 0.03 ± 0.04 | (stat) | PRD 80 (2009) 112001 |
|
Belle
(*)
N(BB)=657M |
(20.0 +8.6 −8.5 ± 3.2 ± 3.5)° | 0.03 +0.23 −0.24 ± 0.11 ± 0.10 | (12.7 +6.9 −6.5 ± 2.8 ± 3.3)° | −0.06 ± 0.17 ± 0.07 ± 0.09 | (stat) | PRD 79 (2009) 072004 |
| Average | (16.4 ± 6.8)° | 0.06 ± 0.20 | (20.6 ± 6.2)° | −0.07 ± 0.14 | (stat) |
HFLAV correlated average
χ2 = 4.1/4 dof (CL=0.39 ⇒ 0.9σ) |
|
|
eps.gz png |
eps.gz png |
eps.gz png |
eps.gz png |
. | |
| Experiment | f2KS | fXKS | Nonresonant | χc0KS | Correlation | Reference | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| βeff ≡ φ1eff | ACP | βeff ≡ φ1eff | ACP | βeff ≡ φ1eff | ACP | βeff ≡ φ1eff | ACP | |||
|
BaBar
(*)
N(BB)=383M |
(14.9 ± 17.9 ± 3.1 ± 5.2)° | −0.28 +0.40 −0.35 ± 0.08 ± 0.07 | (5.8 ± 15.2 ± 2.2 ± 2.3)° | −0.13 +0.35 −0.33 ± 0.04 ± 0.09 | (0.4 ± 8.8 ± 1.9 ± 3.8)° | −0.01 ± 0.25 ± 0.06 ± 0.05 | (23.2 ± 22.4 ± 2.3 ± 4.2)° | 0.29 +0.44 −0.53 ± 0.03 ± 0.05 | (stat) | PRD 80 (2009) 112001 |
(*) Both experiments suffer from ambiguities in the solutions. The results quoted here correspond to solution 1 presented in the papers.
Since parameters related to the B0 → f0KS decay are obtained in both B0 → K+K−K0 and B0 → π+π−KS, we show compilations and naïve (uncorrelated) averages below.
|
Naïve (uncorrelated) averages for f0KS parameters |

eps.gz png |
eps.gz png |
. | |
The final state in the decay B → φ KS π0 is a mixture of CP-even and CP-odd amplitudes. However, since only φ K*0 resonant states contribute (in particular, φ K*0(892), φ K*00(1430) and φ K*02(1430) are seen), the composition can be determined from the analysis of B → φ K+ π−, assuming only that the ratio of branching fractions B(K*0 → KS π0)/B(K*0 → K+ π−) is the same for each exited kaon state.
BaBar have performed a simultaneous analysis of B → φ KS π0 and B → φ K+ π− that is time-dependent for the former mode and time-integrated for the latter. Such an analysis allows, in principle, all parameters of the B → φ K*0 system to be determined, including mixing-induced CP violation effects. The latter is determined to be Δφ00 = 0.28 ± 0.42 ± 0.04, where Δφ00 is half the weak phase difference between B0 and B0-bar decays to φK*00(1430). As presented above, this can also be presented in terms of the quasi-two-body parameter sin(2βeff00) = sin(2β+2Δφ00) = 0.97 +0.03−0.52. The highly asymmetric uncertainty arises due to the conversion from the phase to the sine of the phase, and the proximity of the physical boundary.
Similar sin(2βeff) parameters can be defined for each of the helicity amplitudes for both φ K*0(892) and φ K*02(1430). However, the relative phases between these decays are constrained due to the nature of the simultaneous analysis of B → φ KS π0 and B → φ K+ π−, and therefore these measurements are highly correlated. Instead of quoting all these results, BaBar provide an illustration of their measurements with the following differences:
where the first subscript indicates the helicity amplitude and the second indicates the spin of the kaon resonance. For the complete definitions of the Δδ and Δφ parameters, please refer to the BaBar paper.
Direct CP violation parameters for each of the contributing helicity amplitudes can also be measured. Again, these are determined from a simultaneous fit of B → φ KS π0 and B → φ K+ π−, with the precision being dominated by the statistics of the latter mode. The direct CP violation measurements are tabulated by HFLAV - Rare Decays.
The decay Bs → K+K− involves a b → uu-bar s transition, and hence has both penguin and tree contributions. Both mixing-induced and direct CP violation effects may arise, and additional input is needed to disentangle the contributions and determine γ and βseff. For example, the observables in Bd → π+π− can be related using U-spin, as proposed by Fleischer.
The observables are SCP, CCP, and AΔΓ. The alternative notations Amix = SCP and Adir = −CCP are sometimes found in the literature. All three observables can be treated as free parameters, but they are physically constrained to satisfy SCP2 + CCP2 + AΔΓ2 = 1. Note that the untagged decay distribution, from which an "effective lifetime" can be measured, retains sensitivity to AΔΓ. Averages of effective lifetimes are performed by the HFLAV lifetimes and oscillation group.
The observables have been measured by LHCb, who treat SCP, CCP, and AΔΓ as independent parameters.
| Experiment | SCP | CCP | AΔΓCP | Correlation | Reference |
|---|---|---|---|---|---|
|
LHCb Run 1
∫Ldt=3.0 fb−1 |
0.18 ± 0.06 ± 0.02 | 0.20 ± 0.06 ± 0.02 | −0.79 ± 0.07 ± 0.10 | (stat) | PR D98 (2018) 032004 |
|
LHCb Run 2
∫Ldt=1.9 fb−1 |
0.12 ± 0.03 ± 0.01 | 0.16 ± 0.03 ± 0.01 | −0.83 ± 0.05 ± 0.09 | (stat) (syst) | JHEP 2103 (2021) 075 |
| LHCb Average | 0.14 ± 0.03 | 0.17 ± 0.03 | −0.90 ± 0.09 (*) | (stat) | JHEP 2103 (2021) 075 |
(*) In JHEP 2103 (2021) 075 the results of the Run 1 analysis are updated to account for improved knowledge of Γs and ΔΓs. The central value of AΔΓCP changes to −0.97 ± 0.07, which is expected due to a shift in Γs with which it is strongly correlated. The combination of Run 1 and Run 2 results uses the updated values as inputs.
The decay Bs → φφ involves a b → ss-bar s transition, and hence is a "pure penguin" mode. Since the mixing phase and the decay phase are expected to cancel in the Standard Model, the prediction for the phase from the interference of mixing and decay is predicted to be φs(φφ) = 0 with low uncertainty. Due to the vector-vector nature of the final state, angular analysis is needed to separate the CP-even and CP-odd contributions. Such an analysis also makes it possible to fit directly for φs(φφ).
A constraint on φs(φφ) has been obtained by LHCb using their combined LHCb Run 1 and Run 2 data sample, corresponding to ∫Ldt=9.0 fb−1 (PRL 131 (2023) 171802), who measure φs(φφ) = −0.074 ± 0.069 and |λ| = 1.009 ± 0.030, where the statistical uncertainty is dominant. Results quoted with separated statistical and systematic uncertainties are available in the Run 1 and Run 2 publications.
The decay Bs → K*0K*0 involves a b → dd-bar s transition, and similarly is a "pure penguin" mode. In this case the possibility of SM contributions with a different weak phase to the penguin amplitude makes the theoretical prediction less straightforward. A U-spin analysis with the B0 decay mode to the same final state can, however, be used to make clean SM tests (see, e.g. hep-ph/0703137 and arXiv:0705.0477).
A significant complication arises due to the width of the K*(892)0 meson. This has been addressed by LHCb, through a full analysis of the Bs → (K+π−)(K−π+) decay, using a Kπ mass window from 750 to 1600 MeV/c2. In addition to the vector K*(892) resonance, contributions from Kπ S-wave and from the tensor K2*(1430) state are included. Assuming all amplitudes have contibutions only from the same weak phase, a value of φs((K+π−)(K−π+)) = −0.10 ± 0.13 (stat) ± 0.14 (syst) rad is measured, from a data sample of ∫Ldt=3.0 fb−1 (JHEP 1803 (2018) 140).
The b → qq-bar d penguin transitions are suppressed in the Standard Model, leading to small numbers of events available in these final states. If the top quark dominates in the loop, the phase in the decay amplitude (β ≡ φ1) cancels that in the B0–B0-bar mixing, so that S = C = 0. However, even within the Standard Model, there may be non-negligible contributions with u or c quarks in the penguin loop (or from rescattering, etc.) so that different values of S and C are possible. In this case, these can be used to obtain constraints on γ ≡ φ3, and hence test if any non-Standard Model contributions are present.
At present we do not apply a rescaling of the results to a common, updated set of input parameters.
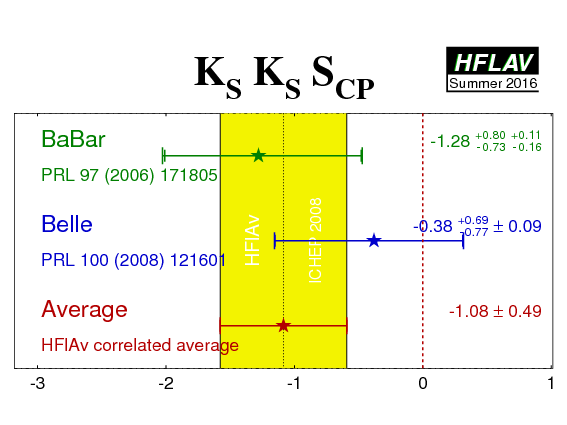
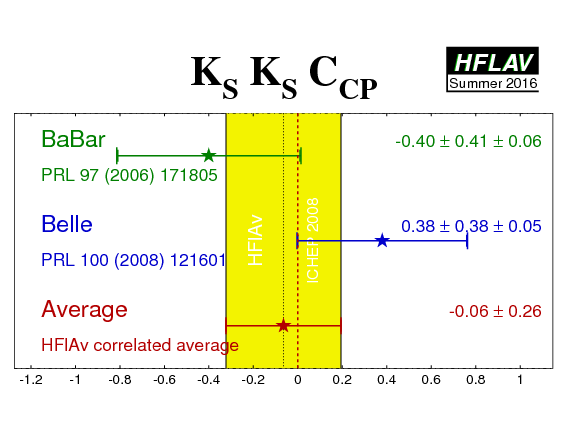
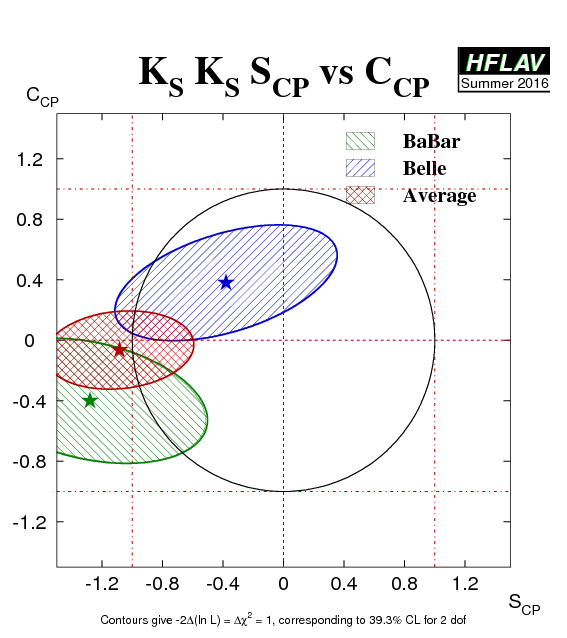
| Experiment | SCP (KSKS) | CCP (KSKS) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=350M |
−1.28 +0.80 −0.73 +0.11 −0.16 | −0.40 ± 0.41 ± 0.06 | −0.32 (stat) | PRL 97 (2006) 171805 |
|
Belle
N(BB)=657M |
−0.38 +0.69 −0.77 ± 0.09 | 0.38 ± 0.38 ± 0.05 | 0.48 (stat) | PRL 100 (2008) 121601 |
| Average | −1.08 ± 0.49 | −0.06 ± 0.26 | 0.14 |
HFLAV correlated average
χ2 = 2.5/2 dof (CL=0.29 ⇒ 1.1σ) |
|
|
eps.gz png |
eps.gz png |
eps.gz png |
|
(*) Note that the BaBar result is outside of the physical region, as is the average. The interpretation of the results given above has to be done with the greatest care.
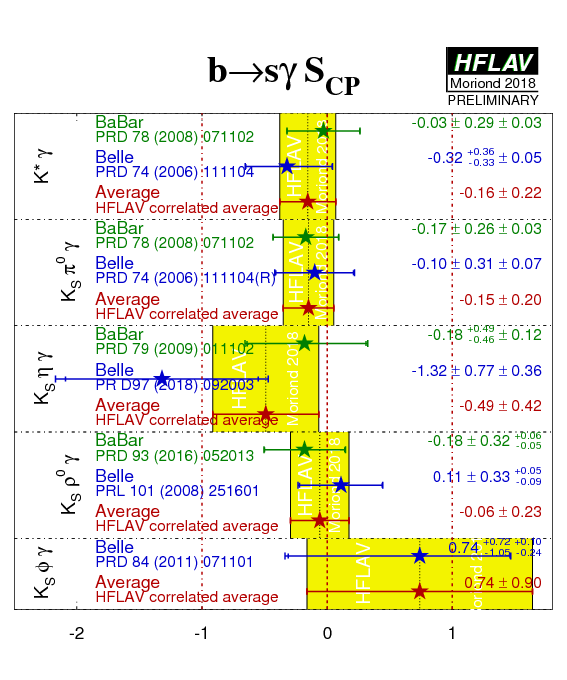
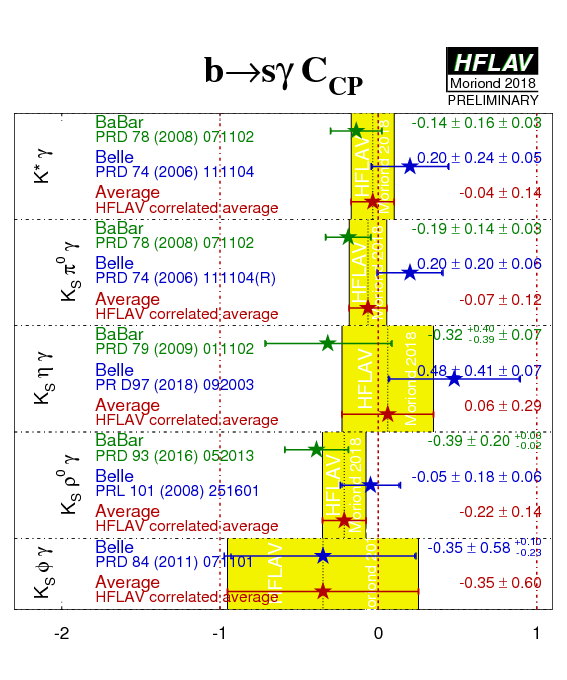
Time-dependent analyses of radiative b decays such as B0→ KSπ0γ, probe the polarization of the photon. In the SM, the photon helicity is dominantly left-handed for b → sγ, and right-handed for the conjugate process. As a consequence, B0 → KSπ0γ behaves like an effective flavor eigenstate, and mixing-induced CP violation is expected to be small - a simple estimation gives: S ~ −2(ms/mb)sin(2β) ≡ −2(ms/mb)sin(2φ1) (with an assumption that the Standard Model dipole operator is dominant). Corrections to the above may allow values of S as large as 10% in the SM.
Atwood et al. have shown that (with the same assumption) an inclusive analysis with respect to KSπ0 can be performed, since the properties of the decay amplitudes are independent of the angular momentum of the KSπ0 system. However, if non-dipole operators contribute significantly to the amplitudes, then the Standard Model mixing-induced CP violation could be larger than the expectation given above, and the CPV parameters may vary slightly over the KSπ0γ Dalitz plot, for example as a function of the KSπ0 invariant mass.
An inclusive KSπ0γ analysis has been performed by Belle using the invariant mass range up to 1.8 GeV/c2. Belle also gives results for the K*(892) region: 0.8 GeV/c2 to 1.0 GeV/c2. BaBar has measured the CP-violating asymmetries separately within and outside the K*(892) mass range: 0.8 GeV/c2 to 1.0 GeV/c2 is again used for K*(892)γ candidates, while events with invariant masses in the range 1.1 GeV/c2 to 1.8 GeV/c2 are used in the "KSπ0γ (not K*(892)γ)" analysis.
We quote two averages: one for K*(892) only, and the other one for the inclusive KSπ0γ decay (including the K*(892)). If the Standard Model dipole operator is dominant, both should give the same quantities (the latter naturally with smaller statistical error). If not, care needs to be taken in interpretation of the inclusive parameters; while the results on the K*(892) resonance remain relatively clean.
In addition to results with the KSπ0γ final state, both BaBar and Belle have results using KSηγ and KSρ0γ (see footnotes below table), while Belle also has results using KSφγ.
At present we do not apply a rescaling of the results to a common, updated set of input parameters.
| Mode | Experiment | SCP (b → sγ) | CCP (b → sγ) | Correlation | Reference | ||||
|---|---|---|---|---|---|---|---|---|---|
| K*(892)γ |
BaBar
N(BB)=467M |
−0.03 ± 0.29 ± 0.03 | −0.14 ± 0.16 ± 0.03 | 0.05 (stat) | PRD 78 (2008) 071102 | ||||
|
Belle
N(BB)=535M |
−0.32 +0.36 −0.33 ± 0.05 | 0.20 ± 0.24 ± 0.05 | 0.08 (stat) | PRD 74 (2006) 111104 | |||||
| Average | −0.16 ± 0.22 | −0.04 ± 0.14 | 0.06 |
HFLAV correlated average
χ2 = 1.9/2 dof (CL=0.40 ⇒ 0.9σ) |
|||||
|
KSπ0γ
(incl. K*γ) |
BaBar
N(BB)=467M |
−0.17 ± 0.26 ± 0.03 | −0.19 ± 0.14 ± 0.03 | 0.04 (stat) | PRD 78 (2008) 071102 | ||||
|
Belle
N(BB)=535M |
−0.10 ± 0.31 ± 0.07 | 0.20 ± 0.20 ± 0.06 | 0.08 (stat) | PRD 74 (2006) 111104(R) | |||||
| Average | −0.15 ± 0.20 | −0.07 ± 0.12 | 0.05 |
HFLAV correlated average
χ2 = 2.4/2 dof (CL=0.30 ⇒ 1.0σ) |
|||||
| KS η γ |
BaBar
N(BB)=465M |
−0.18 +0.49 −0.46 ± 0.12 | −0.32 +0.40 −0.39 ± 0.07 | −0.17 (stat) | PRD 79 (2009) 011102 | ||||
|
Belle
N(BB)=772M |
−1.32 ± 0.77 ± 0.36 | 0.48 ± 0.41 ± 0.07 | −0.15 (stat) | PR D97 (2018) 092003 | |||||
| Average | −0.49 ± 0.42 | 0.06 ± 0.29 | −0.15 |
HFLAV correlated average
χ2 = 2.9/2 dof (CL=0.24 ⇒ 1.2σ) |
|||||
| KS ρ0 γ (*) |
BaBar
N(BB)=471M |
−0.18 ± 0.32 +0.06 −0.05 | −0.39 ± 0.20 +0.03 −0.02 | −0.09 (stat) | PRD 93 (2016) 052013 | ||||
|
Belle
N(BB)=657M |
0.11 ± 0.33 +0.05 −0.09 | −0.05 ± 0.18 ± 0.06 | 0.04 (stat) | PRL 101 (2008) 251601 | |||||
| Average(*) | −0.06 ± 0.23 | −0.22 ± 0.14 | −0.02 |
HFLAV correlated average
χ2 = 1.9/2 dof (CL=0.38 ⇒ 0.9σ) |
|||||
| KS φ γ |
Belle
N(BB)=772M |
0.74 +0.72 −1.05 +0.10 −0.24 | −0.35 ± 0.58 +0.10 −0.23 | - | PRD 84 (2011) 071101 | ||||
|
|
eps.gz png |
eps.gz png |
|
||||||
(*) Due to the non-negligible width of the ρ0 meson, decays selected as B0 → KSρ0γ can include a significant contribution from K*+−π−+γ decays, which are flavour-specific and do not have the same oscillation phenomenology. Both BaBar and Belle measure Seff for all B decay candidates with the ρ0 selection being 0.6 < m(π+π−) < 0.9 GeV/c2, obtaining 0.14 ± 0.25 ±0.03 (BaBar) and 0.09 ± 0.27 +0.04−0.07 (Belle). These values are then corrected for a "dilution factor", that is evaluated with different methods in the two experiments: BaBar obtain −0.78 +0.19−0.17 while Belle obtain 0.83 +0.19−0.03. Until the discrepancy between these values is understood, the average of the results should be treated with extreme caution.
A similar analysis can be performed for radiative Bs decays to, for example, the φγ final state. As for other observables determined with self-conjugate final states produced in Bs decays the effective lifetime, or equivalently the AΔΓ parameter, also provides sensitivity. The LHCb collaboration has determined the relevant parameters in Bs → φγ decays.
| Mode | Experiment | SCP (b → sγ) | CCP (b → sγ) | AΔΓ (b → sγ) | Correlation | Reference |
|---|---|---|---|---|---|---|
| Bs → φγ |
LHCb
∫Ldt=3.0 fb−1 |
0.43 ± 0.30 ± 0.11 | 0.11 ± 0.29 ± 0.11 | −0.67 +0.37−0.41 ± 0.17 | (stat) | PRL 123 (2019) 081802 |
Similar to the b → sγ transitions discussed above, time-dependent analyses of radiative b decays such as B0→ ρ0γ probe the polarization of the photon emitted in radiative b → dγ decays. However, since the CP violating phase from the b → d decay amplitude cancels that from the Bd–Bd-bar mixing (to an approximation that is exact in the limit of top quark dominance in the loops), the asymmetry is suppressed even further in the Standard Model. An observable signal would be a sign of a new physics amplitude emitting right-handed photons and carrying a new CP violating phase.
A time-dependent analysis of the B0→ ρ0γ channel has been carried out by Belle.
At present we do not apply a rescaling of the results to a common, updated set of input parameters.
| Mode | Experiment | SCP (b → dγ) | CCP (b → dγ) | Correlation | Reference |
|---|---|---|---|---|---|
| ρ0γ |
Belle
N(BB)=657M |
−0.83 ± 0.65 ± 0.18 | 0.44 ± 0.49 ± 0.14 | −0.08 (stat) | PRL 100 (2008) 021602 |
The observables have been measured by BaBar, Belle & LHCb. Note that at the B factories the observables are in principle uncorrelated (due to the fact that the time variable, Δt, has the range −∞ < Δt < +∞ – small correlations can be induced e.g.by backgrounds), at hadron colliders a non-zero correlation is expected (the time variable t takes the range 0 < t < +∞). Please note that at present we do not apply a rescaling of the results to a common, updated set of input parameters. Correlation due to common systematics are neglected in the following averages.
| Experiment | SCP (π+π−) | CCP (π+π−) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=467M |
−0.68 ± 0.10 ± 0.03 | −0.25 ± 0.08 ± 0.02 | −0.06 (stat) | PRD 87 (2013) 052009 |
|
Belle
N(BB)=772M |
−0.64 ± 0.08 ± 0.03 | −0.33 ± 0.06 ± 0.03 | −0.10 (stat) | PRD 88 (2013) 092003 |
|
LHCb Run 1
∫Ldt=3.0 fb−1 |
−0.63 ± 0.05 ± 0.01 | −0.34 ± 0.06 ± 0.01 | 0.45 (stat) | PR D98 (2018) 032004 |
|
LHCb Run 2
∫Ldt=1.9 fb−1 |
−0.706 ± 0.042 ± 0.013 | −0.311 ± 0.045 ± 0.015 | 0.394 (stat) 0.306 (syst) | JHEP 2103 (2021) 075 |
| LHCb Average | −0.672 ± 0.034 | −0.320 ± 0.038 | 0.405 (stat) | JHEP 2103 (2021) 075 |
| Average | −0.666 ± 0.029 | −0.311 ± 0.030 | 0.288 |
HFLAV correlated average
χ2 = 0.8/4 dof (CL=0.94 ⇒ 0.1σ) |
|
|

eps.gz png |

eps.gz png |
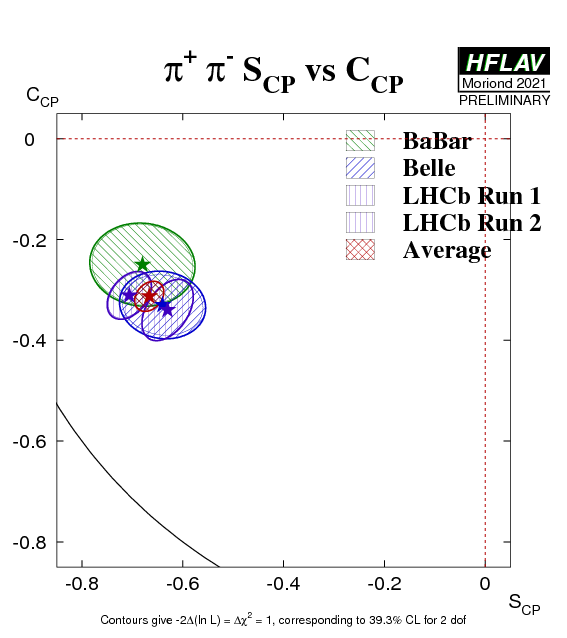
eps.gz png |
|
Interpretations:
The
Gronau-London
isospin analysis allows a constraint on α ≡ φ2
to be extracted from the ππ system even in the presence of non-negligible
penguin contributions.
The isospin analysis uses as input the branching fractions and
CP-violating charge asymmetries of all three ππ decay modes
(π+π−,
π−π0,
π0π0).
(Constraints on α ≡ φ2 can be obtained without information on S(π0π0), which has not yet been measured.)
See our combination of results to obtain constraints on α ≡ φ2.
Both Belle and
BaBar
give confidence level interpretations for α ≡ φ2.
Belle
exclude the range 9.5° < φ2 < 81.6° at 68% confidence level.
BaBar
state that the true value lies in the range 71° < α < 109° at the 68% confidence level (considering the solution consistent with the Standard Model).
NB. It is implied in the above constraints on α ≡ φ2 that a mirror solution at α → α + π ≡ φ2 → φ2 + π also exists.
For more details on the world average for α ≡ φ2, calculated with different statistical treatments, refer to the CKMfitter and UTfit pages.
Both BaBar and Belle have performed a full time-dependent Dalitz plot analyses of the decay Bd → (ρπ)0 → π+π−π0, which allows to simultaneously determine the complex decay amplitudes and the CP-violating weak phase α ≡ φ2. The analysis follows the idea of Snyder and Quinn (1993), implemented as suggested by Quinn and Silva. The experiments determine 27 coefficients of the form factor bilinears from the fit to data. Physics parameters, such as the quasi-two-body parameters, and the phases δ+−=arg[A−+A+−*] and the UT angle α ≡ φ2, are determined from subsequent fits to the bilinear coefficients.
Please note that at present we do not apply a rescaling of the results to a common, updated set of input parameters. Correlation due to common systematics are neglected in the following averages.
| [The table of averages of the form factor bilinears is suppressed here for the benefit of the nonspecialist. Those interested in the details can find them here.] |
|
Compilation of averages of the form factor bilinears.
The data in these plots is taken from (BaBar) PRD 88 (2013) 012003 and (Belle) PRL 98 (2007) 221602. |

eps.gz png |
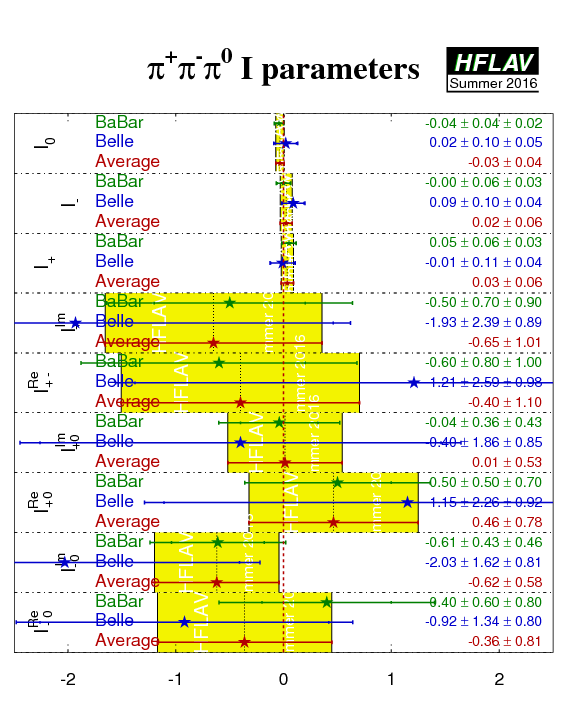
eps.gz png |
From the bilinear coefficients given above, both experiments extract "quasi-two-body" (Q2B) parameters. Considering only the charged ρ bands in the Dalitz plot, the Q2B analysis involves 5 different parameters, one of which − the charge asymmetry ACP(ρπ) − is time-independent. The time-dependent decay rate is given by
where Qtag=+1(−1) when the tagging meson is a B0 (B0-bar). CP symmetry is violated if either one of the following conditions is true: ACP(ρπ)≠0, Cρπ≠0 or Sρπ≠0. The first two correspond to CP violation in the decay, while the last condition is CP violation in the interference of decay amplitudes with and without Bd mixing.
We average the quasi-two-body parameters provided by the experiments, which should be equivalent to determining average values directly from the averaged bilinear coefficients.
It can be convenient to transform the experimentally motivated
CP parameters ACP(ρπ) and Cρπ
into the physically motivated choices
A+−(ρπ) =
(|κ+−|2−1)/(|κ+−|2+1) =
−(ACP(ρπ)+Cρπ+ACP(ρπ)ΔCρπ)/(1+ΔCρπ + ACP(ρπ)Cρπ),
A−+(ρπ) =
(|κ−+|2−1)/(|κ−+|2+1) =
(−ACP(ρπ)+Cρπ+ACP(ρπ)ΔCρπ)/(−1+ΔCρπ + ACP(ρπ)Cρπ),
where
κ+− = (q/p)Abar−+/A+− and
κ−+ = (q/p)Abar+−/A−+.
With this definition A−+(ρπ) (A+−(ρπ))
describes CP violation in Bd decays
where the ρ is emitted (not emitted) by the spectator interaction.
Both experiments obtain values for A+− and A−+,
which we average.
Again, this procedure should be equivalent to extracting these values
directly from the previous results.
In addition to the Bd→ ρ+−π−+ quasi-two-body contributions to the π+π−π0 final state, there can also be a Bd→ ρ0π0 component. Both experiments have also extracted the quasi-two-body parameters associated with this intermediate state.
Note again that at present we do not apply a rescaling of the results to a common, updated set of input parameters. Correlations due to possible common systematics are neglected in the following averages.
The citation given for Belle in the tables below corresponds to a short article published in PRL. A more detailed article on the same analysis is also available as PRD 77 (2008) 072001.
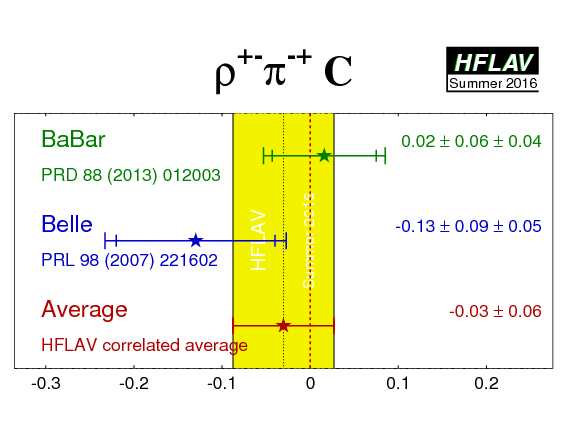
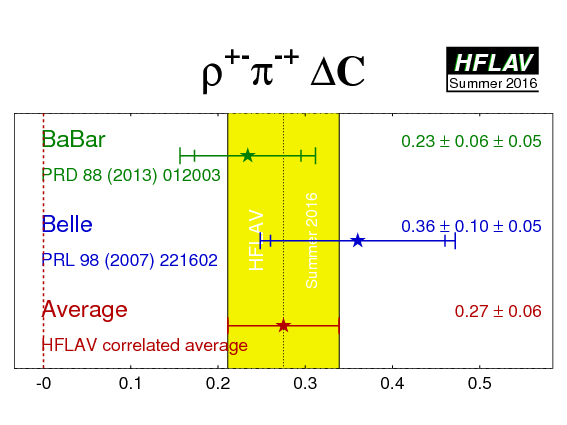
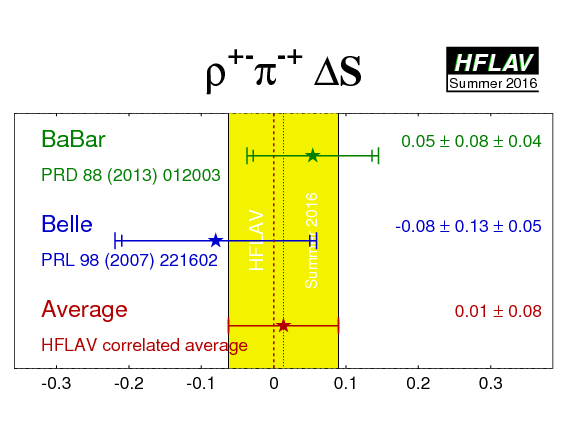
| Experiment | ACP (ρ+−π−+) | C (ρ+−π−+) | S (ρ+−π−+) | ΔC (ρ+−π−+) | ΔS (ρ+−π−+) | Correlations | Reference |
|---|---|---|---|---|---|---|---|
|
BaBar
N(BB)=471M |
−0.10 ± 0.03 ± 0.02 | 0.02 ± 0.06 ± 0.04 | 0.05 ± 0.08 ± 0.03 | 0.23 ± 0.06 ± 0.05 | 0.05 ± 0.08 ± 0.04 | (stat) | PRD 88 (2013) 012003 |
|
Belle
N(BB)=449M |
−0.12 ± 0.05 ± 0.04 | −0.13 ± 0.09 ± 0.05 | 0.06 ± 0.13 ± 0.05 | 0.36 ± 0.10 ± 0.05 | −0.08 ± 0.13 ± 0.05 | (stat) | PRL 98 (2007) 221602 |
| Average | −0.11 ± 0.03 | −0.03 ± 0.06 | 0.06 ± 0.07 | 0.27 ± 0.06 | 0.01 ± 0.08 | (stat) |
HFLAV correlated average
χ2 = 3.5/5 dof (CL=0.63 ⇒ 0.5σ) |
|
|

eps.gz png |
eps.gz png |

eps.gz png |
eps.gz png |
eps.gz png |
. | |
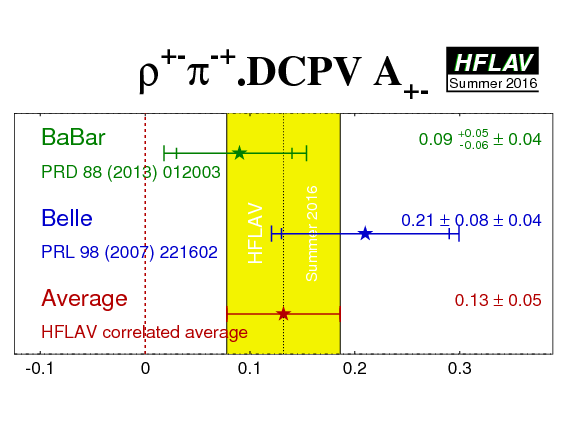
| Experiment | A−+ (ρ+−π−+) | A+− (ρ+−π−+) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=471M |
−0.12 ± 0.08 +0.04 −0.05 | 0.09 +0.05 −0.06 ± 0.04 | 0.55 | PRD 88 (2013) 012003 |
|
Belle
N(BB)=449M |
0.08 ± 0.16 ± 0.11 | 0.21 ± 0.08 ± 0.04 | 0.47 | PRL 98 (2007) 221602 |
| Average | −0.08 ± 0.08 | 0.13 ± 0.05 | 0.37 |
HFLAV correlated average
χ2 = 1.5/2 dof (CL=0.47 ⇒ 0.7σ) |
|
|

eps.gz png |
eps.gz png |
eps.gz png |
|
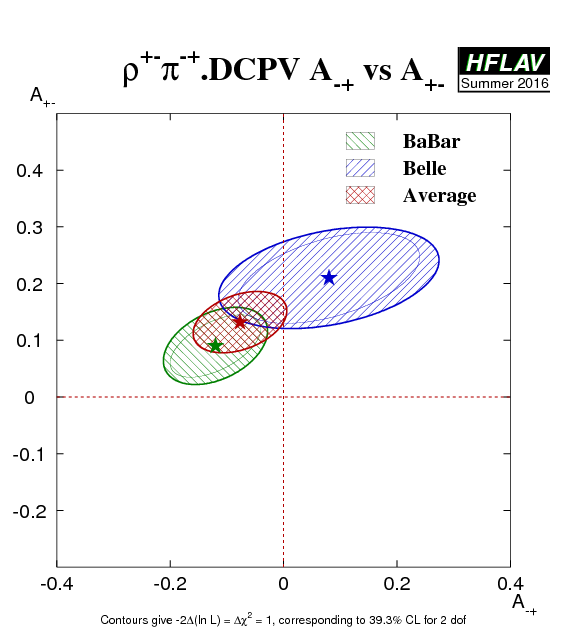
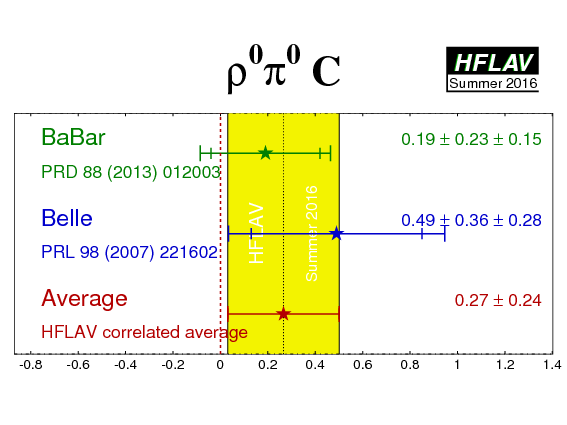
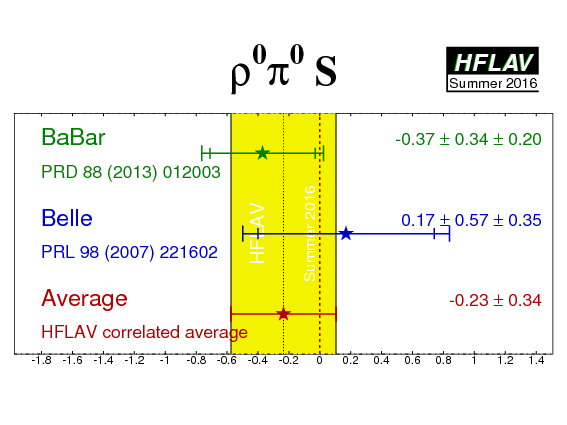
| Experiment | C (ρ0π0) | S (ρ0π0) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=471M |
0.19 ± 0.23 ± 0.15 | −0.37 ± 0.34 ± 0.20 | 0.00 | PRD 88 (2013) 012003 |
|
Belle
N(BB)=449M |
0.49 ± 0.36 ± 0.28 | 0.17 ± 0.57 ± 0.35 | 0.08 | PRL 98 (2007) 221602 |
| Average | 0.27 ± 0.24 | −0.23 ± 0.34 | 0.02 |
HFLAV correlated average
χ2 = 0.8/2 dof (CL=0.68 ⇒ 0.4σ) |
|
|
eps.gz png |
eps.gz png |

eps.gz png |
|
Interpretations:
The information given above can be used to extract α ≡ φ2.
A confidence level interpretation for α can be obtained by scanning over the measured form factor bilinears.
In addition, information from the B → ρπ SU(2) partners can be included via an isospin pentagon relation.
The isospin analysis uses as input the branching fractions and
CP-violating charge asymmetries of all five ρπ decay modes
(ρ+π−,ρ−π+,
ρ0π0, ρ+π0,
ρ0π+).
With all information in the ρπ channels put together,
Belle
obtain the constraint 68° < φ2 < 95° at 68% confidence level,
for the solution consistent with the Standard Model.
BaBar
present a scan, but not an interval, for α, since their studies indicate that the scan is not statistically robust and cannot be interpreted as 1-CL.
NB. It is implied in the above constraints on α ≡ φ2 that a mirror solution at α → α + π ≡ φ2 → φ2 + π also exists.
For more details on the world average for α ≡ φ2, calculated with different statistical treatments, refer to the CKMfitter and UTfit pages.
The vector particles in the pseudoscalar to vector-vector decay Bd → ρ+ρ− can have longitudinal and transverse relative polarization with different CP properties. The decay is found to be dominated by the longitudinally polarized component:
At present we do not apply a rescaling of the results to a
common, updated set of input parameters.
The CP parameters measured are those for the longitudinally polarized component
(ie. Sρρ,long, Cρρ,long).
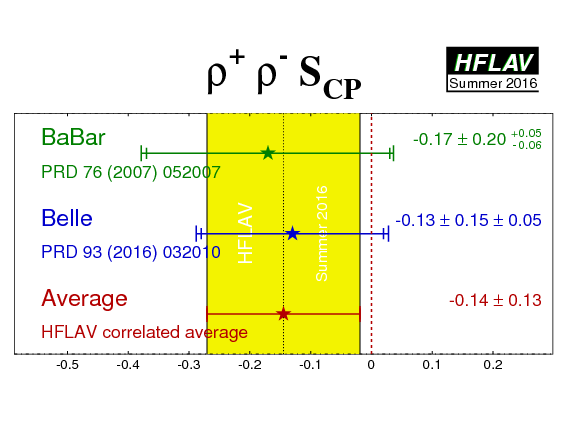
| Experiment | SCP (ρ+ρ−) | CCP (ρ+ρ−) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=387M |
−0.17 ± 0.20 +0.05 −0.06 | 0.01 ± 0.15 ± 0.06 | −0.04 (stat) | PRD 76 (2007) 052007 |
|
Belle
N(BB)=772M |
−0.13 ± 0.15 ± 0.05 | 0.00 ± 0.10 ± 0.06 | −0.02 (stat) | PRD 93 (2016) 032010 |
| Average | −0.14 ± 0.13 | 0.00 ± 0.09 | −0.02 |
HFLAV correlated average
χ2 = 0.03/2 dof (CL=0.99 ⇒ 0.02σ) |
|
|
eps.gz png |

eps.gz png |

eps.gz png |
|
Since the decay B0 → ρ0ρ0 results in an all charged particle final state, its time-dependent CP violation parameters can be determined experimentally, if difficulties related to the small branching fraction and large backgrounds can be overcome. BaBar measure the longitudinally polarized component to be
It should be noted that the Belle results for the ρ0ρ0 polarisation are in some tension with those from BaBar. Belle determine
There is also a measurement from LHCb of this quantity
At present we do not apply a rescaling of the results to a
common, updated set of input parameters.
The CP parameters measured are those for the longitudinally polarized component
(ie. Sρρ,long, Cρρ,long).
| Experiment | SCP (ρ0ρ0) | CCP (ρ0ρ0) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=465M |
0.3 ± 0.7 ± 0.2 | 0.2 ± 0.8 ± 0.3 | 0.0 (stat) | PRD 78 (2008) 071104(R) |
Interpretations:
The
Gronau-London
isospin analysis allows a constraint on α ≡ φ2
to be extracted from the ρρ system even in the presence of non-negligible
penguin contributions.
The isospin analysis uses as input the branching fractions and
CP-violating charge asymmetries of the longitudinal components of all three ρρ decay modes
(ρ+ρ−,
ρ−ρ0,
ρ0ρ0).
(A similar analysis could be done for each polarisation amplitude, but the others are found to not be statisticall significant.)
Constraints on α ≡ φ2 have been set by both BaBar and Belle. The most recent values are
NB. It is implied in the above constraints on α ≡ φ2 that a mirror solution at α → α + π ≡ φ2 → φ2 + π also exists.
For more details on the world average for α ≡ φ2, calculated with different statistical treatments, refer to the CKMfitter and UTfit pages.
Both BaBar and Belle collaborations have performed Q2B analyses of the Bd → a1+−π−+ decay, reconstructed in the final state π+π−π+π−.
| Experiment | ACP (a1+−π−+) | C (a1+−π−+) | S (a1+−π−+) | ΔC (a1+−π−+) | ΔS (a1+−π−+) | Correlations | Reference |
|---|---|---|---|---|---|---|---|
|
BaBar
N(BB)=384M |
−0.07 ± 0.07 ± 0.02 | −0.10 ± 0.15 ± 0.09 | 0.37 ± 0.21 ± 0.07 | 0.26 ± 0.15 ± 0.07 | −0.14 ± 0.21 ± 0.06 | (stat) | PRL 98 (2007) 181803 |
|
Belle
N(BB)=772M |
−0.06 ± 0.05 ± 0.07 | −0.01 ± 0.11 ± 0.09 | −0.51 ± 0.14 ± 0.08 | 0.54 ± 0.11 ± 0.07 | −0.09 ± 0.14 ± 0.06 | (stat) | PRD 86 (2012) 092012 |
| Average | −0.06 ± 0.06 | −0.05 ± 0.11 | −0.20 ± 0.13 | 0.43 ± 0.10 | −0.10 ± 0.12 | (stat) |
HFLAV correlated average
χ2 = 12/5 dof (CL=0.03 ⇒ 2.1σ) |
|
|
eps.gz png | eps.gz png | eps.gz png | eps.gz png | eps.gz png | . | |
| Experiment | A−+ (a1+−π−+) | A+− (a1+−π−+) | Correlation | Reference |
|---|---|---|---|---|
|
BaBar
N(BB)=384M |
0.07 ± 0.21 ± 0.15 | 0.15 ± 0.15 ± 0.07 | 0.63 (stat) | PRL 98 (2007) 181803 |
|
Belle
N(BB)=772M |
−0.04 ± 0.26 ± 0.19 | 0.07 ± 0.08 ± 0.10 | 0.61 (stat) | PRD 86 (2012) 092012 |
| Average | 0.02 ± 0.20 | 0.10 ± 0.10 | 0.38 |
HFLAV correlated average
χ2 = 0.2/2 dof (CL=0.92 ⇒ 0.1σ) |
|
|
eps.gz png | eps.gz png | eps.gz png | |
Interpretations:
The parameter αeff ≡ φ2,eff,
which reduces to α ≡ φ2 in the limit of
no penguin contributions, can be extracted from the above results.
BaBar obtain αeff = (78.6 ± 7.3)°. Belle obtain φ2,eff = (107.3 ± 6.6 (stat) ± 4.8 (syst))°.
NB. There is a four-fold ambiguity in the above results.
For more details on the world average for α ≡ φ2, calculated with different statistical treatments, refer to the CKMfitter and UTfit pages.
World averages for α ≡ φ2, combining all available measurements and calculated with different statistical treatments, have been calculated by the CKMfitter and UTfit groups. In addition, the BaBar and Belle collaborations have combined their results on B → ππ, πππ0 and ρρ to obtain
| α ≡ φ2 = (88 ± 5)° |
The above solution is that consistent with the Standard Model (an ambiguous solution shifted by 180° exists). The strongest constraint currently comes from the B → ρρ system. The inclusion of results from Bd → a1+−π−+ does not significantly affect the average.
Independently from the constraints on α ≡ φ2 obtained by the experiments or other groups, the results summarised above are statistically combined to produce world average constraints. The combination is performed with the GammaCombo framework and follows a frequentist procedure, similar to that described in detail in arXiv:1705.02981.
The input measurements used in the combination are those listed above for time-dependent CP violation parameters in Bd→ π+π−, π+π−π0 and ρ+ρ− and ρ0ρ0. Additional inputs for the branching fractions and (for ρρ) polarisation fractions, for these modes and for their isospin partners are taken from the HFLAV - Rare Decays subgroup. The CP asymmetry parameters for the isospin partner B+ decay modes are also taken from the HFLAV - Rare Decays subgroup, as is the corresponding parameter for Bd→ π0π0 mode, for which no time-dependent measurement is yet possible. The ratio of B+ to B0 lifetimes is taken from the HFLAV - Oscillations/Lifetime subgroup. Individual measurements are used as inputs, rather than the HFLAV averages, in order to facilitate cross-checks and to ensure the most appropriate treatment of correlations. A combination based on the HFLAV averages for each of the quantities measured by experiments gives consistent results.
The obtained world average for the Unitarity Triangle angle α ≡ φ2 is
The fit has a χ2 of 22.37 with 57 observables and 24 parameters. Using the χ2 distribution, this corresponds to a p-value of 92% (or 0.1σ). A coverage check with pseudoexperiments gives a p-value of (91.9 ± 0.3)%.
An ambiguous solution also exists at α ≡ φ2 ⇔ α + π ≡ φ2 + π.
The secondary minimum close to zero is disfavoured by physical arguments not included in the isospin analysis, as discussed in arXiv:1705.02981.
Figures:
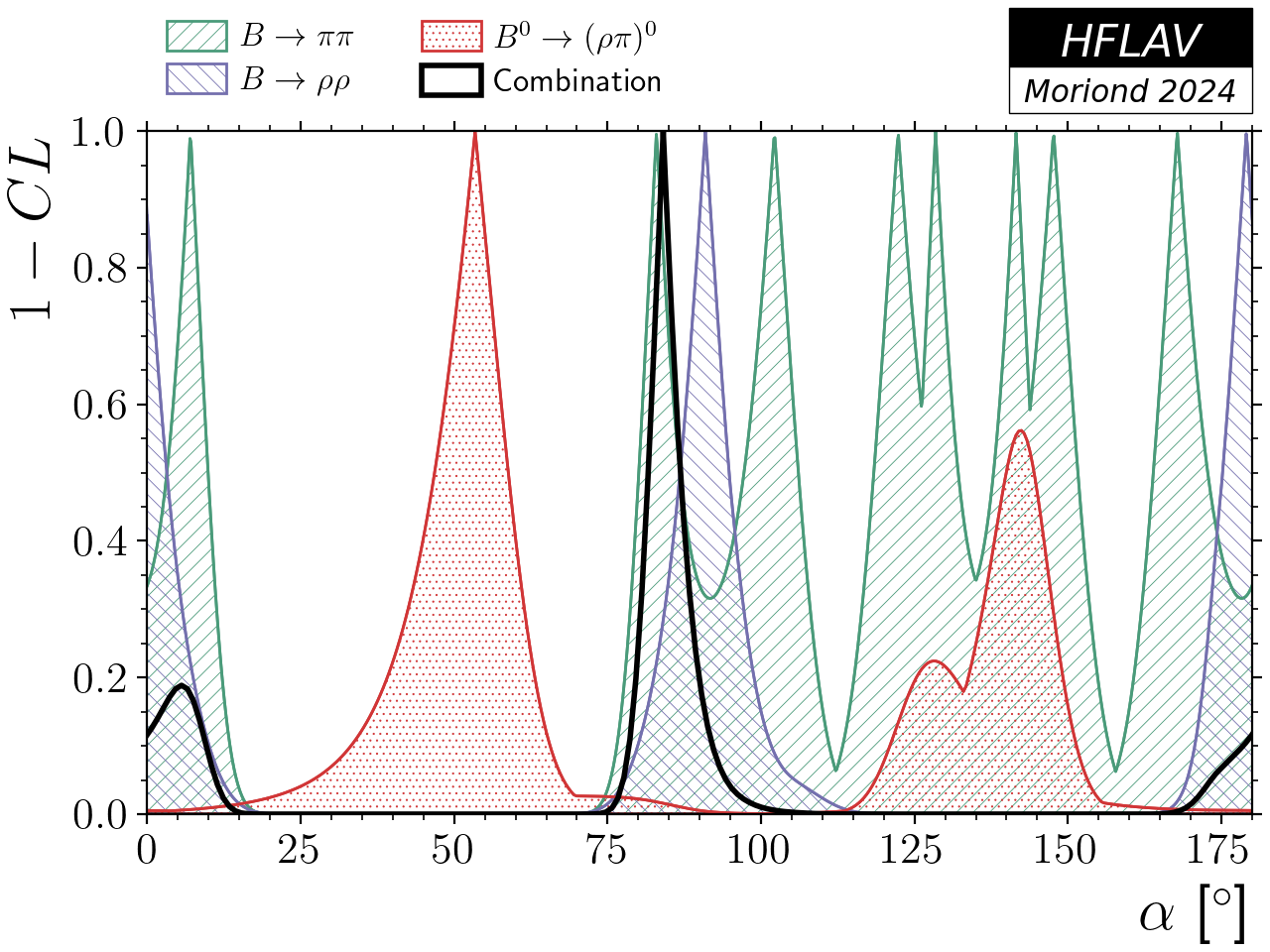
| World average of α ≡ φ2, in terms of 1−CL, split by decay mode. |

pdf png |
|
Neutral B meson decays such as Bd → D+−π−+, Bd → D*+−π−+ and Bd → D+−ρ−+ provide sensitivity to γ ≡ φ3 because of the interference between the Cabibbo-favoured amplitude (e.g. B0 → D−π+) with the doubly Cabibbo-suppressed amplitude (e.g. B0 → D+π−). The relative weak phase between these two amplitudes is −γ ≡ −φ3 and, when combined with the BdBd mixing phase, the total phase difference is −(2β+γ) ≡ −(2φ1+φ3).
The size of the CP violating effect in each mode depends on the ratio of magnitudes of the suppressed and favoured amplitudes, e.g., rDπ = |A(B0 → D+π−)/A(B0 → D−π+)|, as well as the strong phase between the amplitudes, usually denoted e.g. δDπ. Each of the ratios rDπ, rD*π and rDρ is expected to be about 0.02, and can be obtained experimentally from the corresponding suppressed charged B decays, (e.g., B+ → D+π0) using isospin, or from self-tagging decays with strangeness (e.g., B0 → Ds+π−), using SU(3). In the latter case, the theoretical uncertainties are hard to quantify. The smallness of the r values makes direct extractions from, e.g., the D+−π−+ system very difficult. There are different conventions in use for the definition of the strong phase difference, which can make a comparison of results in terms of this parameter non-trivial.
Both BaBar and Belle exploit partial reconstructions of D*+−π−+ to increase the available statistics. Both experiments also reconstruct D+−π−+ and D*+−π−+ fully, and BaBar includes the mode D+−ρ−+. LHCb have also performed the analysis with fully reconstructed D+−π−+ decays. Additional states with similar quark content are also possible, but for vector-vector final states an angular analysis is required, while states containing higher resonances may suffer from uncertainties due to nonresonant or other contributions.
BaBar, Belle and LHCb use different observables:
Here we convert the Belle and LHCb results to express them in terms of a and c. Correlations are taken into account in the LHCb case, where significant correlations are reported. Explicitly, the conversion reads: a = −(S+ + S−)/2, c = −(S+ − S−)/2
At present we do not rescale the results to a common set of input parameters. Also, common systematic errors are not considered.
| Mode | Experiment | a | c | Correlation | Reference |
|---|---|---|---|---|---|
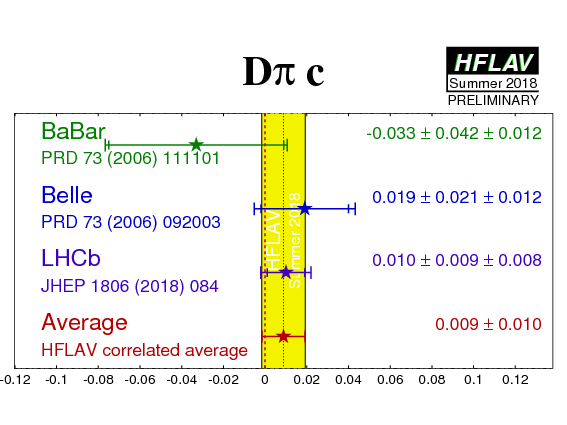
| D−+π+− |
BaBar
N(BB)=232M |
−0.010 ± 0.023 ± 0.007 | −0.033 ± 0.042 ± 0.012 | - | PRD 73 (2006) 111101 |
|
Belle
N(BB)=386M |
−0.050 ± 0.021 ± 0.012 | 0.019 ± 0.021 ± 0.012 | - | PRD 73 (2006) 092003 | |
|
LHCb
∫Ldt=3 fb−1 |
−0.048 ± 0.018 ± 0.005 | 0.010 ± 0.009 ± 0.008 | 0.00 (stat) −0.46 (syst) | JHEP 1806 (2018) 084 | |
| Average | −0.038 ± 0.013 | 0.009 ± 0.010 | −0.05 |
HFLAV correlated average
χ2 = 3.0/4 dof (CL=0.56 ⇒ 0.6σ) |
|
|
|

eps.gz png |
eps.gz png |

eps.gz png |
||
| Mode | Experiment | a | c | Reference |
|---|---|---|---|---|
|
D*−+π+− Full reconstruction |
BaBar
N(BB)=232M |
−0.040 ± 0.023 ± 0.010 | 0.049 ± 0.042 ± 0.015 | PRD 73 (2006) 111101 |
|
Belle
N(BB)=386M |
−0.039 ± 0.020 ± 0.013 | −0.011 ± 0.020 ± 0.013 | PRD 73 (2006) 092003 | |
|
D*−+π+− Partial reconstruction |
BaBar
N(BB)=232M |
−0.034 ± 0.014 ± 0.009 | −0.019 ± 0.022 ± 0.013 | PRD 71 (2005) 112003 |
|
Belle
N(BB)=657M |
−0.046 ± 0.013 ± 0.015 | −0.015 ± 0.013 ± 0.015 | PRD 84 (2011) 021101(R) | |
|
D*−+π+− All |
Average |
−0.039 ± 0.010
χ2 = 0.2/3 dof (CL=0.97 ⇒ 0.03σ) |
−0.010 ± 0.013
χ2 = 1.9/3 dof (CL=0.0.59 ⇒ 0.6σ) |
HFLAV |
|
|
eps.gz png |

eps.gz png |
. | |
| D−+ρ+− |
BaBar
N(BB)=232M |
−0.024 ± 0.031 ± 0.009 | −0.098 ± 0.055 ± 0.018 | PRD 73 (2006) 111101 |
| Compilation of the above results. |

eps.gz png |

eps.gz png |
Time-dependent analyses of transitions such as Bd → D+−KSπ−+ can be used to probe sin(2β+γ) ≡ sin(2φ1+φ3) in a similar way to that discussed above. Since the final state contains three particles, a Dalitz plot analysis is necessary to maximise the sensitivity. BaBar have carried out such an analysis. They obtain 2β+γ = (83 ± 53 ± 20)° (with an ambiguity 2β+γ → 2β+γ+π) assuming the ratio of the b → u and b → c amplitude to be constant across the Dalitz plot at 0.3.
LHCb have measured the time-dependent CP violation parameters in B0s → D−+sK+− decays. Moreover, LHCb have also studied time-dependent CP violation in B0s → D−+sK+−π+π− decays. In the latter analysis, both model-dependent and -independent analysis are done; results for the latter are quoted. These are given in terms of the quasi-two-body parameters (Cf, AΔΓf, AΔΓf, Sf, Sf), but in this case it should be understood that these are effective parameters, integrated over the phase space of the B0s → D−+sK+−π+π− decay.
| Mode | Experiment | Cf | AΔΓf | AΔΓf | Sf | Sf | Correlation | Reference |
|---|---|---|---|---|---|---|---|---|
| B0s → D−+sK+− |
LHCb Run 1
∫Ldt=3 fb−1 |
0.73 ± 0.14 ± 0.05 | 0.39 ± 0.28 ± 0.15 | 0.31 ± 0.28 ± 0.15 | −0.52 ± 0.20 ± 0.07 | −0.49 ± 0.20 ± 0.07 | (stat) (syst) | JHEP 1803 (2018) 059 |
|
LHCb Run 2
∫Ldt=6 fb−1 |
0.791 ± 0.061 ± 0.022 | 0.051 ± 0.134 ± 0.037 | 0.303 ± 0.125 ± 0.036 | −0.571 ± 0.084 ± 0.023 | −0.503 ± 0.084 ± 0.003 | (stat) (syst) | LHCb-CONF-2023-004 | |
| Average | 0.782 ± 0.059 | 0.104 ± 0.127 | 0.306 ± 0.120 | −0.565 ± 0.081 | −0.502 ± 0.078 | (stat) |
HFLAV correlated average
χ2 = 1.5/5 dof (CL=0.91 ⇒ 0.1σ) |
|
| B0s → D−+sK+−π+π− |
LHCb
∫Ldt=9 fb−1 |
0.631 ± 0.096 ± 0.032 | −0.334 ± 0.232 ± 0.097 | −0.695 ± 0.215 ± 0.081 | −0.424 ± 0.135 ± 0.033 | −0.463 ± 0.134 ± 0.031 | (stat), (syst) | JHEP 2103 (2021) 137 |
Digression:
|
Constraining γ
|
A theoretically clean measurement of the angle γ ≡ φ3 can be obtained from the rate and asymmetry measurements of B− → D(*)CPK(*)− decays, where the D(*) meson decays to CP even (D(*)CP+) and CP odd (D(*)CP−) eigenstates. The method benefits from the interference between the dominant b→cu-bar s transitions with the corresponding doubly CKM-suppressed b→uc-bar s transition. It was proposed by Gronau, Wyler and Gronau, London (GLW).
BaBar, Belle, CDF and LHCb use consistent definitions for ACP+− and RCP+−, where
| ACP+− = [Γ(B− → D(*)CP+−K(*)−) − Γ(B+ → D(*)CP+−K(*)+)] / Sum , |
| RCP+− = 2 [Γ(B− → D(*)CP+−K(*)−) + Γ(B+ → D(*)CP+−K(*)+)] / [Γ(B− → D(*)0 K(*)−) + Γ(B+ → D(*)0-bar K(*)+)]. |
Experimentally, it is often convenient to measure RCP+− using double ratios, in which similar ratios for B− → D(*) π(*)− decays are used for normalization. These double ratios are equivalent to RCP+− in the limit of vanishing b → u transition in the normalisation channel.
These observables have been measured so far for three D(*)K(*)− modes.
For the DK*− mode some care is needed due to other possible contributions to the B− → DKSπ− final state. This can be handled in the relations between the observables and γ ≡φ3 through the introduction of a coherence factor, as discussed below. It is assumed that the selection of the K* region of the DKSπ− Dalitz plot is the same for all experiments, so that the combination of results is valid.
At present we do not rescale the results to a common set of input parameters. Also, common systematic errors are not considered.
| Mode | Experiment | ACP+ | ACP− | RCP+ | RCP− | Correlations | Reference |
|---|---|---|---|---|---|---|---|
| DCPK− |
BaBar
N(BB)=467M |
0.25 ± 0.06 ± 0.02 | −0.09 ± 0.07 ± 0.02 | 1.18 ± 0.09 ± 0.05 | 1.07 ± 0.08 ± 0.04 | - | PRD 82 (2010) 072004 |
|
Belle + Belle II
N(BB)=970M |
0.125 ± 0.058 ± 0.014 | −0.167 ± 0.057 ± 0.006 | 1.164 ± 0.081 ± 0.036 | 1.151 ± 0.074 ± 0.019 | (stat) (syst) | arXiv:2308.05048 | |
|
CDF
∫Ldt=1 fb−1 |
0.39 ± 0.17 ± 0.04 | - | 1.30 ± 0.24 ± 0.12 | - | - | PRD 81 (2010) 031105(R) | |
|
LHCb
∫Ldt=8.7 fb−1 |
0.136 ± 0.009 ± 0.001 | - | 0.950 ± 0.009 ± 0.010 | - | (stat), (syst) | JHEP 2104 (2021) 081 | |
| Average |
0.139 ± 0.009
χ2 = 5.3/3 dof (CL=0.15 ⇒ 1.4σ) |
−0.138 ± 0.045
χ2 = 0.69 (CL=0.41 ⇒ 0.8σ) |
0.959 ± 0.013
χ2 = 12/3 dof (CL=0.007 ⇒ 2.7σ) |
1.117 ± 0.058
χ2 = 0.5 (CL=0.49 ⇒ 0.7σ) |
HFLAV uncorrelated averages | ||
|
|
eps.gz png | eps.gz png | eps.gz png | eps.gz png | . | ||
| Click here for averages excluding KSφ from the CP-odd channels. | |||||||
| D*CPK− |
BaBar
N(BB)=383M |
−0.11 ± 0.09 ± 0.01 | 0.06 ± 0.10 ± 0.02 | 1.31 ± 0.13 ± 0.03 | 1.09 ± 0.12 ± 0.04 | - | PRD 78, 092002 (2008) |
|
Belle
(*)
N(BB)=275M |
−0.20 ± 0.22 ± 0.04 | 0.13 ± 0.30 ± 0.08 | 1.41 ± 0.25 ± 0.06 | 1.15 ± 0.31 ± 0.12 | - | PRD 73 (2006) 051106 | |
|
LHCb
∫Ldt=8.7 fb−1 |
−0.115 ± 0.019 ± 0.009 | 0.123 ± 0.054 ± 0.031 | 1.051 ± 0.022 ± 0.028 | 0.952 ± 0.062 ± 0.065 | (stat), (syst) | JHEP 2104 (2021) 081 | |
| Average | −0.109 ± 0.019 | 0.096 ± 0.052 | 1.077 ± 0.034 | 1.011 ± 0.071 | (stat) |
HFLAV correlated average
χ2 = 6.5/8 dof (CL=0.59 ⇒ 0.5σ) |
|
|
|
eps.gz png | eps.gz png | eps.gz png | eps.gz png | . | ||
| DCPK*− |
BaBar
N(BB)=379M |
0.09 ± 0.13 ± 0.06 | −0.23 ± 0.21 ± 0.07 | 2.17 ± 0.35 ± 0.09 | 1.03 ± 0.27 ± 0.13 | - | PRD 80 (2009) 092001 |
| Belle | NO RESULTS AVAILABLE (*) | - | |||||
|
LHCb KK
∫Ldt=4.8 fb−1 |
0.06 ± 0.07 ± 0.01 | - | 1.22 ± 0.09 ± 0.01 | - | - | JHEP 11 (2017) 156 | |
|
LHCb pipi
∫Ldt=4.8 fb−1 |
0.15 ± 0.13 ± 0.02 | - | 1.08 ± 0.14 ± 0.03 | - | - | JHEP 11 (2017) 156 | |
| Average |
0.08 ± 0.06
χ2 = 0.37 (CL=0.83 ⇒ 0.21σ) |
−0.23 ± 0.22 |
1.22 ± 0.07
χ2 = 7.9 (CL=0.02 ⇒ 2.3σ) |
1.03 ± 0.30 | HFLAV uncorrelated avearges | ||
|
|
eps.gz png | . | eps.gz png | . | . | ||
| DCPK−π+π− |
LHCb KK
∫Ldt=3 fb−1 |
−0.045 ± 0.064 ± 0.011 | - | 1.043 ± 0.069 ± 0.034 | - | - | PRD 92 (2015) 112005 |
|
LHCb ππ
∫Ldt=3 fb−1 |
−0.054 ± 0.101 ± 0.011 | - | 1.035 ± 0.108 ± 0.038 | - | - | ||
(*) We do not include preliminary results from Belle on DCPK*− (BELLE-CONF-0316), on DCPK− (LP 2011 preliminary) or on D*CPK− (CKM 2012 preliminary) which are all unpublished after more than two years.
| Compilation of the above results. |

eps.gz png |

eps.gz png |
| CP+ only |
eps.gz png |
eps.gz png |
| CP- only |
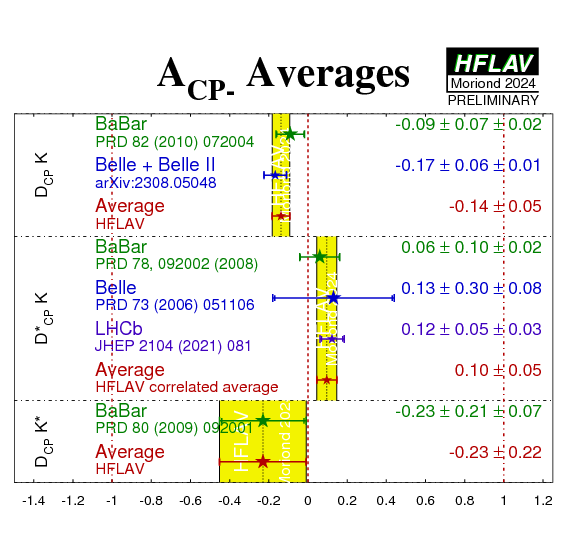
eps.gz png |

eps.gz png |
Digression:
Constraining γ ≡ φ3:
The rate ratios and asymmetries of the GLW method can be
expressed in terms of amplitude ratios and strong phase differences,
as well as the weak phase difference γ ≡ φ3.
For the GLW observables, one has:
where rB = |A(b→u)/A(b→c)| and δB = arg[A(b→u)/A(b→c)]. Only the weak phase difference γ ≡ φ3 is universal, while the other parameters depend on the decay process. In addition, the Cartesian coordinates x± (discussed below in the context of analysis of B→DK with multibody D decay) can be extracted from the observables measured in GLW analysis. The relations are
There is no direct sensitivity to y+−, but indirect bounds can be obtained using
|
If a multibody D decay can be shown to be dominated by one CP-eigenstate, it can be used in a "GLW-like" (sometimes called "quasi-GLW") analysis. The same observables RCP, ACP as for the GLW case are measured, but an additional factor of (2F+-1), where F+ is the fractional CP-even content, enters the expressions relating these observables to γ ≡ φ3. The F+ factors have been measured, with first measurements using CLEOc data (see also here) and more recent and precise results from BESIII (also here)
The GLW-like observables for D→π+π−π0 and K+K−π0 have been measured by LHCb. The AGLW observable for D→π+π−π0 was measured in an earlier analysis (discussed more below) by BaBar. The GLW-like observables for D→π+π−π+π− have been measured by LHCb.
| Mode | Experiment | AGLW | RGLW | Reference |
|---|---|---|---|---|
| Dπππ0K− |
LHCb
∫Ldt=9 fb−1 |
0.109 ± 0.043 ± 0.003 | 0.902 ± 0.041 ± 0.004 | JHEP 07 (2022) 099 |
|
BaBar
N(BB)=324M |
−0.02 ± 0.15 ± 0.03 | - | PRL 99 (2007) 251801 | |
| Average |
0.100 ± 0.041
χ2 = 0.7 (CL=0.42 ⇒ 0.8σ) |
0.902 ± 0.041 | HFLAV | |
|
|
eps.gz png | . | . | |
| DKKπ0K− |
LHCb
∫Ldt=9 fb−1 |
0.067 ± 0.073 ± 0.003 | 1.021 ± 0.079 ± 0.005 | JHEP 07 (2022) 099 |
| DππππK− |
LHCb
∫Ldt=9 fb−1 |
0.061 ± 0.013 ± 0.002 | 0.978 ± 0.014 ± 0.010 | EPJ C83 (2023) 547 |
| DKKππK− (*) |
LHCb
∫Ldt=9 fb−1 |
0.095 ± 0.023 ± 0.002 | 0.974 ± 0.024 ± 0.015 | EPJ C83 (2023) 547 |
| DππππK*− |
LHCb
∫Ldt=4.8 fb−1 |
0.02 ± 0.11 ± 0.01 | 1.08 ± 0.13 ± 0.03 | JHEP 1711 (2017) 156 |
(*) Results from a binned analysis of B−→DKKππK− based on the same data sample are reported below.
| Compilation of the above results together with those for CP-even modes. |

eps.gz png |
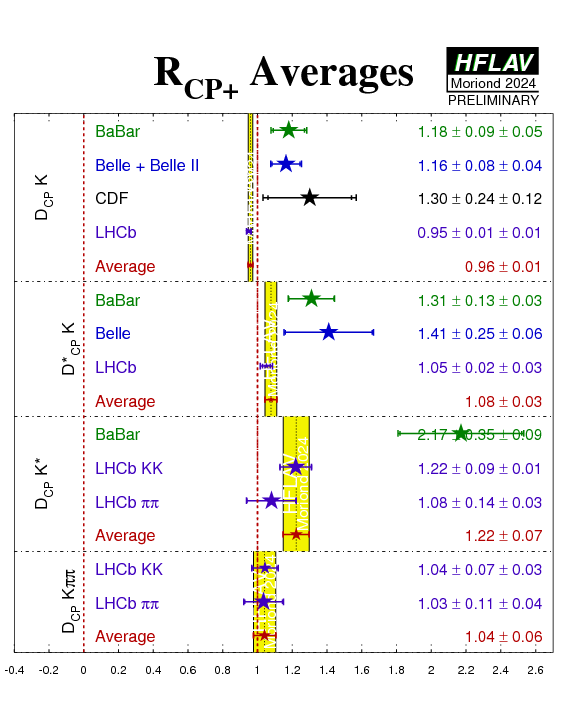
eps.gz png |
In the limit that a multibody decay is a pure CP-eigenstate, there is no benefit to analysing the distribution of the decays across the phase space (i.e. of performing analyses such as those discussed below), but otherwise additional sensitivity can be obtained. BaBar have performed an analysis of the D decay Dalitz plot in the decay chain B− → D K−, D → π+π−π0. Since a significant contribution to the sensitivity to CP violation comes from the AGLW observable, this information is included into the fit via a choice of fit parameters that avoids significant biasing and nonlinear correlations. The result is parameterized in terms of polar coordinates:
| ρ± ≡ | z± - x0 | | θ± ≡ tan− 1 (Im(z±) / (Re(z±) - x0)) |
where the constant x0 = 0.850 depends on the amplitude structure of the D → π+π−π0 decay (x0 ≡ 2F+ - 1, where F+ is the fractional CP-even content defined above), and z± = rB ei( δB ± γ ) ≡ rB ei( δB ± φ3 ). This choice of variables is motivated by the fact that the yields of B± decays are proportional to 1 + ρ±2 - x02. The uncertainty due to the D decay model is included in the systematic error.
| Mode | Experiment | ρ+ | θ+ | ρ− | θ− | Reference |
|---|---|---|---|---|---|---|
|
DK−
D→ π+π−π0 |
BaBar
N(BB)=324M |
0.75 ± 0.11 ± 0.04 | (147 ± 23 ± 1)° | 0.72 ± 0.11 ± 0.04 | (173 ± 42 ± 2)° | PRL 99 (2007) 251801 |
Digression:
|
Constraining γ ≡ φ3:
The measurements of ρ+,− and θ+,− can be used to place bounds on γ ≡ φ3 and the hadronic parameters. BaBar use a frequentist technique to obtain −30° < γ < 76°, 0.06 < rB (DK−) < 0.78 and −27° < δ B (DK−) < 78° at the 68% confidence level. |
A modification of the GLW idea has been suggested by Atwood, Dunietz and Soni, where B− → DK− with D → K+π− (or similar) and the charge conjugate decays are used. Here, the favoured (b→c) B decay followed by the doubly CKM-suppressed D decay interferes with the suppressed (b→u) B decay followed by the CKM-favored D decay. The relative similarity of the combined decay amplitudes enhances the possible CP asymmetry. The experiments use consistent definitions for AADS and RADS, where (for example for the B− → DK−, D → K+π− mode)
| AADS = [Γ(B− → [K+π−]DK−) − Γ(B+ → [K−π+]DK+)] / [Γ(B− → [K+π−]DK−) + Γ(B+ → [K−π+]DK+)] , |
| RADS = [Γ(B− → [K+π−]DK−) + Γ(B+ → [K−π+]DK+)] / [Γ(B− → [K−π+]DK−) + Γ(B+ → [K+π−]DK+)] . |
Digression:
|
It has been noted that the observables (R+, R−) may be more suitable for use than (RADS, AADS) since the former are better behaved (they are statistically independent observables, while the uncertainty on AADS depends on the central value of RADS). On the other hand, the (R+, R−) parametrisation tends to be associated with larger systematic correlations than (RADS, AADS). The definitions are |
|
R+ = Γ(B+ → [K−π+]DK+) / Γ(B+ → [K+π−]DK+) R− = Γ(B− → [K+π−]DK−) / Γ(B− → [K−π+]DK−) |
|
They are related to (RADS, AADS) by |
|
RADS = (R+ + R−)/2 AADS = (R− − R+) / (R− + R+) |
|
We may switch to using this set of variables at a later time, but presently the majority of experimental results are presented in the (RADS, AADS) format. |
(Some of) these observables have been measured so far for the D(*)K(*)− modes. BaBar, Belle, CDF and LHCb have presented results for B− → DK− while BaBar and Belle have also presented results using B− → D*K−, with both D* → Dπ0 and D* → Dγ. LHCb have also presented results for B− → D*K− using a partial reconstruction technique that provides statistical separation between the D* → Dπ0 and D* → Dγ decays (and certain backgrounds); the corresponding observables are therefore correlated. BaBar have also presented results on B− → DK*−. For all the above the D → K+π− mode is used. In addition, BaBar and LHCb have presented results using B− → DK− with D → K+π−π0 and LHCb have presented results using B− → DK− with D → K+π−π+π−.
The primary results of the LHCb analysis of B− → D(*)K− with D → K+π− are the (R−, R+) observables mentioned above, for which separate statistical and systematic uncertainties are reported. We take the results in terms of (RADS, AADS), for which only total uncertainties are given, in order to be able to average with results from other experiments.
At present we do not rescale the results to a common set of input parameters. Also, common systematic errors are not considered.
| Mode | Experiment | AADS | RADS | Reference | |
|---|---|---|---|---|---|
|
DK−
D→Kπ |
BaBar
N(BB)=467M |
−0.86 ± 0.47 +0.12 −0.16 | 0.011 ± 0.006 ± 0.002 | PRD 82 (2010) 072006 | |
|
Belle
N(BB)=772M |
−0.39 +0.26 −0.28 +0.04 −0.03 | 0.0163 +0.0044 −0.0041 +0.0007 −0.0013 | PRL 106 (2011) 231803 | ||
|
CDF
∫Ldt=7 fb−1 |
−0.82 ± 0.44 ± 0.09 | 0.0220 ± 0.0086 ± 0.0026 | PRD 84 (2011) 091504 | ||
|
LHCb
∫Ldt=8.7 fb−1 |
−0.451 ± 0.026 | 0.0173 ± 0.0006 | JHEP 2104 (2021) 081 | ||
| Average |
−0.453 ± 0.026
χ2 = 1.4/3 dof (CL=0.70 ⇒ 0.4σ) |
0.0172 ± 0.0006
χ2 = 1.3/3 dof (CL=0.73 ⇒ 0.4σ) |
HFLAV | ||
|
|
eps.gz png | eps.gz png | . | ||
|
DK−
D→Kππ0 |
BaBar
N(BB)=474M |
- | 0.0091 +0.0082 −0.0076 +0.0014 −0.0037 | PRD 84 (2011) 012002 | |
|
Belle
N(BB)=772M |
0.41 ± 0.30 ± 0.05 | 0.0198 ± 0.0062 ± 0.0024 | PRD 88 (2013) 091104(R) | ||
|
LHCb
∫Ldt=9 fb−1 |
−0.38 ± 0.12 ± 0.02 | 0.0127 ± 0.0016 ± 0.0002 | JHEP 07 (2022) 099 | ||
| Average |
−0.27 ± 0.11
χ2 = 5.8 (CL=0.016 ⇒ 2.4σ) |
0.0130 ± 0.0015
χ2 = 1.3/2 dof (CL=0.52 ⇒ 0.6σ) |
HFLAV | ||
|
|
. eps.gz png | eps.gz png | . | ||
|
DK−
D→K3π |
LHCb
(**)
∫Ldt=9 fb−1 |
−0.321 ± 0.039 ± 0.005 | 0.0133 ± 0.0006 ± 0.0001 | JHEP 07 (2023) 138 | |
|
D*K−
D* → Dπ0 D→Kπ |
BaBar
N(BB)=467M |
0.77 ± 0.35 ± 0.12 | 0.018 ± 0.009 ± 0.004 | PRD 82 (2010) 072006 | |
| Belle | NO RESULTS AVAILABLE (*) | - | |||
|
LHCb
∫Ldt=8.7 fb−1 |
0.717 ± 0.286 | 0.0118 ± 0.0034 | JHEP 2104 (2021) 081 | ||
| Average |
0.74 ± 0.23
χ2 = 0.01 (CL=0.91 ⇒ 0.1σ) |
0.0125 ± 0.0032
χ2 = 0.4 (CL=0.55 ⇒ 0.6σ) |
HFLAV | ||
|
|
eps.gz png | eps.gz png | . | ||
|
D*K−
D* → Dγ D→Kπ |
BaBar
N(BB)=467M |
0.36 ± 0.94 +0.25 −0.41 | 0.013 ± 0.014 ± 0.008 | PRD 82 (2010) 072006 | |
| Belle | NO RESULTS AVAILABLE (*) | - | |||
|
LHCb
∫Ldt=8.7 fb−1 |
−0.558 ± 1.349 | 0.0163 ± 0.0373 | JHEP 2104 (2021) 081 | ||
| Average |
0.03 ± 0.81
χ2 = 0.3 (CL=0.59 ⇒ 0.6σ) |
0.0135 ± 0.0148
χ2 = 0.01 (CL=0.94 ⇒ 0.1σ) |
HFLAV | ||
|
|
eps.gz png | eps.gz png | . | ||
|
DK*−
D→Kπ |
BaBar
N(BB)=379M |
−0.34 ± 0.43 ± 0.16 | 0.066 ± 0.031 ± 0.010 | PRD 80 (2009) 092001 | |
|
LHCb
∫Ldt=4.8 fb−1 |
−0.81 ± 0.17 ± 0.04 | 0.011 ± 0.004 ± 0.001 | JHEP 1711 (2017) 156 | ||
| Average |
−0.75 ± 0.16
χ2 = 0.92 (CL=0.34 ⇒ 1.0σ) |
0.012 ± 0.004
χ2 = 2.8 (CL=0.09 ⇒ 1.7σ) |
HFLAV | ||
|
|
eps.gz png | eps.gz png | . | ||
|
DK*−
D→K3π |
LHCb
∫Ldt=4.8 fb−1 |
−0.45 ± 0.21 ± 0.14 | 0.011 ± 0.005 ± 0.003 | JHEP 1711 (2017) 156 | |
|
DK−π+π−
D→Kπ |
LHCb
∫Ldt=3 fb−1 |
−0.32 +0.27 −0.34 | 0.0082 +0.0038 −0.0030 | PRD 92 (2015) 112005 | |
(*)
We do not include preliminary results from
Belle on B− → D*K−, D* → Dπ0 or Dγ, D→Kπ (LP 2011 preliminary)
which are unpublished after more than two years.
(**)
LHCb have also performed a binned analysis of B → DK, D → K3π, with the same data sample. The unbinned and binned measurements are not independent and therefore should not be combined. The binned analysis has more sensitivity to γ ≡ φ3.
| Compilation of the above results. |
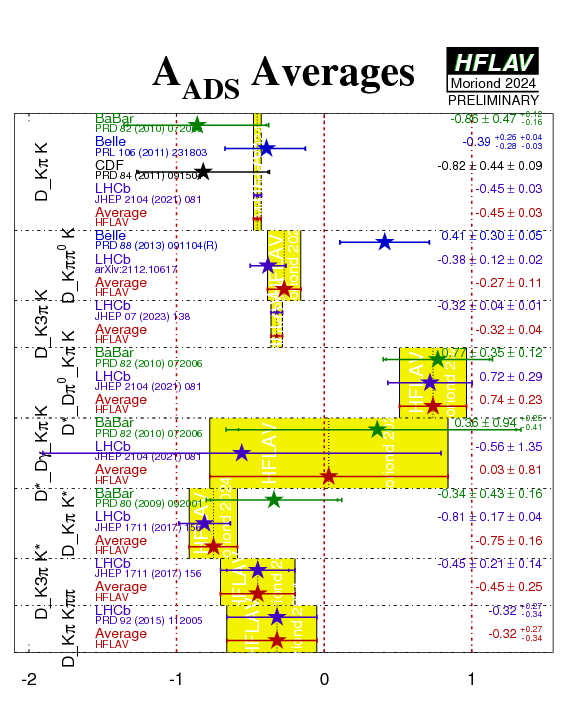
eps.gz png |

eps.gz png |
Digression:
|
Constraining γ ≡ φ3: As for the GLW method, the rate ratios and asymmetries of the ADS method can be expressed in terms of amplitude ratios and strong phase differences, as well as the weak phase difference γ ≡ φ3. For the ADS observables, one has:
where rB = |A(b→u)/A(b→c)| and δB = arg[A(b→u)/A(b→c)] as before. rD and δD are the corresponding amplitude ratio and strong phase difference of the D meson decay amplitudes. The value of rD2 is obtained from the ratio of the suppressed-to-allowed branching fractions, ensuring that mixing effects are corrected for. The value of δD can be determined directly using quantum correlated D mesons produced in ψ(3770) decay, as has been done by CLEO. The most precise values of both quantities come from the averages performed by HFLAV to obtain the mixing parameters in the charm system. The strong phase, δB, is different, in general, for decays to D and D* mesons. Bondar and Gershon have pointed out that there is an effective strong phase shift of π between the cases that D* is reconstructed in the Dπ0 and Dγ final states, which in principle allows γ ≡ φ3 to be measured using the ADS technique with B+− → D* K+− alone. In the case of D decay to a multibody D final state, such K+π−π0 or K+π−π+π−, the relations between the observables and γ ≡ φ3 are modified by the introduction of a coherence factor. These parameters have been determined in arXiv:1602.07430, combining results from CLEOc and LHCb data. The modification to the formalism is similar to that discussed for "GLW-like" analyses above, but since the possibility to use multibody decays was considered in the original ADS papers, it is not usually referred to as "ADS-like" (or "quasi-ADS"). |
As can be seen from the expressions above, the maximum size of the asymmetry, for given values of rB and rD is given by: AADS (max) = 2rBrD / (rB2+rD2). Thus, sizeable asymmetries may be found also for B− → D(*)π− decays, despite the expected smallness (~0.01) of rB for this case, providing sensitivity to γ ≡ φ3. Some of the observables have been measured by BaBar, Belle, CDF and LHCb in the various D(*)π− modes.
| Mode | Experiment | AADS | RADS | Reference | |
|---|---|---|---|---|---|
|
Dπ−
D→Kπ |
BaBar
N(BB)=467M |
0.03 ± 0.17 ± 0.04 | 0.0033 ± 0.0006 ± 0.0004 | PRD 82 (2010) 072006 | |
|
Belle
N(BB)=772M |
−0.04 ± 0.11 +0.02 −0.01 | 0.00328 +0.00038 −0.00036 +0.00012 −0.00018 | PRL 106 (2011) 231803 | ||
|
CDF
∫Ldt=7 fb−1 |
0.13 ± 0.25 ± 0.02 | 0.0028 ± 0.0007 ± 0.0004 | PRD 84 (2011) 091504 | ||
|
LHCb
∫Ldt=8.7 fb−1 |
0.129 ± 0.014 | 0.00368 ± 0.00007 | JHEP 2104 (2021) 081 | ||
| Average |
0.126 ± 0.014
χ2 = 2.6/3 dof (CL=0.47 ⇒ 0.7σ) |
0.00366 ± 0.00007
χ2 = 2.4/3 dof (CL=0.50 ⇒ 0.7σ) |
HFLAV | ||
|
|
eps.gz png | eps.gz png | . | ||
|
Dπ−
D → Kππ0 |
Belle
N(BB)=772M |
0.16 ± 0.27 +0.03 −0.04 | 0.00189 ± 0.00054 +0.00022 −0.00025 | PRD 88 (2013) 091104(R) | |
|
LHCb
∫Ldt=9 fb−1 |
0.069 ± 0.094 ± 0.016 | 0.00207 ± 0.00020 ± 0.00003 | JHEP 07 (2022) 099 | ||
| Average |
0.08 ± 0.09
χ2 = 0.10 (CL=0.75 ⇒ 0.3σ) |
0.00205 ± 0.00019
χ2 = 0.08 (CL=0.77 ⇒ 0.3σ) |
HFLAV | ||
|
|
eps.gz png | eps.gz png | . | ||
|
Dπ−
D → K3π |
LHCb
∫Ldt=3 fb−1 |
0.070 ± 0.019 ± 0.006 | 0.00345 ± 0.00007 ± 0.00001 | JHEP 07 (2023) 138 | |
|
D*π−
D* → Dπ0 D→Kπ |
BaBar
N(BB)=467M |
−0.09 ± 0.27 ± 0.05 | 0.0032 ± 0.0009 ± 0.0008 | PRD 82 (2010) 072006 | |
| Belle | NO RESULTS AVAILABLE (*) | - | |||
|
LHCb
∫Ldt=8.7 fb−1 |
−0.140 ± 0.059 | 0.00471 ± 0.00077 | JHEP 2104 (2021) 081 | ||
| Average |
−0.138 ± 0.058
χ2 = 0.032 (CL=0.86 ⇒ 0.2σ) |
0.00427 ± 0.00065
χ2 = 1.1 (CL=0.29 ⇒ 1.1σ) |
HFLAV | ||
|
|
eps.gz png | eps.gz png | . | ||
|
D*π−
D* → Dγ D→Kπ |
BaBar
N(BB)=467M |
−0.65 ± 0.55 ± 0.22 | 0.0027 ± 0.0014 ± 0.0022 | PRD 82 (2010) 072006 | |
| Belle | NO RESULTS AVAILABLE (*) | - | |||
|
LHCb
∫Ldt=8.7 fb−1 |
0.079 ± 0.128 | 0.00420 ± 0.00138 | JHEP 2104 (2021) 081 | ||
| Average |
0.046 ± 0.125
χ2 = 1.4 (CL=0.23 ⇒ 1.2σ) |
0.00387 ± 0.00122
χ2 = 0.26 (CL=0.61 ⇒ 0.5σ) |
HFLAV | ||
|
|
eps.gz png | eps.gz png | . | ||
|
D3π−
D→Kπ |
LHCb
∫Ldt=3 fb−1 |
−0.003 ± 0.090 | 0.00427 ± 0.00043 | PRD 92 (2015) 112005 | |
(*) We do not include preliminary results from Belle on B− → D*π−, D* → Dπ0 or Dγ, D→Kπ (LP 2011 preliminary) which are unpublished after more than two years.
| Compilation of the above results. |

eps.gz png |
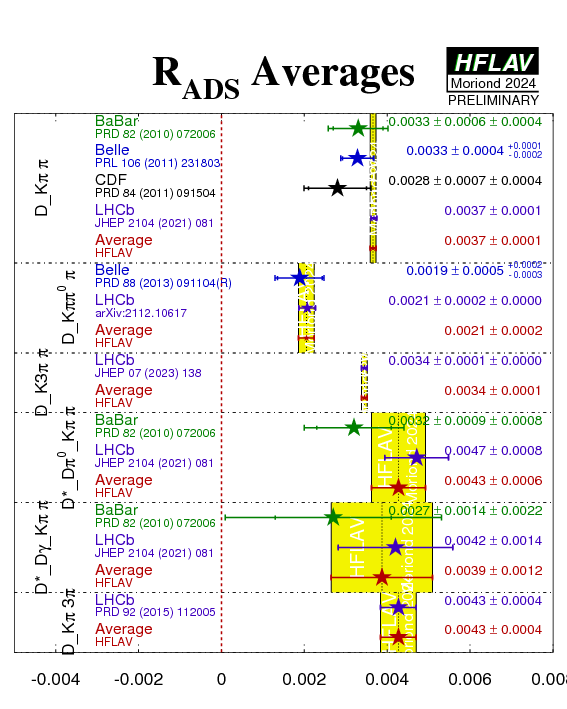
eps.gz png |
For multibody D decays involving interference between Cabibbo-favoured and doubly-Cabibbo-suppressed amplitudes, improved sensitivity can be obtained by binning the phase space and measuring the ADS observables in each bin. The sensitivity of γ ≡ φ3 to the observables follows the same equations as for the unbinned case, with each bin having independent hadronic parameters (coherence factor, and the effective ratio of and strong phase difference between amplitudes, integrated over the bin). Constraints on these hadronic parameters can be obtained from quantum-correlated ψ(3770) → D0D0 events.
LHCb have measured these parameters with both B− → DK− and B− → Dπ− decays with D → K−+π+−π+π+. A binning scheme with four bins, defined in arXiv:1909.10196 is used.
| Measurement |
LHCb B− → DK− (*)
∫L=9 fb−1 |
LHCb B− → Dπ− (*)
∫L=9 fb−1 |
|---|---|---|
| R−1 | 0.00589 +0.00125 −0.00114 ± 0.00012 | 0.00426 +0.00021 −0.00020 ± 0.00004 |
| R+1 | 0.01656 +0.00179 −0.00170 ± 0.00020 | 0.00358 +0.00020 −0.00019 ± 0.00004 |
| R−2 | 0.00241 +0.00111 −0.00098 ± 0.00014 | 0.00452 +0.00024 −0.00023 ± 0.00005 |
| R+2 | 0.02412 +0.00230 −0.00219 ± 0.00028 | 0.00368 ± 0.00022 ± 0.00004 |
| R−3 | 0.01199 +0.00176 −0.00164 ± 0.00019 | 0.00429 +0.00023 −0.00022 ± 0.00005 |
| R+3 | 0.02091 +0.00212 −0.00201 ± 0.00025 | 0.00359 +0.00022 −0.00021 ± 0.00004 |
| R−4 | 0.01371 +0.00155 −0.00147 ± 0.00017 | 0.00194 +0.00015 −0.00014 ± 0.00003 |
| R+4 | 0.01084 +0.00145 −0.00136 ± 0.00016 | 0.00211 ± 0.00015 ± 0.00003 |
| Correlations | (stat) (syst) | (stat) (syst) |
| Reference | JHEP 2307 (2023) 138 | |
(*) These results do not include corrections of O(1%) due to efficiency variation across the phase-space bins, which can be different for the numerator and denominator modes in each ratio.
Digression:
|
Constraining γ ≡ φ3:
The above results are combined with constraints on the hadronic parameters obtained from BESIII and CLEOc data to obtain results for γ ≡ φ3 and the hadronic parameters of the B decays. The hadronic parameters are quoted in terms of both (rB, δB) and (x,y) = (Re[rBexp(iδB)], Im[rBexp(iδB)]). Note that the latter are similar to the (x±,y±) parameters used for multibody self-conjugate decays below, but with the dependence on γ ≡ φ factorised out. |
|
|
LHCb obtain
γ = (54.8 +6.0−5.8 ± 0.6 +6.7−4.3 )° |
|
|
rB(DK) = (94.6 +3.1−3.1 +0.5−0.5 +3.0−2.3) × 10−3 δB(DK) = (134.6 +6.0−6.0 +0.7−0.7 +8.6−8.7)° rB(Dπ) = (4.5 +1.1−1.0 +0.3−0.3 +0.4−0.3) × 10−3 δB(Dπ) = (311.8 +14.7−15.0 +3.0−2.3 +14.7−15.0)° |
x(DK) = (−66.4 +7.6−7.2 +0.9−0.9 +10.0−7.3) × 10−3 y(DK) = (67.4 +7.1−7.5 +0.8−1.0 +11.1−12.1) × 10−3 x(Dπ) = (3.0 +1.2−1.2 +0.1−0.1 +0.9−0.9) × 10−3 y(Dπ) = (−3.4 +1.1−1.1 +0.3−0.3 +0.8−0.8) × 10−3 |
Another method to extract γ ≡ φ3 from the interference between B− → D(*)0 K− and B− → D(*)0-bar K− uses multibody D decays. A Dalitz plot analysis allows simultaneous determination of the weak phase difference γ ≡ φ3, the strong phase difference δB and the ratio of amplitudes rB. This idea was proposed by Giri, Grossman, Soffer and Zupan and Bondar and Poluektov from the Belle Collaboration. We refer to it as the BPGGSZ method (details of its development can be found at arXiv:2006.12404).
The analysis can be performed either with the assumption of a Dalitz plot model for the D meson decay (model-dependent) or without such an assumption (model-independent). In the latter case, it is necessary to bin the Dalitz plot and use measurements of quantities related to the average strong phase difference between the amplitudes D and D-bar decays in each bin. Such measurements can be obtained using ψ(3770) → D0D0 events. Note that due to the strong statistical and systematic correlations, model-dependent results and model-independent results from the same experiment cannot be combined.
If the values of γ ≡ φ3, δB and rB are obtained by directly fitting the data, the extracted value of rB is biased (since it is positive definite by nature). Since the error on γ ≡ φ3 depends on the value of rB some statistical treatment is necessary to correctly estimate the uncertainty. To obviate this effect, experiments use a different set of variables in the fits:
| x+ = rB cos( δB+γ ) ≡ rB cos( δB+φ3 ) | y+ = rB sin( δB+γ ) ≡ rB sin( δB+φ3 ) |
| x− = rB cos( δB−γ ) ≡ rB cos( δB−φ3 ) | y− = rB sin( δB−γ ) ≡ rB sin( δB−φ3 ) |
Note that (x+,y+) are determined from B+ decays, while (x−,y−) are determined from B− decays.
These parameters have the advantage of having (approximately) Gaussian distributions, and of having small statistical correlations. Some statistical treatment is necessary to convert these measurements into constraints on the underlying physical parameters γ ≡ φ3, δB and rB
Results are available from both Belle and BaBar using B− → D K−, B− → D*K− and B− → DK*−. Both BaBar and Belle use both D* decays to Dπ0 and Dγ, taking the effective strong phase shift into account. Both experiments use the decay D → KSπ+π−; BaBar also use D → KSK+K− (though not for B− → DK*−). Results are also available from LHCb using B− → D K− with D → KSπ+π−.
For the DK*− mode, both BaBar and Belle use K*− → KSπ−; in this case some care is needed due to other possible contributions to the B− → DKSπ− final state. Belle assign an additional (model) uncertainty, while BaBar using use an alternative parametrization [replacing rB and δB with κrs and δs, respectively] suggested by Gronau. [BaBar do not obtain constraints on rB and δB in this decay.]
The results below have three sets of errors, which are statistical, systematic, and model related uncertainties respectively. For details of correlations in the model uncertainty assigned by Belle, see the Appendix of their paper. The Belle results using B− → DK*− also include an additional source of uncertainty due to background from B− → DKSπ− other than B− → DK*−, which we have not included here.
Averages are performed using the following procedure.
| Mode | Experiment | x+ | y+ | x− | y− | Correlation | Reference |
|---|---|---|---|---|---|---|---|
| DK− |
BaBar
N(BB)=468M |
−0.103 ± 0.037 ± 0.006 ± 0.007 | −0.021 ± 0.048 ± 0.004 ± 0.009 | 0.060 ± 0.039 ± 0.007 ± 0.006 | 0.062 ± 0.045 ± 0.004 ± 0.006 | (stat) (syst) (model) | PRL 105 (2010) 121801 |
|
Belle
N(BB)=657M |
−0.107 ± 0.043 ± 0.011 ± 0.055 | −0.067 ± 0.059 ± 0.018 ± 0.063 | 0.105 ± 0.047 ± 0.011 ± 0.064 | 0.177 ± 0.060 ± 0.018 ± 0.054 | (stat) (model) | PRD 81 (2010) 112002 | |
|
LHCb
∫Ldt=1 fb−1 |
−0.084 ± 0.045 ± 0.009 ± 0.005 | −0.032 ± 0.048 +0.010 −0.009 ± 0.008 | 0.027 ± 0.044 +0.010 −0.008 ± 0.001 | 0.013 ± 0.048 +0.009 −0.007 ± 0.003 | (stat) (model) | NPB 888 (2014) 169 | |
| Average | −0.098 ± 0.024 | −0.036 ± 0.030 | 0.070 ± 0.025 | 0.075 ± 0.029 | (stat) |
HFLAV correlated average
χ2 = 7.2/8 dof (CL=0.52 ⇒ 0.7σ) |
|
|
NB. The contours in these plots do not include model errors. |
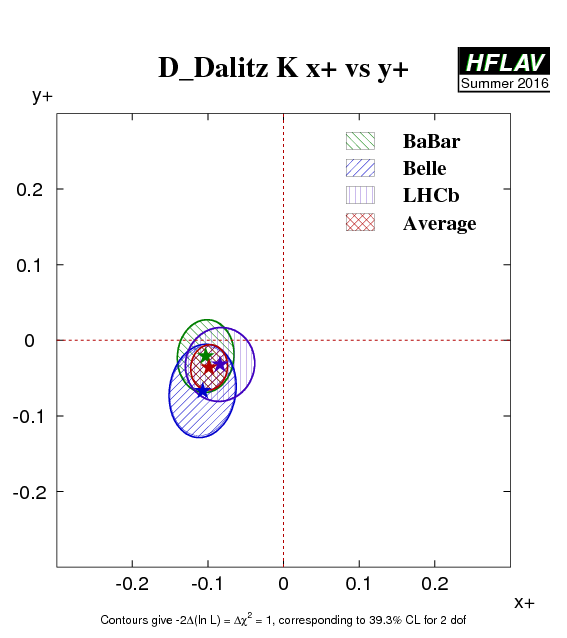
eps.gz png |

eps.gz png |
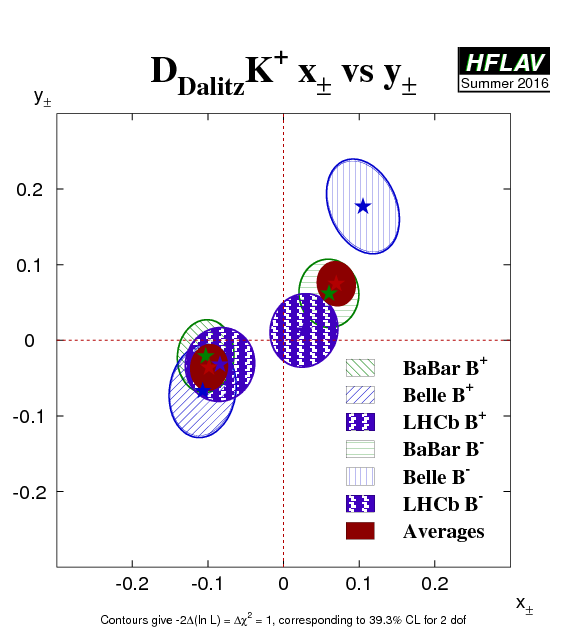
eps.gz png |
||||
| D*K− |
BaBar
N(BB)=468M |
0.147 ± 0.053 ± 0.017 ± 0.003 | −0.032 ± 0.077 ± 0.008 ± 0.006 | −0.104 ± 0.051 ± 0.019 ± 0.002 | −0.052 ± 0.063 ± 0.009 ± 0.007 | (stat) (syst) (model) | PRL 105 (2010) 121801 |
|
Belle
(*)
N(BB)=657M |
0.100 ± 0.074 ± 0.081 | 0.155 ± 0.101 ± 0.063 | −0.023 ± 0.112 ± 0.090 | −0.252 ± 0.112 ± 0.049 | (stat) (model) | PRD 81 (2010) 112002 | |
| Average No model error |
0.132 ± 0.044 | 0.037 ± 0.061 | −0.081 ± 0.049 | −0.107 ± 0.055 | (stat+syst) |
HFLAV correlated average
χ2 = 5.8/4 dof (CL=0.22 ⇒ 1.2σ) |
|
|
NB. The contours in these plots do not include model errors. |

eps.gz png |
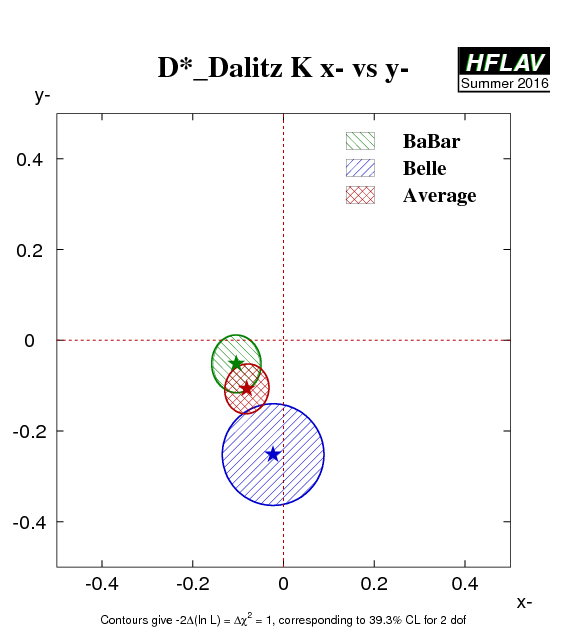
eps.gz png |
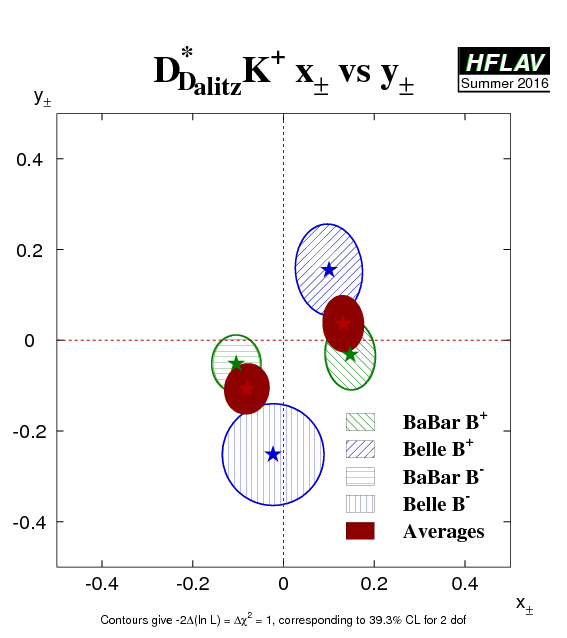
eps.gz png |
||||
| DK*− |
BaBar
N(BB)=468M |
−0.151 ± 0.083 ± 0.029 ± 0.006 | 0.045 ± 0.106 ± 0.036 ± 0.008 | 0.075 ± 0.096 ± 0.029 ± 0.007 | 0.127 ± 0.095 ± 0.027 ± 0.006 | (stat) (syst) (model) | PRL 105 (2010) 121801 |
|
Belle
N(BB)=386M |
−0.105 +0.177 −0.167 ± 0.006 ± 0.088 | −0.004 +0.164 −0.156 ± 0.013 ± 0.095 | −0.784 +0.249 −0.295 ± 0.029 ± 0.097 | −0.281 +0.440 −0.335 ± 0.046 ± 0.086 | (stat) (model) | PRD 73, 112009 (2006) | |
| Average No model error |
−0.152 ± 0.077 | 0.024 ± 0.091 | −0.043 ± 0.094 | 0.091 ± 0.096 | (stat+syst) |
HFLAV correlated average
χ2 = 13/4 dof (CL=0.011 ⇒ 2.5σ) |
|
|
NB. The contours in these plots do not include model errors. |
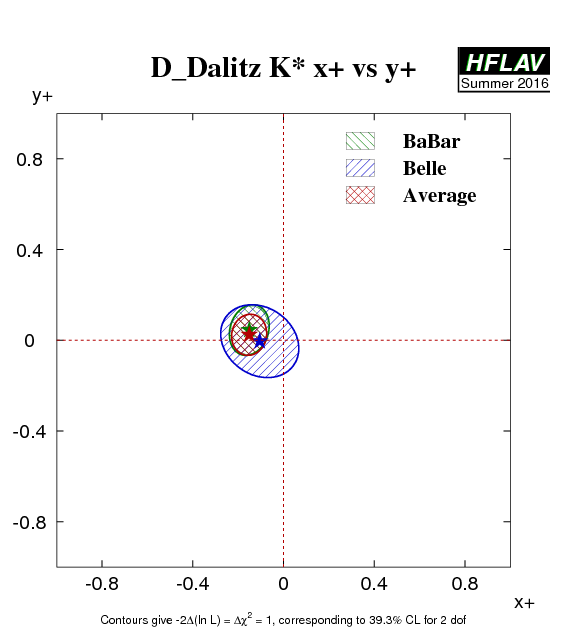
eps.gz png |
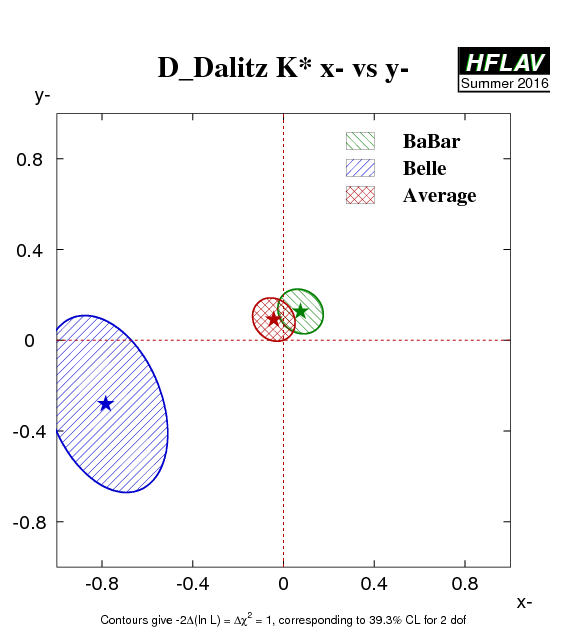
eps.gz png |

eps.gz png |
||||
(*) The Belle results for D*K− are our average of their results on D*K− with D*→Dπ0 and D*K− with D*→Dγ. The average is performed using the statistical correlations provided, and neglecting all systematic correlations; model uncertainties are not included. The first uncertainty on the quoted results is combined statistical and systematic, the second is the model error (taken from the Belle results on D*K− with D*→Dπ0).
|
Compilation of (x±,y±) measurements from B → D(*)K(*) decays with D → KSπ+π− and D → KSK+K−. NB. The uncertainities in these plots do not include model errors. |

eps.gz png |

eps.gz png |
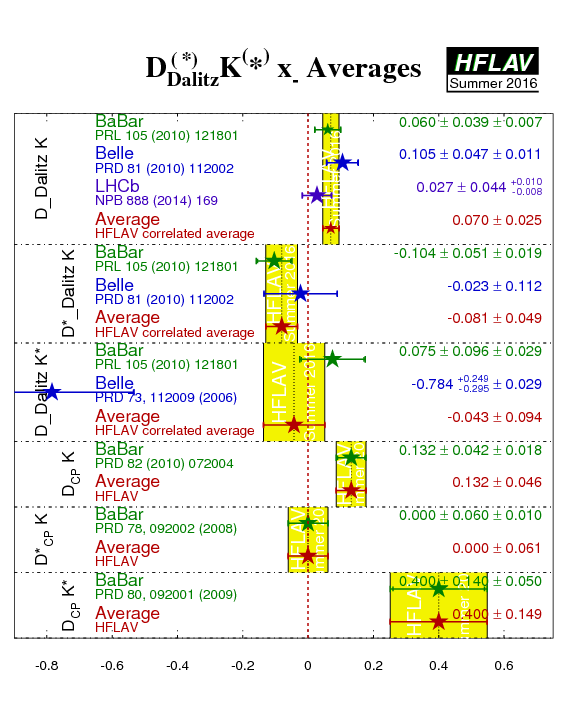
eps.gz png |

eps.gz png |
Digression:
|
Constraining γ ≡ φ3:
The measurements of x+,− and y+,− in the various D(*)K(*) decay modes can be used to place bounds on γ ≡ φ3. All experiments have done so using frequentist techniques. Note that the uncertainty on γ ≡ φ3 is approximately inversely proportional to the central value of rB. |
|||||
|
BaBar obtain
γ = (68 +15−14 ± 4 ± 3)° (from DK−, D*K− & DK*−) |
Belle obtain
φ3 = (78 +11−12 ± 4 ± 9)° (from DK− & D*K−) |
LHCb obtain
γ = (84 +49−42)° (from DK− using ∫Ldt=1 fb−1; a more precise result using ∫Ldt=3 fb−1 and the model-independent method is reported below) |
|||
| The experiments also obtain values for the hadronic parameters | |||||
| rB (DK−) = 0.096 ± 0.029 ± 0.005 ± 0.004 | δB (DK−) = (119 +19−20 ± 3 ± 3)° | rB (DK−) = 0.160 +0.040−0.038 ± 0.011+0.05−0.010 | δB (DK−) = (138 +13−16 ± 4 ± 23)° | rB (DK−) = 0.06 ± 0.04 | δB (DK−) = (115 +41−51)° |
| rB (D*K−) = 0.133 +0.042−0.039 ± 0.014 ± 0.003 | δB (D*K−) = (−82 ± 21 ± 5 ± 3)° | rB (D*K−) = 0.196 +0.072−0.069 ± 0.012 +0.062−0.012 | δB (D*K−) = (342 +19−21 ± 3 ± 23)° | . | . |
| κrs = 0.149 +0.066−0.062 ± 0.026 ± 0.006 | δs = (111 ± 32 ± 11 ± 3)° | ( rB (DK*−) = 0.56 +0.22−0.16 ± 0.04 ± 0.08 *) | (δ B (DK*−) = (243+20−23 ± 3 ± 50 )° *) | . | . |
| Note that the above results suffer an ambiguity: γ → γ + π ≡ φ3 → φ3 + π, δ → δ + π. We quote the result which is consistent with the Standard Model fit. | |||||
A model-independent approach to the analysis of B− → D(*) K− with multibody D decays was proposed by Giri, Grossman, Soffer and Zupan, and further developed by Bondar and Poluektov (see also here). The method relies on information on the average strong phase difference between D0 and D0-bar decays in bins of Dalitz plot position that can be obtained from quantum-correlated ψ(3770) → D0D0 events. This information is measured in the form of parameters ci and si that are the amplitude weighted averages of the cosine and sine of the strong phase difference in a Dalitz plot bin labelled by i, respectively. These quantities have been obtained for D → KSπ+π− (and D → KSK+K−) by CLEOc (see also here). Results on these quantities for D → KSπ+π− have also been published by BESIII (see also here), who have also produced results on the relevant quantities for D → KSK+K− here)
Model-independent determinations of γ ≡ φ3 from B− → D K− with D → KSπ+π− and D → KSK+K− decays have been performed by LHCb and from a combined analysis of Belle and Belle II data. The latter analysis supersedes a previous measurement by Belle. The variables (x±, y±), defined above are determined from the data. In both analyses the B− → D π− mode with the same D decays is also fit simultaneously. This provides for control of some sources of potential systematic uncertainty, and also allows additional parameters, denoted xξ and yξ (following the proposal of Garra Tico et al.) to be determined from the data. Since these additional parameters do not have significant sensitivity to γ ≡ φ3, we do not list them here and do not include them in the global combination. However, this parameterisation does mean that the small amount of sensitivity to γ from the B− → D π− modes is included in the x±, y± observables.
Belle have also performed a model-independent determination of γ ≡ φ3 using B− → D K− with D → KSπ+π−π0 decays. This relies on hadronic parameters of the D decay determined by CLEO-c data. The B− → D π− decays with the same charm final state are also studied, but since the parameters of this decay have little sensitivity to γ ≡ φ3 they are not listed here. The (x±, y±) variables determined in this analysis are the same as those determined with D → KSπ+π− and D → KSK+K− decays, but the averages are performed separately for convenience.
LHCb have performed a similar analysis of B−→DK− with D→K+K−π+π−. However, there are currently no measurements of the ci and si parameters available. Instead, values obtained from a model are used, with uncertainties corresponding to those expected in the BESIII data sample. It is anticipated that these measurements will be updated to be fully model-independent once determinations of ci and si from quantum-correlated D decays become available.
LHCb have also studied B−→D*K− with D→KSh+h− (h = π or K). Two measurements are available, one in which the D*→Dπ0 and Dγ decays are fully reconstructed and another in which a partial reconstruction technique is used. Although these two measurements come from the same data sample, the correlations between them have been determined to be small, and therefore they can be combined.
The results below have three sets of errors, which are statistical, systematic, and uncertainty coming from the knowledge of ci and si respectively. To perform the average, we remove the last uncertainty, which should be strongly correlated between the measurements. Since the size of the uncertainty from ci and si is found to depend on the size of the B → DK data sample, we assign the LHCb uncertainties (which are the smaller of the Belle and LHCb values) to the averaged result. This procedure should be conservative.
| Mode | Experiment | x+ | y+ | x- | y- | Correlation | Reference | |
|---|---|---|---|---|---|---|---|---|
|
DK−
D→KSh+h− |
Belle & Belle II ∫Ldt=(711+128) fb−1 |
−0.113 ± 0.032 ± 0.002 ± 0.002 | −0.046 ± 0.042 ± 0.001 ± 0.006 | 0.092 ± 0.033 ± 0.002 ± 0.002 | 0.100 ± 0.042 ± 0.002 ± 0.007 | (stat), (syst), (extra) | JHEP 2202 (2022) 063 | |
|
LHCb
∫Ldt=9 fb−1 |
−0.093 ± 0.010 ± 0.002 ± 0.002 | −0.013 ± 0.012 ± 0.003 ± 0.003 | 0.057 ± 0.010 ± 0.002 ± 0.002 | 0.066 ± 0.011 ± 0.003 ± 0.004 | (stat), (syst), (extra) | JHEP 2102 (2021) 169 | ||
| Average (*) | −0.094 ± 0.010 | −0.015 ± 0.012 | 0.060 ± 0.009 | 0.068 ± 0.011 | (stat) |
HFLAV correlated average
χ2 = 2.9/4 dof (CL=0.58 ⇒ 0.6σ) |
||
|
|

eps.gz png |

eps.gz png |
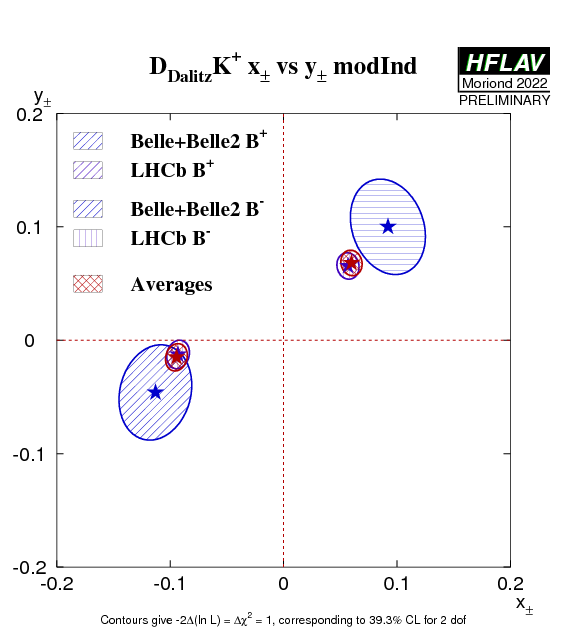
eps.gz png |
. | ||||
|
DK−
D→KSπ+π−π0 |
Belle
N(BB)=772M |
−0.030 ± 0.121 +0.017 −0.018 +0.019 −0.018 | 0.220 +0.182 −0.541 ± 0.032 +0.072 −0.071 | 0.095 ± 0.121 +0.017 −0.016 +0.023 −0.025 | 0.354 +0.144 −0.197 +0.015 −0.021 +0.032 −0.049 | (stat) | JHEP 1910 (2019) 178 | |
|
DK−
D→K+K−π+π− |
LHCb (**)
∫Ldt=9 fb−1 |
0.079 ± 0.029 ± 0.004 ± 0.004 | −0.033 ± 0.034 ± 0.004 ± 0.036 | −0.125 ± 0.025 ± 0.003 ± 0.017 | −0.042 ± 0.031 ± 0.003 ± 0.013 | (stat) (syst) | EPJ C83 (2023) 547 | |
|
D*K−
D→KSh+h− |
LHCb full rec
∫Ldt=9 fb−1 |
0.114 ± 0.032 ± 0.013 ± 0.004 | −0.089 ± 0.035 ± 0.020 ± 0.002 | 0.036 ± 0.044 ± 0.021 ± 0.003 | −0.168 ± 0.040 ± 0.015 ± 0.006 | (stat) (syst) (extra) | JHEP 2312 (2023) 013 | |
|
LHCb part rec
∫Ldt=9 fb−1 |
0.060 ± 0.026 ± 0.009 ± 0.002 | −0.063 ± 0.029 ± 0.011 ± 0.006 | 0.054 ± 0.029 ± 0.009 ± 0.004 | −0.048 ± 0.057 ± 0.014 ± 0.015 | (stat) (syst) (extra) | JHEP 2402 (2024) 118 | ||
| Average (*) (***) | 0.078 ± 0.021 | −0.082 ± 0.023 | 0.042 ± 0.025 | −0.125 ± 0.033 | (stat) |
HFLAV correlated average
χ2 = 4.4/4 dof (CL=0.35 ⇒ 0.9σ) |
||
|
|
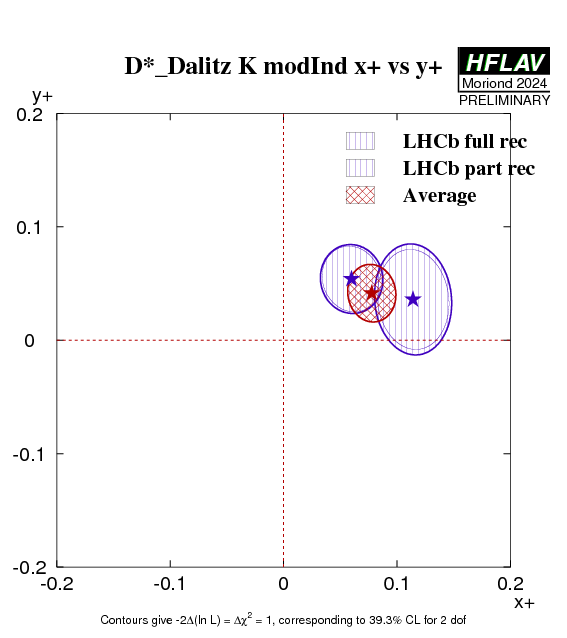
eps.gz png |
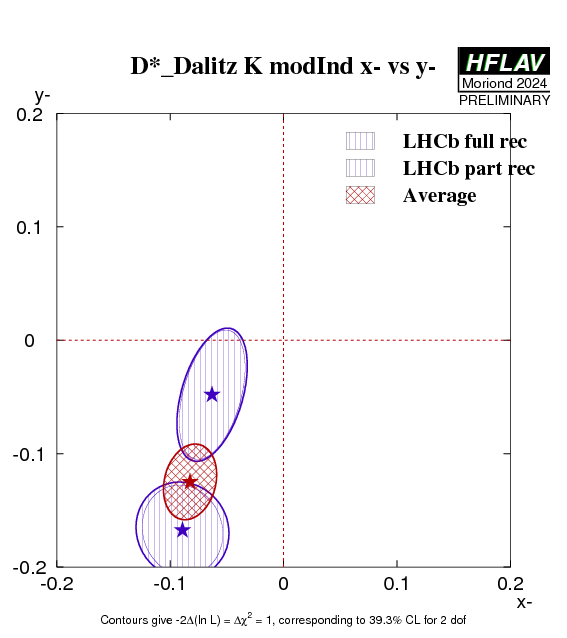
eps.gz png |
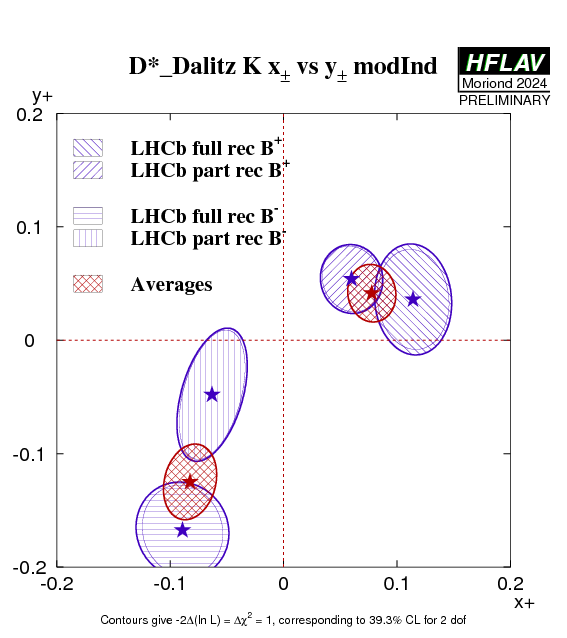
eps.gz png |
. | ||||
(*) Averages are performed without the uncertainty due to limited knowledge of the hadronic ci and si parameters, which should be strongly correlated between the measurements.
(**) These measurements are not model-independent since the values of the ci and si hadronic parameters are taken from a model. Note also that results from an unbinned analysis of B−→DKKππK− based on the same data sample are reported above.
(***) Correlations between the measurements with fully and partially reconstruced final states are neglected.
|
Compilation of (x±,y±) measurements from model-independent B → D(*)K(*) decays with multibody self-conjugate D decays. NB. The uncertainities in these plots do not include model errors. |

eps.gz png |

eps.gz png |
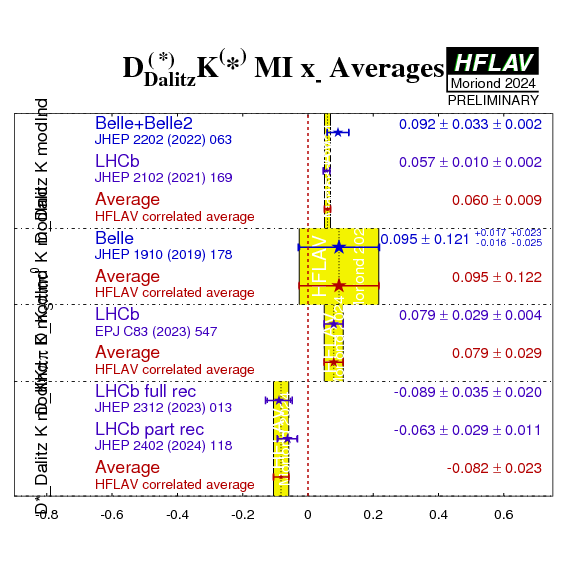
eps.gz png |
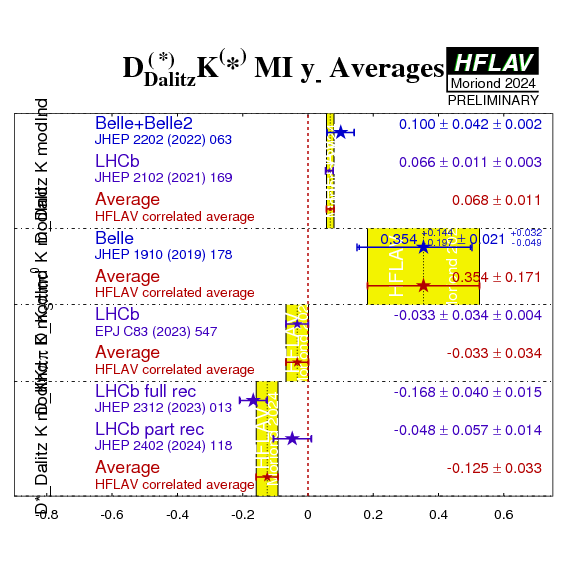
eps.gz png |
Digression:
|
Constraining γ ≡ φ3:
As above, the measurements of x+,− and y+,− can be used to place bounds on γ ≡ φ3. Belle and LHCb have done so, using B− → D K− with D → KSπ+π− decays, using a frequentist technique. |
|||
|
Belle and Belle II obtain
φ3 = (78.4 ± 11.4 ± 0.5 ± 1.0)° |
LHCb obtain
γ = (68.7 +5.2−5.1)° |
||
| rB (DK−) = 0.129 ± 0.024 ± 0.001 ± 0.002 | δB (DK−) = (124.8 ± 12.9 ± 0.5 ± 1.7)° | rB (DK−) = 0.0904 +0.0077−0.0075 | δB (DK−) = (118.3 +5.5−5.6)° |
| Belle have made a similar interpretation of their results from B− → DK− with D → KSπ+π−π0 decays, obtaining a 95% confidence level interval of [−29.7°,109.5°] on γ ≡ φ3. Combining the model-independent results from B− → DK− with D → KSπ+π−π0 decays with those from B− → DK− and B0 → DK*0 with D → KSπ+π− decays, Belle obtain φ3 = (74 +13−14)°. | |||
| From the LHCb analysis of B−→DK− with D→K+K−π+π− decays, the following constraints are set: γ = (116 +12−14)°, rB (DK−) = 0.110 ± 0.020, δB (DK−) = (81 +14−13)° | |||
|
For B−→D*K− with D→KSh+h− decays, the following constraints are available: LHCb full rec γ = (69 +13−14)°, rB (D*K−) = 0.15 ± 0.03, δB (D*K−) = (311 ±14)° LHCb part rec γ = (92 +21−17)°, rB (D*K−) = 0.080 +0.022−0.023 δB (D*K−) = (310 +15−20)° |
|||
| Note that the above results suffer an ambiguity: γ → γ + π ≡ φ3 → φ3 + π, δ → δ + π. We quote the result which is consistent with the Standard Model fit. | |||
Decays of D mesons to KSK+−π−+ can be used in a similar approach to that discussed above to determine γ ≡ φ3. Since these decays are less abundant, the event samples available to date have not been sufficient for a fine binning of the Dalitz plots, but the analysis can be performed using only an overall coherence factor and related strong phase difference for the decay. These quantities have been determined by CLEO both for the full Dalitz plots and in a restricted region ±100 MeV/c2 around the peak of the K*(892)± resonance.
LHCb have reported results of an analysis of B− → D K− and B− → D π− decays with D → KSK+−π−+. The decays with different final states of the D meson are distinguished by the charge of the kaon from the decay of the D meson relative to the charge of the B meson, and are labelled "same sign" (SS) and "opposite sign" (OS). Six observables potentially sensitive to γ ≡ φ3 are measured: two ratios of rates for DK and Dπ decays (one each for SS and OS) and four asymmetries (for DK & Dπ, SS & OS). This is done both for the K*(892)±-dominated region (with the same boundaries as used by CLEO), and for the remainder of the Dalitz plot. The results do not yet have sufficient precision to set significant constraints on γ ≡ φ3 independently of other results.
| Mode | Experiment | ASS,Dπ | AOS,Dπ | ASS,DK | AOS,DK | RSS | ROS | Correlations | Reference |
|---|---|---|---|---|---|---|---|---|---|
|
DK−
D→K*(892)+−K−+ |
LHCb
∫Ldt=9 fb−1 |
−0.020 ± 0.011 ± 0.003 | 0.007 ± 0.017 ± 0.003 | 0.084 ± 0.049 ± 0.008 | 0.021 ± 0.094 ± 0.017 | 0.079 ± 0.004 ± 0.002 | 0.062 ± 0.006 ± 0.003 | (stat) (syst) | JHEP 2006 (2020) 058 |
|
Belle + Belle II
N(BB)=1159M |
0.046 ± 0.029 ± 0.016 | 0.009 ± 0.046 ± 0.009 | 0.055 ± 0.119 ± 0.020 | 0.231 ± 0.184 ± 0.014 | 0.093 ± 0.012 ± 0.005 | 0.103 ± 0.020 ± 0.006 | (stat) (syst) | JHEP 09 (2023) 146 | |
| Average | −0.013 ± 0.011 | 0.007 ± 0.016 | 0.081 ± 0.046 | 0.066 ± 0.085 | 0.080 ± 0.004 | 0.066 ± 0.006 | (stat) |
HFLAV correlated average
χ2 = 8.9/6 dof (CL=0.18 ⇒ 1.3σ) |
|
|
DK−
D→KSK+−π−+ (non-K*) |
LHCb
∫Ldt=9 fb−1 |
−0.034 ± 0.020 ± 0.003 | 0.003 ± 0.015 ± 0.003 | 0.095 ± 0.089 ± 0.018 | −0.038 ± 0.075 ± 0.011 | 0.081 ± 0.008 ± 0.004 | 0.073 ± 0.006 ± 0.002 | (stat), (syst) | JHEP 2006 (2020) 058 |
|
DK−
D→KSK+−π−+ (all) |
Belle + Belle II
N(BB)=1159M |
0.018 ± 0.026 ± 0.009 | −0.028 ± 0.031 ± 0.009 | −0.089 ± 0.091 ± 0.011 | 0.109 ± 0.133 ± 0.013 | 0.122 ± 0.012 ± 0.004 | 0.093 ± 0.013 ± 0.003 | (stat) (syst) | JHEP 09 (2023) 146 |
LHCb have presented results on B0 → DK*0 with the GLW modes D → K+K− and π+π−, the GLW-like mode D → π+π−π+π−, and the ADS modes D → K+π− and K+π−π+π−. The sensitivity to γ ≡ φ3 arises in the same way as discussed above, except that the magnitude of the ratio of amplitudes rB is expected to be larger, ≈ 0.3, because both amplitudes are colour-suppressed. Effects due to the natural width of the K*0 are handled in a quasi-two-body approximation using the parametrization suggested by Gronau, whereby an additional parameter κ, referred to as a coherence factor, is introduced. In addition, the hadronic factors rB and δB are replaced by effective parameters rB and δB. These parameters depend on the K*0 selection window used; all analyses make very similar requirements (the emerging consensus is to use m(K+π−) within 50 MeV/c2 of the K*(892)0 pole mass and helicity angle satisfying |cos(θK*0)|>0.4).
| Mode | Experiment | ACP+ | RCP+ | Correlation | Reference |
|---|---|---|---|---|---|
| DCPK*0 |
LHCb KK
∫Ldt=9 fb−1 |
−0.047 ± 0.063 ± 0.015 | 0.811 ± 0.057 ± 0.017 | 0.040 (stat) −0.030 (syst) | JHEP 05 (2024) 025 |
|
LHCb pipi
∫Ldt=9 fb−1 |
−0.034 ± 0.094 ± 0.016 | 1.104 ± 0.111 ± 0.026 | 0.040 (stat) −0.030 (syst) | JHEP 05 (2024) 025 | |
| Mode | Experiment | A_GLW | R_GLW | Correlation | Reference |
| DππππK*0 |
LHCb
∫Ldt=9 fb−1 |
0.021 ± 0.087 ± 0.016 | 0.882 ± 0.086 ± 0.033 | 0.000 (stat) −0.030 (syst) | JHEP 05 (2024) 025 |
| Mode | Experiment | R+ | R− | Correlation | Reference |
| DKπK*0 |
LHCb
∫Ldt=9 fb−1 |
0.069 ± 0.013 ± 0.005 | 0.093 ± 0.013 ± 0.005 | 0.060 (stat) 0.150 (syst) | JHEP 05 (2024) 025 |
| DKπππK*0 |
LHCb
∫Ldt=9 fb−1 |
0.060 ± 0.014 ± 0.006 | 0.038 ± 0.014 ± 0.006 | 0.080 (stat) −0.010 (syst) | JHEP 05 (2024) 025 |
Digression:
|
We do not include older results from BaBar and Belle where no significant signal was observed and a different parametrisation was used.
Combining the results and using additional input from CLEOc (here and here), Taking external input for hadronic parameters, LHCb obtain r<sub>B(DK*0) = 0.235 ± 0.017, as well as obtaining constraints in the space of (γ, rB(DK*0), δB(DK*0)). |
As pointed out by Gershon (see also Gershon and Williams), a Dalitz plot analysis of B0 → DK+π− decays provides more sensitivity to γ than the quasi-two-body DK*0 approach. The analysis provides direct sensitivity to the hadronic parameters rB and δB associated with the B0 → DK*0 decay amplitudes, rather than effective hadronic parameters averaged over the K*0 selection window as in the quasi-two-body case. The results of the analysis can be presented in terms of Cartesian parameters, as done for the BPGGSZ analysis, or alternatively directly in terms of γ, rB and δB.
Such an analysis has been performed by LHCb. A simultaneous fit is performed to the B0 → DK+π− Dalitz plots with the neutral D meson reconstructed in the K+π−, K+K− and π+π− final states. The reported results are for the parameters associated with the B0 → DK*(892)0 decay.
| Experiment | x+ | y+ | x− | y− | Correlation | Reference |
|---|---|---|---|---|---|---|
|
LHCb
∫Ldt=3 fb−1 |
0.04 ± 0.16 ± 0.11 | −0.47 ± 0.28 ± 0.22 | −0.02 ± 0.13 ± 0.14 | −0.35 ± 0.26 ± 0.41 | (stat) (syst) | PR D93 (2016) 112018 |
Note that, since the measurements use overlapping data samples, these results cannot be combined with the LHCb results for GLW observables in B0 → DK*0 decays reported above.
Digression:
| LHCb use these results to obtain confidence levels for γ, rB(DK*0) and δB(DK*0). In addition, results are reported for the hadronic parameters needed to relate these results to quasi-two-body measurements of B0 → DK*0 decays, where a selection window of m(K+π−) within 50 MeV/c2 of the pole mass and helicity angle satisfying |cos(θK*0)|>0.4 is assumed. These parameters are the coherence factor κ, the ratio of quasi-two-body and amplitude level rB values, RB = rB/rB, and the difference between quasi-two-body and amplitude level δB values, ΔδB = δB−δB. | |
| LHCb obtain κ = 0.958 +0.005−0.010 +0.002−0.045, RB = 1.02 +0.03−0.01 ±0.06, ΔδB = 0.02 +0.03−0.02 ±0.11 | |
As discussed above for B− → DK−, Dalitz plot analysis of a three-body D decay allows simultaneous determination of the weak phase difference γ ≡ φ3, the strong phase difference δB and the ratio of amplitudes rB. In order to avoid complications due to B0–B0 oscillations (see here), the decay to the self-tagging final state DK*0, with K*0 → K+π−, is used. Effects due to the natural width of the K*0 are accommodated through the coherence factor κ, and the effective hadronic factors rB and δB, as discussed above. Results obtained with both model-dependent and model-independent approaches are available. Note that due to the strong statistical and systematic correlations, model-dependent results and model-independent results from the same experiment cannot be combined.
BaBar have performed a similar model-dependent Dalitz plot analysis to that described above using neutral B decays, presenting results in terms of γ ≡ φ3 only. LHCb have done a similar analysis, using B0 → DK*0 with D → KSπ+π− decays, and presented results in terms of the Cartesian parameters. The third uncertainty in the results is due to model dependence.
| Experiment | x− | y− | x+ | y+ | Correlation | Reference |
|---|---|---|---|---|---|---|
|
LHCb
∫Ldt=3 fb−1 |
−0.15 ± 0.14 ± 0.03 ± 0.01 | 0.25 ± 0.15 ± 0.06 ± 0.01 | 0.05 ± 0.24 ± 0.04 ± 0.01 | −0.65 +0.24 −0.23 ± 0.08 ± 0.01 | (stat) | JHEP 1608 (2016) 137 |
Digression:
|
Constraining γ ≡ φ3:
BaBar extract the three-dimensional likelihood for the parameters (γ, δB(DK*0), rB(DK*0)) and, combining with a separately measured PDF for rB(DK*0) (using a Bayesian technique), obtain bounds on each of the three parameters. LHCb convert their results on the Cartesian parameters into bounds on γ, δB(DK*0) and rB(DK*0) using similar techniques to those discussed above. |
| BaBar obtain γ = (162 ± 56)°, δB(DK*0) = (62 ± 57)°, rB(DK*0) < 0.55 at 95% probability |
| LHCb obtain γ = (80 +21−22)°, δB(DK*0) = (197 +24−20)°, rB(DK*0) = 0.39 ± 0.13 |
| Note that there is an ambiguity in the solutions for γ and δB (γ, δB → γ+π, δB+π). |
Belle and LHCb have performed similar model-independent Dalitz plot analyses to those described above, but using B0 → DK*0 decays. Both experiments used D → KSπ+π− decays, and LHCb also included their D → KSK+K− sample. Results are presented in terms of the so-called Cartesian parameters. Belle give separately the uncertainties due to imperfect knowledge of the ci and si parameters obtained by CLEOc while LHCb constrain these parameters within uncertainties in the fit to data, and hence the effect is absorbed in their statistical uncertainties.
| Experiment | x+ | y+ | x− | y− | Correlation | Reference |
|---|---|---|---|---|---|---|
|
Belle
N(BB)=772M |
0.1 +0.7 −0.4 +0.0 −0.1 ± 0.1 | 0.3 +0.5 −0.8 +0.0 −0.1 ± 0.1 | 0.4 +1.0 −0.6 +0.0 −0.1 ± 0.0 | −0.6 +0.8 −1.0 +0.1 −0.0 ± 0.1 | (stat) | PTEP 2016 043C01 |
|
LHCb
∫Ldt=9 fb−1 |
0.07 ± 0.09 ± 0.01 ± 0.01 | −0.34 ± 0.10 ± 0.02 ± 0.01 | −0.21 ± 0.09 ± 0.00 ± 0.01 | −0.01 ± 0.13 ± 0.02 ± 0.01 | (stat) (syst) (extra) | EPJ C84 (2024) 206 |
| Average | 0.08 ± 0.09 | −0.32 ± 0.11 | −0.21 ± 0.09 | −0.02 ± 0.13 | (stat) |
HFLAV correlated average
χ2 = 2.0/4 dof (CL=0.74 ⇒ 0.3σ) |
(*) Note that the Belle results have significantly non-Gaussian and asymmetric uncertainties, and therefore the averages and plots should be interpreted carefully.
Digression:
|
Constraining γ ≡ φ3:
From these results, Belle set the constraint rB(DK*0) < 0.87 at 68% confidence level. LHCb obtain constraints on γ, rB(DK*0) and δB(DK*0) using a frequentist technique. |
|||||
| γ = (49 +22−19)°, δB(DK*0) = (236 +19−21)°, rB(DK*0) = 0.271 +0.065−0.066 | |||||
| Note that there is an ambiguity in the solutions for γ and δB (γ, δB → γ+π, δB+π). | |||||
All ground-state b hadrons can in principle be used to measure observables sensitive to γ ≡ φ3 through the interference between b → cu-bar s & b → uc-bar s amplitudes. LHCb have made a first measurement using the Λb0 → DpK− mode with subsequent D → Kπ decays. The quantities measured are the ratio of rates to the favoured and suppressed final states, denoted R (this is equivalent to the inverse of RADS defined previously) and the asymmetry in the suppressed final state (equivalent to AADS defined previously). Due the multibody final state, the relations of these observables to γ ≡ φ3 involve an unknown coherence factor in a similar way as discussed for B0 → DK*0. Results are presented both in the full phase-space of the decay and in the restricted region M2(pK−) < 5 GeV2/c4, where larger CP violation effects are expected to be possible. As they involve overlapping data samples, these two results are correlated.
| Mode | Experiment | (RADS)−1 | AADS | Reference |
|---|---|---|---|---|
| DpK (full phase-space) |
LHCb
∫Ldt=9 fb−1 |
7.1 ± 0.8 +0.4 −0.3 | 0.12 ± 0.09 +0.02 −0.03 | PRD 104 (2021) 112008 |
| DpK (M2(pK−) < 5 GeV2/c4) |
LHCb
∫Ldt=9 fb−1 |
8.6 ± 1.5 +0.4 −0.3 | 0.01 ± 0.16 +0.03 −0.02 | PRD 104 (2021) 112008 |
BaBar and LHCb have presented constraints on γ ≡ φ3 from combinations of their results on B+ → DK+ and related processes.
(*) Belle presented in 2012 a preliminary combination of their results, but this remains unpublished after more than two years and therefore we do not list it.
|
BaBar obtain γ = (69 +17−16)° rB(DK+) = 0.092 +0.013−0.012 δB(DK+) = (105 +16−17)° rB(D*K+) = 0.0106 +0.019−0.036 δB(D*K+) = (294 +21−31)° rB(DK*+) = 0.143 +0.048−0.049 (*) δB(DK*+) = (101 ± 43)° (*) PRD 87 (2013) 052015 . . . . . . . . . |
LHCb obtain γ = (67 ± 4)° rB(DK+) = 0.0989 ±0.0050 δB(DK+) = (131.2 +5.1−5.9)° rB(D*K+) = 0.191 +0.045−0.038 δB(D*K+) = (332 +8−10)° rB(DK*+) = 0.092 +0.018−0.033 δB(DK*+) = (40 +92−20)° rB(DK*0) = 0.221 +0.044−0.047 δB(DK*0) = (187 +21−23)° rB(DKππ) = 0.081 +0.025−0.027 δB(DKππ) = (351 +9−37)° rB(DsK) = 0.30 ±0.09 δB(DsK) = (355 +17−16)° δB(Dπ) = (17 +29−17)° LHCb-CONF-2018-002, LHCb-CONF-2020-003 |
(*) The BaBar results presented here for rB(DK*+) and δB(DK*+) are those for κrs and δs in the publication
Independently from the constraints on γ ≡ φ3 obtained by the experiments, the results summarised above are statistically combined to produce world average constraints on γ ≡ φ3 and the hadronic parameters involved. The combination is performed with the GammaCombo framework and follows a frequentist procedure, similar to those used by the experiments.
The input measurements used in the combination are those listed above. Individual measurements are used as inputs, rather than the HFLAV averages, in order to facilitate cross-checks and to ensure the most appropriate treatment of correlations. A combination based on the HFLAV averages for each of the quantities measured by experiments gives consistent results.
In certain measurements, the experiments have explored different approaches to analysing the same data sample, and therefore choices of which results in include are needed. Concerning results of BPGGSZ analyses of B− → D(*) K(*)− decays, the model-dependent results from the BaBar and Belle experiments are used, whilst the model-independent results are used for LHCb. This choice is made in order to maintain consistency of the approach across experiments whilst maximising the size of the samples used to obtain inputs for the combination. For BPGGSZ analysis of B0 → DK*0 the model-independent result from LHCb is used for consistency. The LHCb results from the GLW analysis of B0 → DK*0 are not used because of the overlap with the GLW-Dalitz analysis which is used instead. Results from time-dependent analyses of Bd → D+−π−+, Bd → D*+−π−+ and Bd → D+−ρ−+ are not used as there are insufficient constraints on the associated hadronic parameters. Similarly, results from Bd → D+−KSπ−+ are not used.
Auxiliary inputs are used in the combination in order to constrain the D system parameters and subsequently improve the determination of γ ≡ φ3. These include the ratio of suppressed to favoured decay amplitudes and the strong phase difference for D → K+−π−+ decays, taken from the HFLAV Charm Physics subgroup global fits. The amplitude ratios, strong phase differences and coherence factors of D→K+−π−+π0, D→K+−π−+π+π− and D→KSK+−π+− decays are taken from CLEO-c and LHCb measurements. The fraction of CP-even content for quasi-GLW D→π+π−π+π−, D→K+K−π0 and D→π+π−π0 decays are taken from CLEO-c measurements. Constraints required to relate the hadronic parameters of the B0 → DK*0 GLW-Dalitz analysis to the effective hadronic parameters of the quasi-two-body approaches are taken from LHCb measurements. Finally, the value of −2βs is taken from the HFLAV Lifetimes and Oscillations subgroup; this is required to obtain sensitivity to γ ≡ φ3 from the time-dependent analysis of B0s → D−+sK+− decays decays.
The following reasonable, although imperfect, assumptions are made when performing the averages.
The obtained world averages for the Unitarity Triangle angle γ ≡ φ3 and related hadronic parameters are
The fit has a χ2 of 161.42 with 178 observables and 36 parameters. Using the χ2 distribution, this corresponds to a p-value of 12.7% (or 1.5σ). A coverage check with pseudoexperiments gives a p-value of (11.8 ± 0.3)%.
An ambiguous solution also exists at γ ≡ φ3 ⇔ γ + π ≡ φ3 + π (all strong phases δ are also simultaneously shifted by π).
There are two overlapping solutions for the B− → DK*− modes which is why their uncertainties are so asymmetric.
Figures:
| World average of γ ≡ φ3, in terms of 1−CL, split by decay mode. |

pdf png |
|
| World average of γ ≡ φ3, in terms of 1−CL, split by initial state. |
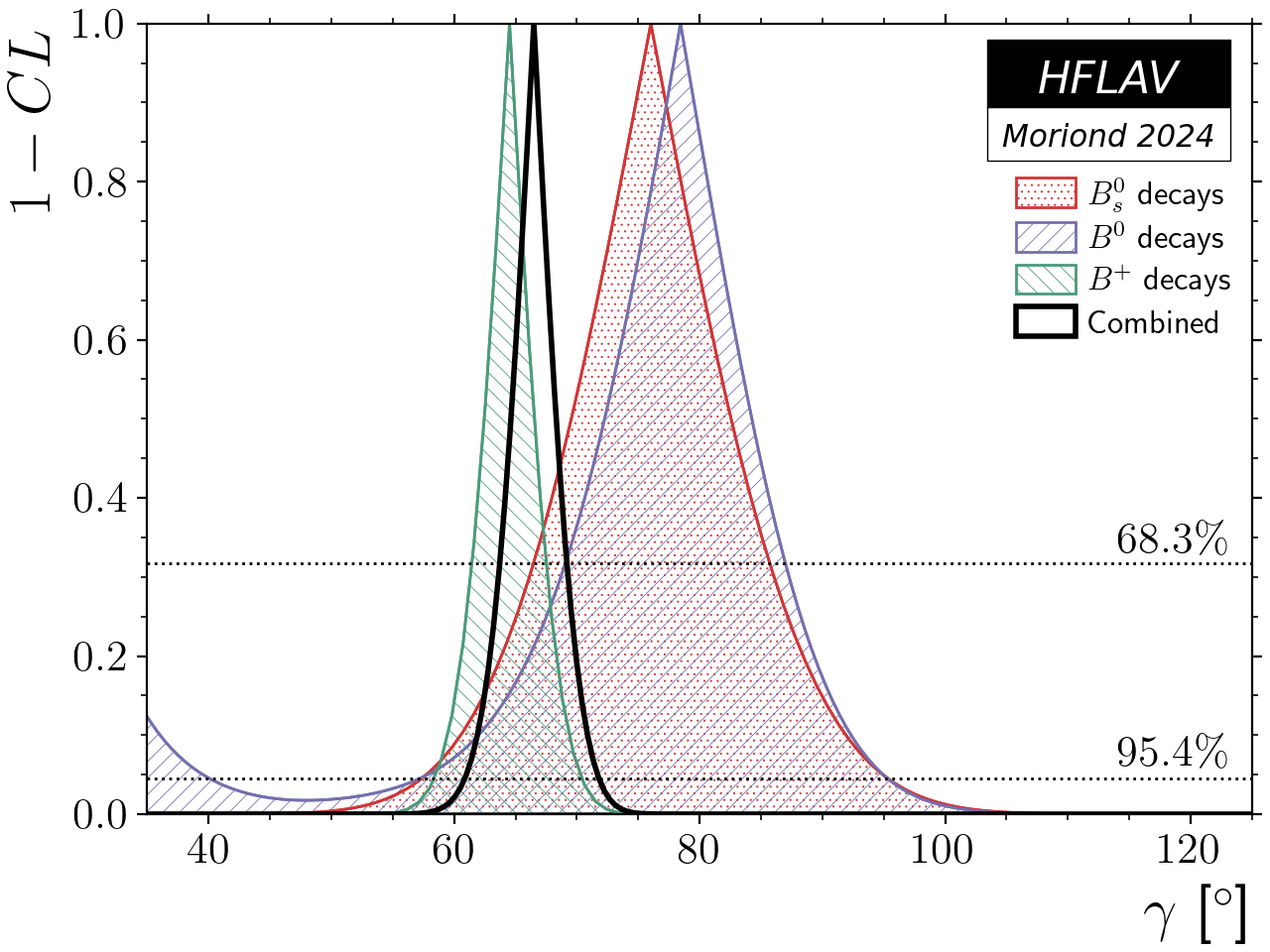
pdf png |
|
| World average of γ ≡ φ3, in terms of 1−CL, split by analysis method. |

pdf png |
|
| World averages for the hadronic parameters rB in the different decay modes, in terms of 1−CL. |
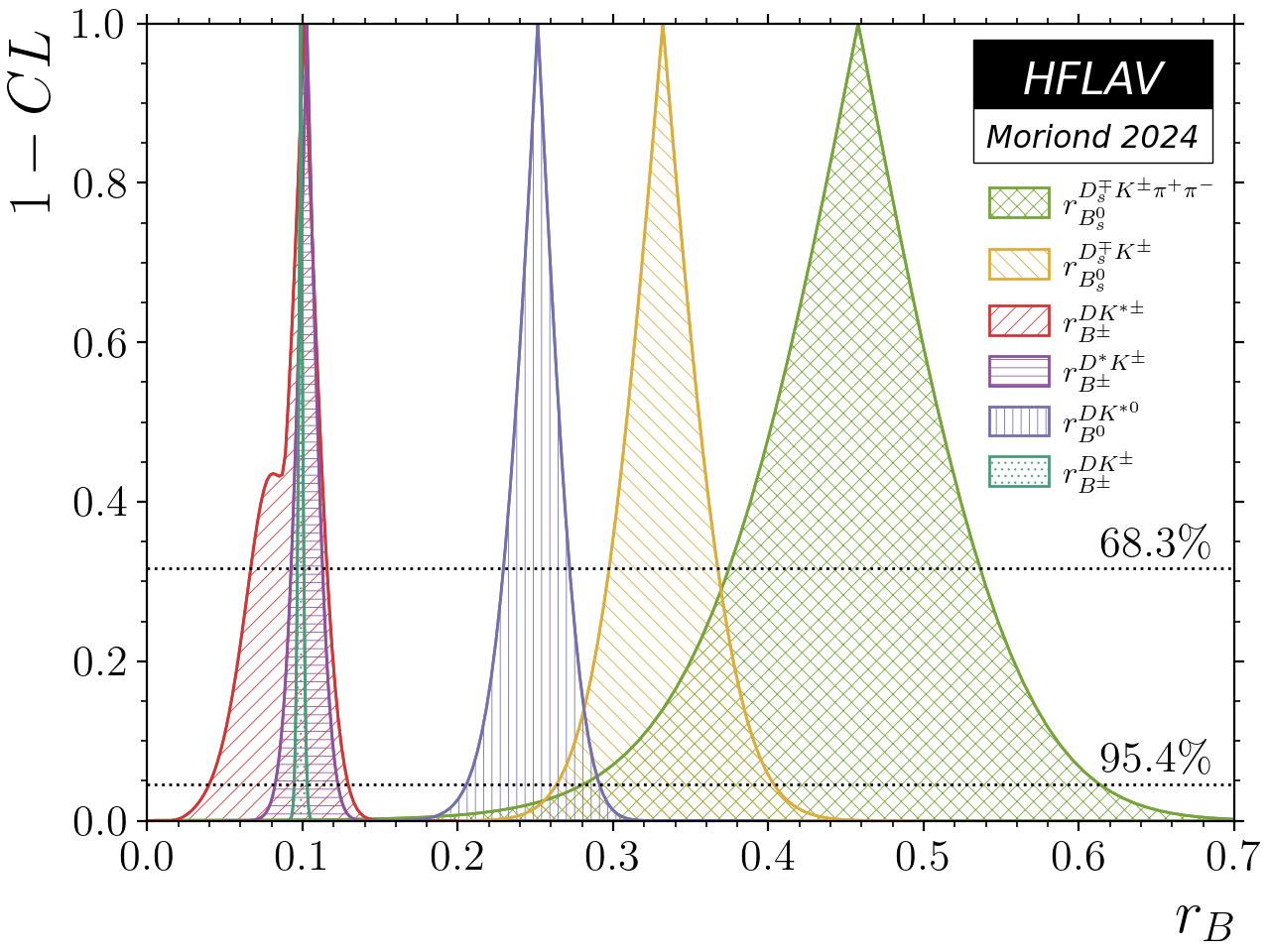
pdf png |
|
|
Contributions to the combination from different input measurements, shown in the plane of the relevant rB or δB parameter vs. γ ≡ φ3. Contours show the two-dimensional 68.3% and 95.4% CL regions. |
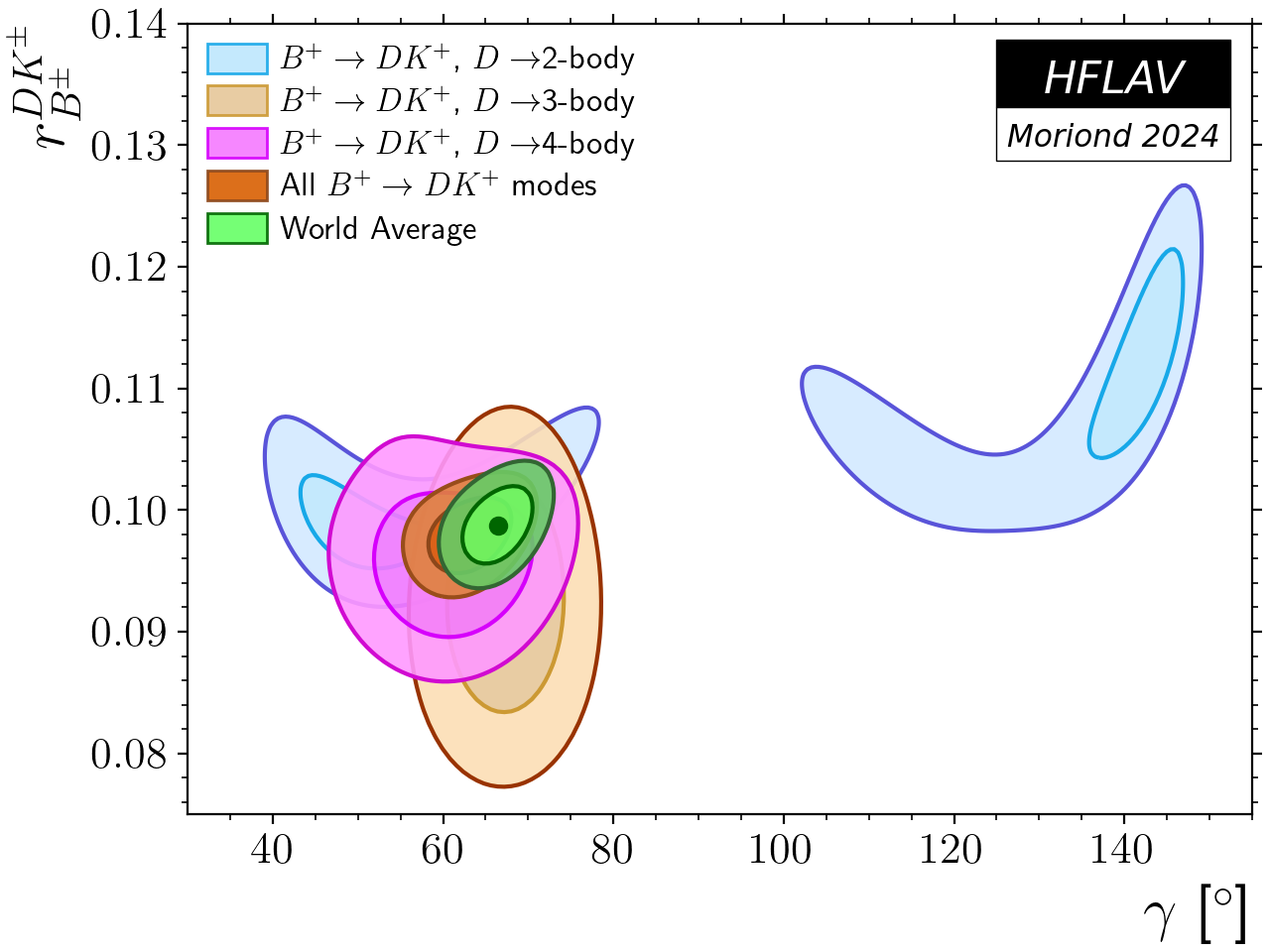
pdf png |

pdf png |
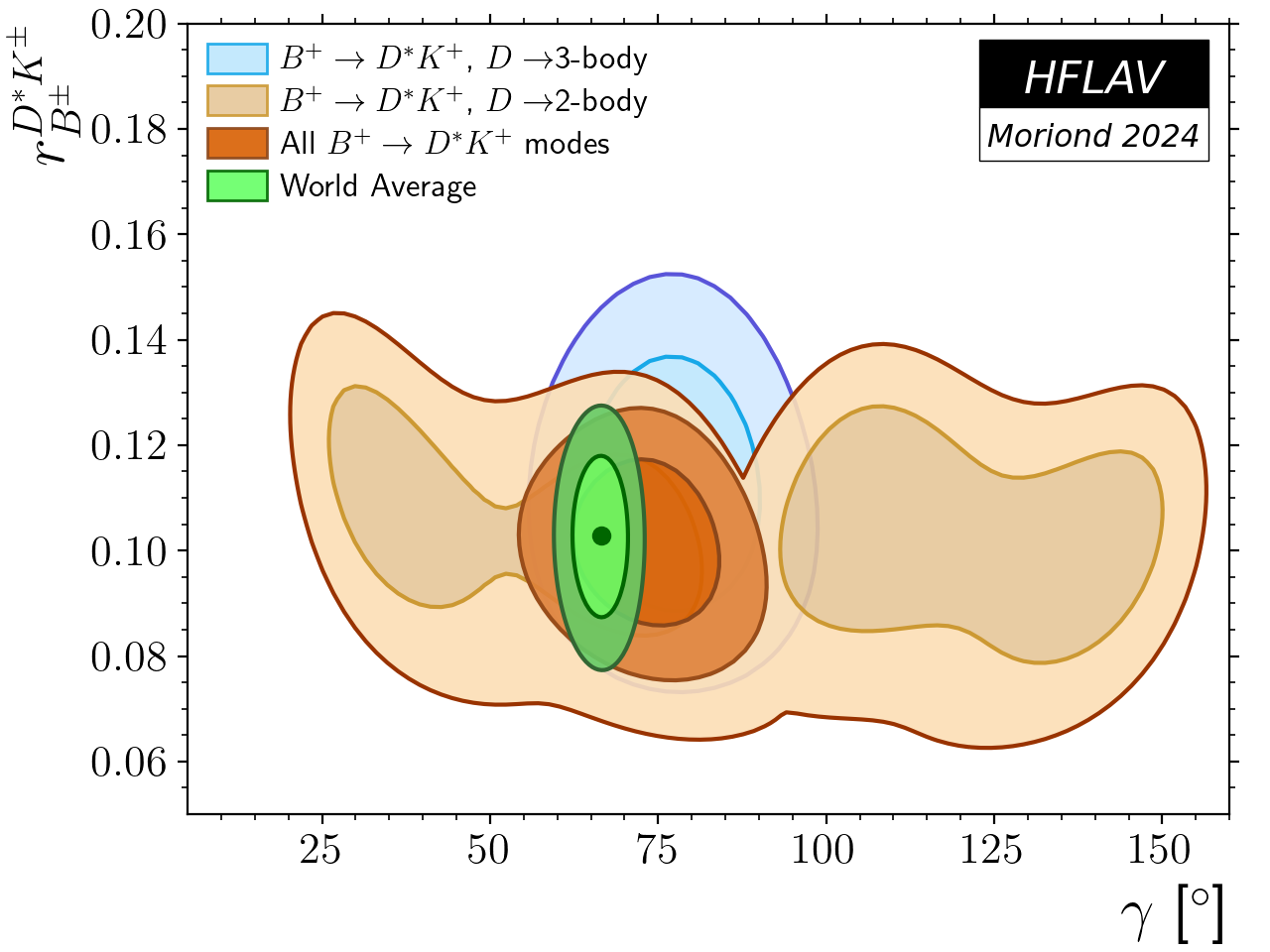
pdf png |

pdf png |
|

pdf png |
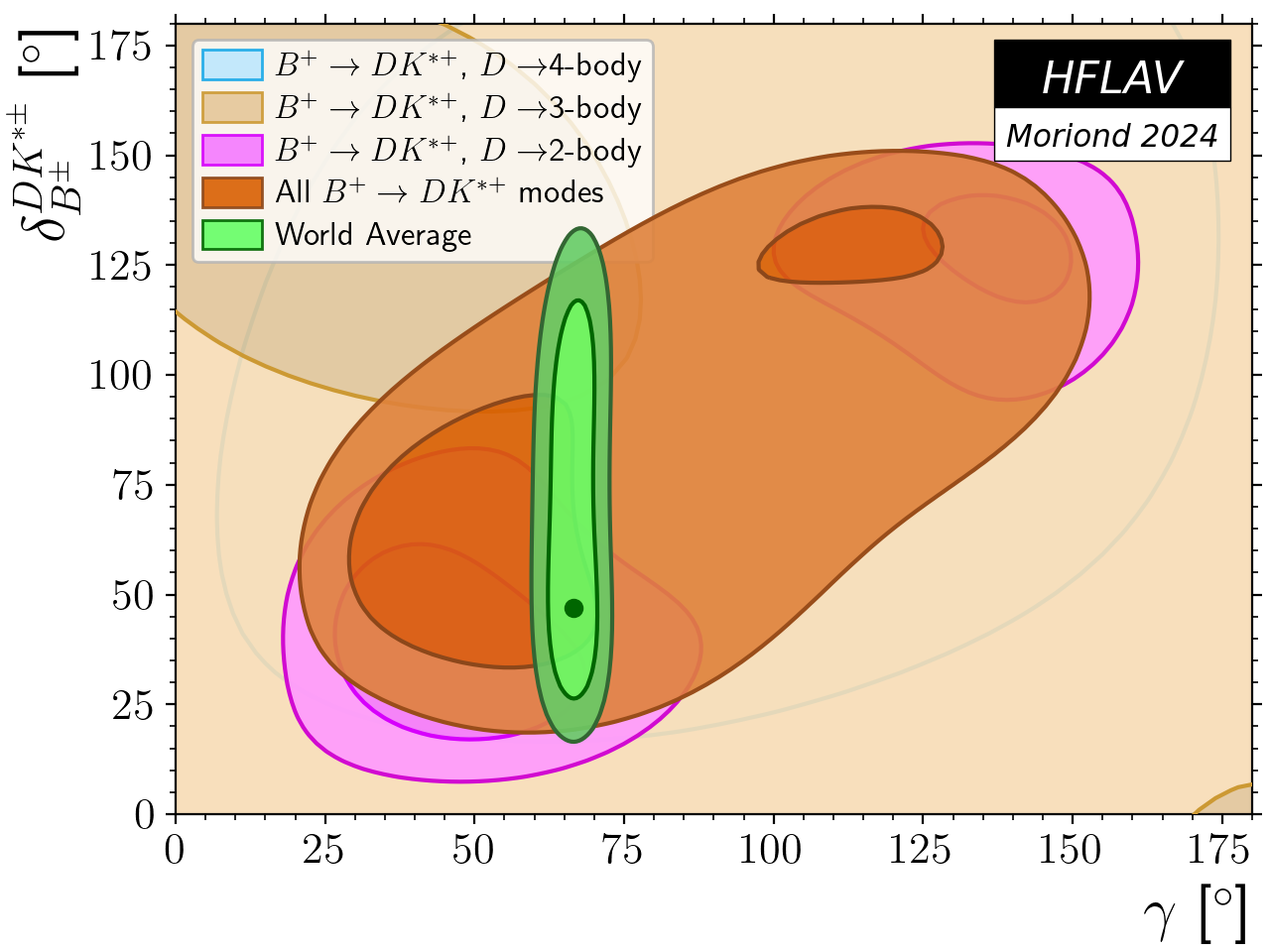
pdf png |
|
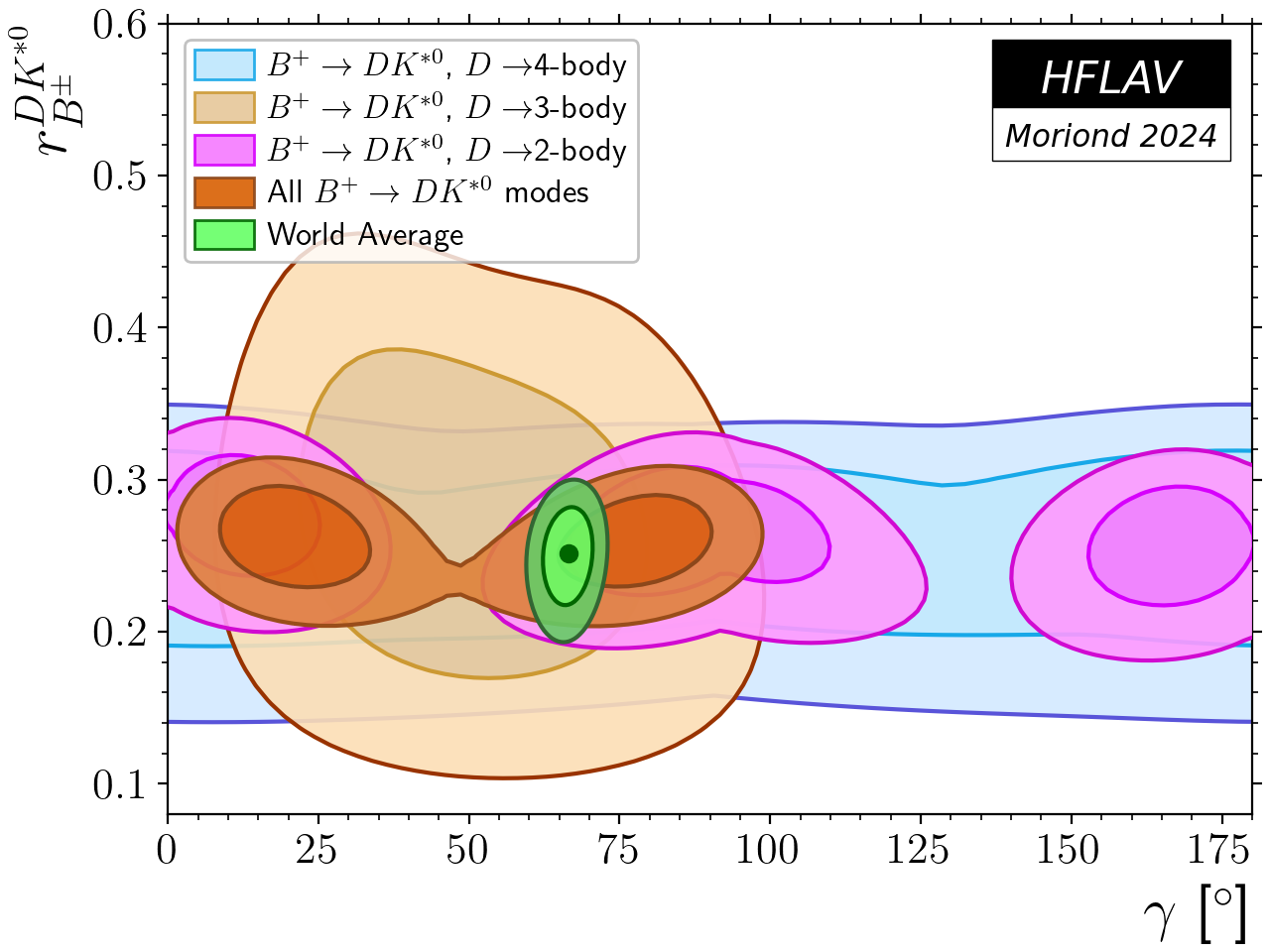
pdf png |
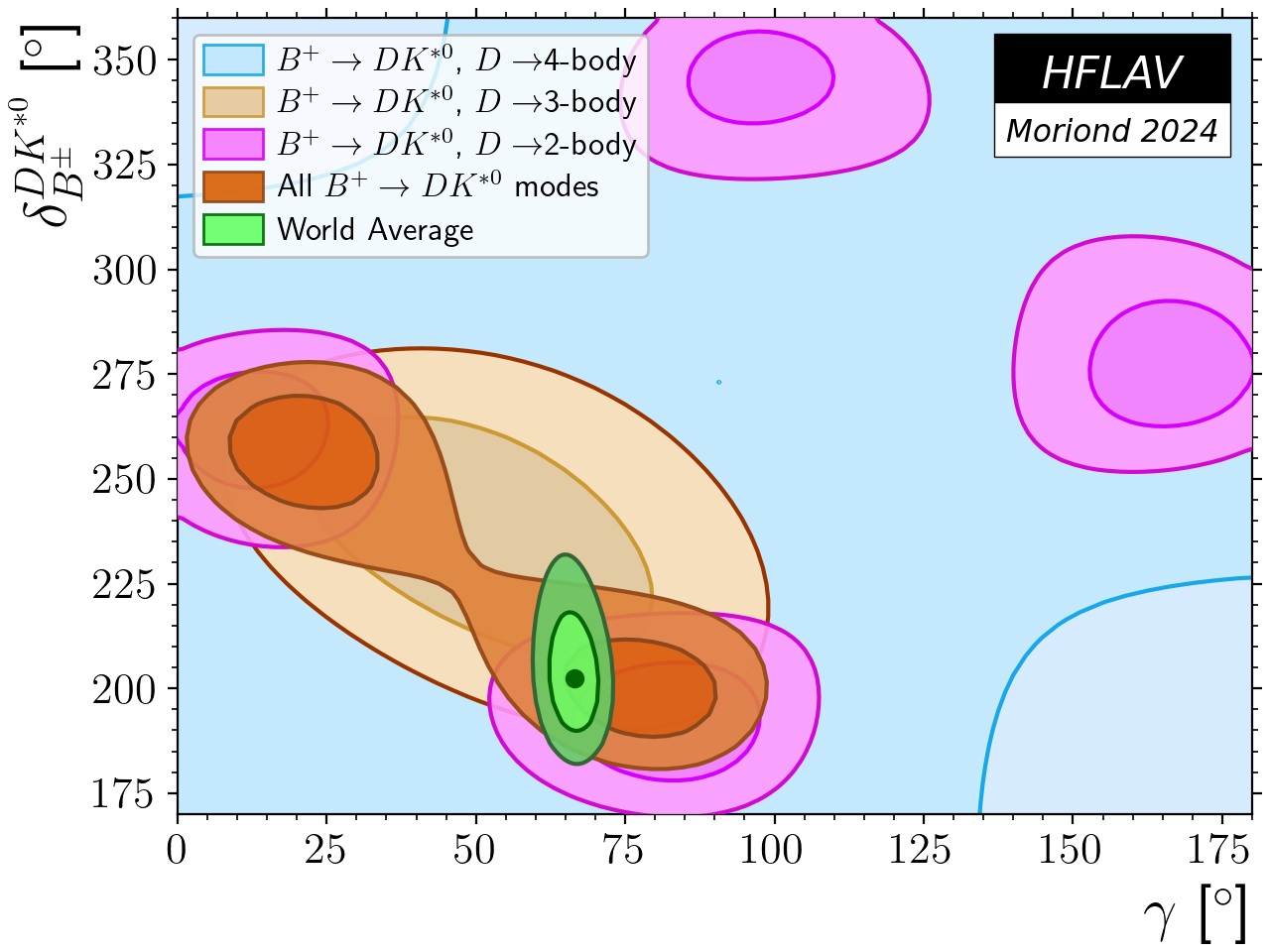
pdf png |
|
The plots below show the constraints, in the (ρ, η) plane on
Whether or not the three allowed areas overlap at a common point in the plane is a consistency test of the Standard Model. Similar plots including additional constraints, for example on the lengths of the sides of the Unitarity Triangle, can be found at the CKMfitter and UTfit pages.
The obtained world averages for the apex of the Unitarity Triangle are
Figures:
| World average constraints on the angles of the Unitarity Triangle, in the (ρ, η) plane. |

pdf png |
|