PDG 2024 averages

All results published before March 1, 2024 have been included in the averages computed by the lifetime and oscillations sub-group of the Heavy Flavour Averaging Group (HFLAV) for the 2024 edition of the Review of Particle Physics by the Particle Data Group. The following material is available: The combination procedure are described in Chapter 5 of the following HFLAV publication:

(home , top , next, previous )

b-hadron lifetime averages

The lifetimes displayed in the table below have been obtained by combining time-dependent measurements from ALEPH, ATLAS, BABAR, BELLE, CDF, CMS, D0, DELPHI, L3, LHCb, OPAL and SLD.

b-hadron species average lifetime lifetime ratio
B0 1.517 ± 0.004 ps
B+ 1.638 ± 0.004 ps B+/B0 = 1.076 ± 0.004
Bs0 1.520 ± 0.005 ps Bs0/B0 = 1.0032 ± 0.0032
BsL 1.429 ± 0.006 ps
BsH 1.622 ± 0.008 ps
Bc+ 0.510 ± 0.009 ps
Λb 1.471 ± 0.009 ps Λb/B0 = 0.969 ± 0.006
Ξb− 1.572 ± 0.040 ps
Ξb0 1.480 ± 0.030 ps Ξb0/Ξb− = 0.929 ± 0.028
Ωb− 1.64 +0.18 −0.17 ps Ωb−/B0 = 1.08 +0.12 −0.11

The above B0 lifetime average is obtained assuming there is no decay width difference in the B0 system. The above Bs lifetime is defined as 1/Γs, where Γs = (ΓL + ΓH)/2 is the mean decay width of the Bs system, i.e. the average of the decay widths of the light and heavy states (BsL and BsH). The Λb lifetime average is computed using only measurements with fully reconstructed hadronic decays; the measurements are slighlty discrepant (see plot), but no scale factor is applied on the combined error.

The tables below give a number of effective Bs lifetime averages, measured from single exponential fits of the proper time distributions of Bs decays to a number of interesting final states. In general each final state may be a different mixture of the two Bs mass eigenstates, and hence the effective lifetime falls somewhere between 1/ΓL and 1/ΓH. The "Bs → flavour specific" lifetime is measured mainly with Bs → Ds lepton X decays; it is used as input to extract the long and short lifetimes of the Bs system (see next section). The "Bs → J/ψ φ" lifetime is an average of the results from single exponential fits. Nowadays, the time dependence and the angular dependence of the Bs → J/ψ φ decays is analysed in a more sophisticated way in order to extract separately the long and short lifetimes (see further below). The Bs → μ+μ- effective lifetime is expected to be equal to the long lifetime in the Standard Model, but could be a mixture.

mixture of the two
Bs mass eigenstates 		effective lifetime from
single exponential fits
Bs → flavour specific 1.527 ± 0.011 ps
Bs → J/ψφ 1.480 ± 0.007 ps
Bs → μ+μ- 1.79 ± 0.17 ps

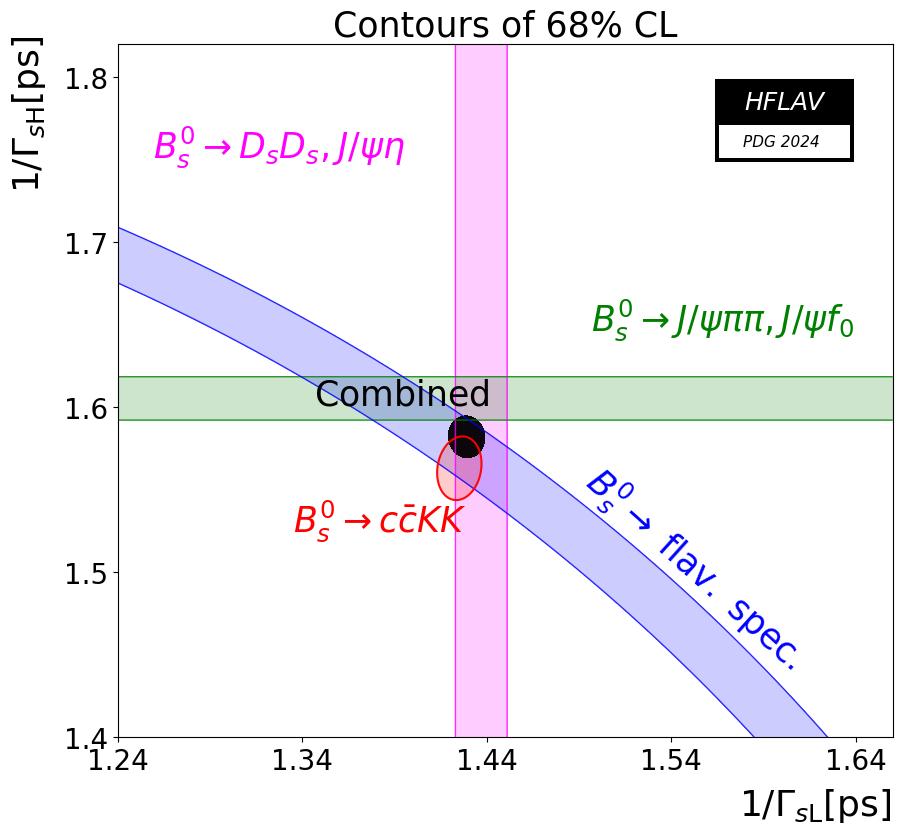
The two tables below report effective Bs lifetime averages for final states that are either pure CP-even or pure CP-odd eigenstates. If the corresponding Bs decays are dominated by a single weak phase and if CP violation can be neglected, then the effective lifetime for decays to CP-even (CP-odd) eigenstates corresponds to 1/ΓL (1/ΓH). These averages are used as constraints in the fit to determine Γs and ΔΓs (see further below).

CP-even final states effective lifetime from
single exponential fits
Bs →  J/ψη,   Ds+Ds− 1.437 ± 0.014 ps

CP-odd final states effective lifetime from
single exponential fits
Bs →  J/ψf0(980),   J/ψπ+π− 1.646 ± 0.013 ps


(home , top , next, previous)

Neutral B meson mixing: decay width differences

For both the B0 and Bs systems, the mean decay width and the decay width difference are defined here as ΔΓ = ΓL − ΓH and Γ = (ΓL + ΓH)/2, where ΓL (ΓH) is the decay width of the light (heavy) mass eigenstate. In the Standard Model, one expects ΔΓ > 0, i.e. the light (heavy) mass eigenstate is also the short-lived (long-lived) mass eigenstate. This expectation has been observed to be correct for the Bs system. In the absence of CP violation, the light (heavy) B0 or Bs mass eigenstate is the CP-even (CP-odd) eigenstate. This assumption is made by some analyses included in the combined results given in this section.

Combined result on the relative decay width difference in the B0 system:

s×ΔΓd/Γd = 0.001 ± 0.010 from DELPHI, BABAR, Belle, ATLAS, CMS and LHCb

The quantity s = sign(Re(λCP)), where λCP = (q/p)×ACP/ACP refers to a CP-even final state (e.g. J/ψKL), is predicted to be equal to s= +1 to a high degree of confidence from the Standard Model fits to all available constraints on the unitarity triangle.

The time-dependent and tagged angular analyses of the Bs → J/ψ φ decay by ATLAS, CMS, CDF and D0, as well as those of the Bs → J/ψKK and Bs → ψ(2S)φ decays by LHCb, provide information on Γs, ΔΓs and the weak phase φsccs, defined as the phase difference between the mixing amplitude and the b→ccs decay amplitude of the Bs meson. Combined values of the average decay width Γs and the decay width difference ΔΓs are obtained from of a multi-dimensional fit of the experimental results, extracting several other physics parameters in addition to Γs, ΔΓs and φsccs. The φsccsaverage is given further below. The correlation matrix between all physics parameters in each analysis is taken into account. Due to tensions between analyses for some of the measured parameters, scale factors are applied on their errors. The scale factors are calculated per parameter, in one dimension, using the PDG prescription. For example the scale factors of the errors of Γs, ΔΓs and φsccs are 2.45 , 1.84 and 1.00 , respectively. The scale factors are applied in a way that preserves the total correlation matrix of each analysis. The following additional constraints are then applied, using effective lifetime measurements:

  1. Bs → J/ψf0(980) lifetime measurements from CDF and D0, and Bs → J/ψπ+π− lifetime measurements from LHCb and CMS (pure CP-odd final states), which average to τ(Bs→ CP-odd) = 1.646 ± 0.013 ps, taken to be equal to (1/ΓH)×[1−(φsccs)2×ΔΓs/4];
  2. Bs → J/ψη and Bs → Ds+Ds− lifetime measurement from LHCb (pure CP-even final states), which average to τ(Bs→ CP-even) = 1.437 ± 0.014 ps, taken to be equal to (1/ΓL)×[1+(φsccs)2×ΔΓs/4];
  3. flavour-specific Bs lifetime average τ(Bs → flavour specific) = 1.527 ± 0.011 ps, taken to be equal to (1/Γs) × (1 + (ΔΓs/Γs)2/4) / (1 − (ΔΓs/Γs)2/4).
The implementation of constraints I and II, described in full in the literature [R. Fleischer and R. Knegjens, Eur. Phys. J. C (2011) 1789], neglects here possible sub-leading Penguin contributions and possible direct CP violation. The table below shows the results with and without these additional constraints. The default (i.e. recommended) set of results is the one with all the constraints applied.

Fit results from
ATLAS, CDF, CMS,
D0 and LHCb data 		without constraint
from effective
lifetime measurements 		with constraints
I and II 		with constraints
I, II and III
Γs 0.6627 ± 0.0033 ps−1 0.6575 ± 0.0025 ps−1 0.6581 ± 0.0022 ps−1
1/Γs 1.509 ± 0.008 ps    1.521 ± 0.006 ps    1.520 ± 0.005 ps   
τShort = 1/ΓL 1.425 ± 0.008 ps    1.430 ± 0.007 ps    1.429 ± 0.006 ps   
τLong = 1/ΓH 1.603 ± 0.013 ps    1.624 ± 0.009 ps    1.622 ± 0.008 ps   
ΔΓs +0.078 ± 0.006 ps−1 +0.084 ± 0.005 ps−1 +0.083 ± 0.005 ps−1
ΔΓs/Γs +0.118 ± 0.009         +0.127 ± 0.007         +0.127 ± 0.007        
correlation ρ(Γs, ΔΓs) −0.24 −0.02 +0.03

The two plots below show contours of 68% CL, in the plane (Γs, ΔΓs) on the left and in the plane (1/ΓL, 1/ΓH) on the right. The average of all Bs → J/ψφ, Bs → J/ψK+K− and Bs → ψ(2S)φ measurements (after the error scaling mentioned above) is shown as the red contour, and the constraints given by the effective lifetime measurements with CP-odd final states (Bs → J/ψf0(980) and Bs → J/ψπ+π−), 1.646 ± 0.013 ps, CP-even final states (Bs → J/ψη and Bs → Ds+Ds−), 1.437 ± 0.014 ps, and flavour-specific final states, 1.527 ± 0.011 ps, are shown as the green, pink and blue bands, respectively. The average taking all constraints into account is shown as the black filled contour. The horizontal gray band is a theory prediction ΔΓs = +0.091 ±0.015 ps−1 [J. Albrecht, F. Bernlochner, A. Lenz, and A. Rusov, arXiv:2402.04224], which assumes no new physics in Bs mixing. The vertical gray bands are calculated from the theory prediction Γd/Γs = 1.0007 ± 0.0025 [J. Albrecht, F. Bernlochner, A. Lenz, and A. Rusov, arXiv:2402.04224], assuming the experimental world average for the B0 lifetime, 1.517 ± 0.004 ps. The two solutions are due to the usage of different inputs according to [M. Bordone, B. Capdevila, and P. Gambino, PLB 822 (2021) 136679] and [F. Bernlochner et al., JHEP 10 (2022) 068].


Left plot in several formats: jpg / png / eps / pdf /         Right plot in several formats: jpg / png / eps / pdf /

(home , top , next, previous)

B0 mixing: oscillations and mass difference

Combined result on B0 mixing, obtained separately from time-dependent measurements of the oscillation frequency Δmd (at high energy colliders and asymmetric B factories) and from time-integrated measurements of the mixing probability χd at symmetric Υ(4S) machines:

Δmd = 0.5069 ± 0.0019 ps−1 from time-dependent measurements at ALEPH, DELPHI, L3, OPAL, CDF, D0, BABAR, BELLE, LHCb
χd = 0.182 ± 0.015 from time-integrated measurements at ARGUS and CLEO

Assuming no CP violation in the mixing and no width difference in the B0 system, and using the B0 lifetime average of 1.517 ± 0.004 ps (the experimental average listed above), all above measurements can be combined to yield the following world averages:

Δmd = 0.5069 ± 0.0019 ps−1
   xd = 0.7697 ± 0.0035
χd = 0.1860 ± 0.0011 		from all ALEPH, DELPHI, L3, OPAL, CDF, D0, BABAR, BELLE, LHCb, ARGUS and CLEO measurements

The plot shows the LEP and Tevatron averages, as well as all individual measurements listed as quoted by the BABAR, BELLE, BELLE II and LHCb experiments; they might assume different physics inputs. The averages (which take into account all known correlations) are quoted after adjusting the individual measurements to the common set of physics inputs. The χd average from ARGUS and CLEO is converted to a Δmd measurement assuming no CP violation, no width difference in the B0 system and a B0 lifetime of 1.517 ± 0.004 ps.


jpg / png / pdf /

The plot shows the LEP and Tevatron averages, as well as the averages quoted by the other experiments (or computed by the working group after adjusting the individual results to the common set of inputs); they might assume different physics inputs. The global averages are quoted after adjusting the all individual measurements to the common set of physics inputs. The χd average from ARGUS and CLEO is converted to a Δmd measurement assuming no CP violation, no width difference in the B0 system and a B0 lifetime of 1.517 ± 0.004 ps.


jpg / png / pdf /

(home , top , next, previous)

Bs mixing: oscillations and mass difference

Combined result on B0s mixing, obtained from time-dependent measurements of the oscillation frequency Δms at high-energy hadron colliders:

Δms = 17.765 ± 0.006 ps−1 CDF, LHCb, CMS

With a mean B0s lifetime of 1/Γs = 1.520 ± 0.005 ps, a decay width difference of ΔΓs = +0.083 ± 0.005 ps−1 and the assumption of no CP violation in B0s mixing, this leads to

xs = 26.99 ± 0.09
χs = 0.499318 ± 0.000005

The plot shows the different Δms measurement and their average.


jpg / pdf /

(home , top , next, previous)

Neutral B meson mixing: CP violation

Several different parameters can be used to describe CP violation in B mixing: |q/p|, the so-called dilepton asymmetry ASL, and the real part of εB. The relations between these parameters are as follows (all are exact except the last one which is an approximation valid for small CP violation):
   ASL = (|p/q|2−|q/p|2)/(|p/q|2+|q/p|2) = (1 − |q/p|4)/(1+|q/p|4)
   |q/p| = [(1−ASL)/(1+ASL)]**0.25
   εB = (p−q)/(p+q)
   q/p = (1−εB)/(1+εB)
   ASL ~ 4 Re(εB)/(1+|εB|2)

The parameters |q/p|, ASL and Re(εB)/(1+|εB|2) are thus equivalent. There is CP violation in the mixing if |q/p| is different from 1, i.e. ASL is different from 0.

Averages are given below separately for the B0 and the Bs systems. Two sets of averages are given for the B0 system in the first table: a first set using only measurements performed at Υ(4S) machines, and a second set using all measurements (excluding those that assume no CP violation in Bs mixing). The second table presents an average for the Bs system. Measurements performed at high energy that do not separate the B0 and Bs contributions are no longer used to obtain the final averages (at this time, the only measurements at high energy used in the averages are from D0 and LHCb).

CP-violating observable in B0 mixing
|q/p| = 1.0009 ± 0.0013
ASL = −0.0019 ± 0.0027
Re(εB)/(1+|εB|2) = −0.0005 ± 0.0007
from measurements at the Υ(4S)
|q/p| = 1.0010 ± 0.0008
ASL = −0.0021 ± 0.0017
Re(εB)/(1+|εB|2) = −0.0005 ± 0.0004
world average

CP-violating observable in Bs mixing
|q/p| = 1.0003 ± 0.0014
ASL = −0.0006 ± 0.0028
world average

The above world averages ASL(B0) = −0.0021 ± 0.0017 and ASL(Bs) = −0.0006 ± 0.0028 are obtained from a two-dimensional fit of the CLEO, BABAR, Belle, D0 and LHCb results: the correlation coefficient between them is found to be −0.054 . This is illustrated in the plot below, where the black ellipse represents the world average. The orange vertical band shows the B-factory average of ASL(B0) (measurements performed by CLEO, BABAR and Belle at the Υ(4S)), the two brown ellipses the D0 measurements, and the green ellipse the LHCb measurements; the grey ellipse is an average including only untagged B0(s) → D(*)(s) μ X decays measured by D0 and LHCb. The white point close to (0,0) is the Standard Model prediction [J. Albrecht, F. Bernlochner, A. Lenz, and A. Rusov, arXiv:2402.04224]. The prediction and world average are consistent with each other at the level of 0.5 σ.


jpg / png / pdf /

CP violation in Bs mixing is caused by the weak phase difference φ12=arg[−M12/Γ12], where M12 and Γ12 are the off-diagonal elements of the mass and decay matrices. The tangent of this phase difference can be estimated (approximately) as ASL(Bs) Δms/ΔΓs= −0.1 ± 0.6 using the above averages of ASL(Bs), Δms and ΔΓs.

(home , top , next, previous)

CP-violating phase in the interference between Bs-mixing and decay in b→ccs transitions

The weak phase φsccs describing CP violation in the interference between Bs mixing and decay in b→ccs transitions (for example Bs → J/ψφ) is predicted by the Standard Model to be approximately equal to −2βs, where βs = arg(−(Vts Vtb*)/(Vcs Vcb*)) ~ 1 degree. The phase −2βs is the equivalent of 2β for the B0 meson. The phase φsccs has been measured in several analyses: Bs → J/ψφ analyses from CDF, D0, ATLAS and CMS, and analyses from LHCb of the decay modes Bs → J/ψK+K− (including Bs → J/ψφ), Bs → ψ(2S)φ, Bs → J/ψπ+π− and Bs → Ds+Ds−. A combined multi-dimensional fit of φsccs, ΔΓs, Γs and other physics parameters is performed. The correlation matrix between all physics parameters in each analysis is taken into account. Due to tensions between analyses for some of the measured parameters, scale factors are applied on their errors. The scale factors are calculated per parameter, in one dimension, using the PDG prescription. For example the scale factors of the errors of Γs, ΔΓs and φsccs are 2.51 , 1.88 and 1.00 , respectively. The scale factors are applied in a way that preserves the total correlation matrix of each analysis. The combination is then repeated keeping only the Bs → J/ψK+K− analyses, to get an average for φsJ/ψKK; in this case the scale factors of the errors of Γs, ΔΓs and φsJ/ψKK are 2.47 , 1.86 and 1.00 , respectively.

Combined result from
CDF, D0, ATLAS, CMS and LHCb data
(complete list of inputs and references)
φsccs −0.040 ± 0.016
φsJ/ψφ −0.050 ± 0.017

The plots below show some of the results of the multi-dimensional fits, including all on the left and only the Bs → J/ψφ analyses on the right. The plots on the top show, in the (φsccs, ΔΓs) plane, the individual 68% confidence-level contours of ATLAS, CMS, CDF, D0 and LHCb, their combined contour (black solid line and shaded area), as well as the Standard Model predictions (very thin white rectangle). The prediction for φsccs is taken as the indirect determination of −2βs via a global fit to experimental data within the Standard Model, −2βs = −0.0376 +0.0006 −0.0005 [J. Charles et al. (CKMfitter), Phys. Rev. D91, 073007 (2015), updated with Summer 2023 results] and −0.0367 ± 0.0010 [M. Bona et al. (UTfit), Rend. Lincei Sci. Fis. Nat. 34, 27 (2023), updated with Summer 2023 results], while the Standard Model prediction for ΔΓs is +0.091 ±0.015 ps−1 [J. Albrecht, F. Bernlochner, A. Lenz, and A. Rusov, arXiv:2402.04224]. The combined result is consistent with these predictions. The plots on the bottom show, in the (Γs, ΔΓs) plane, the individual 68% confidence-level contours of ATLAS, CMS, CDF, D0 and LHCb, their combined contour (black solid line and shaded area), as well as the Standard Model prediction for ΔΓs (horizontal gray band). Because of tensions between the measurements, the errors on Γs and ΔΓs have been scaled by the indicated factors (the ellipses representing the results of each experiment are shown before scaling, while the combined ellipses include the scale factors).



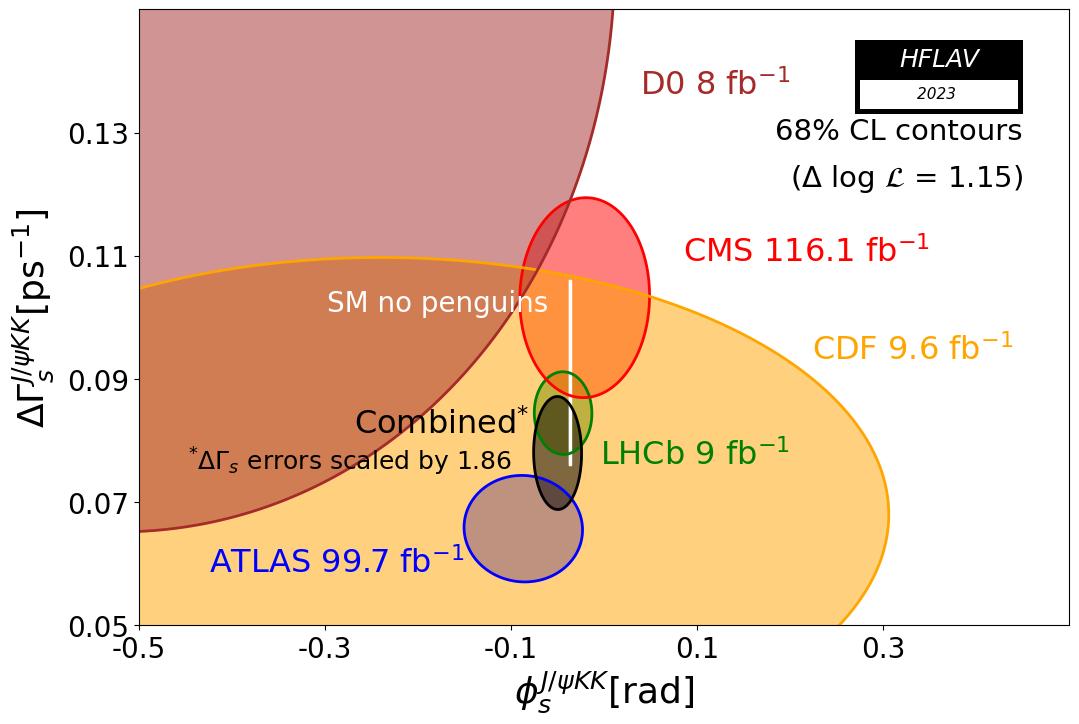
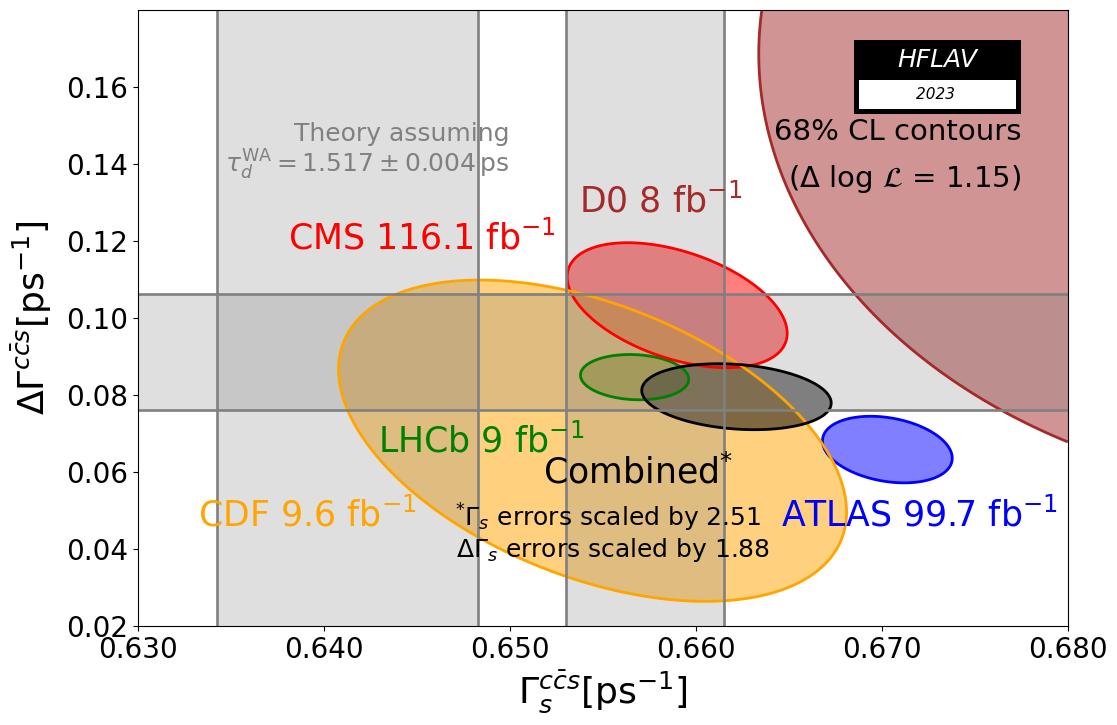
Top left plot in several formats: jpg / png / pdf / eps /         Top right plot in several formats: jpg / png / pdf / eps /
Bottom left plot in several formats: jpg / png / pdf / eps /         Bottom right plot in several formats: jpg / png / pdf / eps /

A complete list of inputs and references from CDF, D0, ATLAS, CMS and LHCb, as well as the results for φsccs and ΔΓs from the mutli-dimensional fit of all b→ccs results, is available here.

(home , top , next, previous)

b-hadron fractions

We no longer update our averages for the b-hadron fractions in unbiased samples of weakly-decaying b-hadrons produced in in Υ(4S) decays, in Υ(5S) decays, in Z decays, in pp collisions at 1.8−2 TeV, and in high-energy pp collisions. Similarly we no longer provide the time-integrated mixing probability χ, averaged over the b-hadrons species, in the high-energy environments.

Please refer to our latest updates performed in 2020.

The b-hadron fractions in Υ(4S) decays and in Υ(5S) decays are maintained by the "B to charm" HFLAV sub-group.

The b-hadron fractions in Z decays have been stable over many years, without new measurements becoming available.

The fractions of b-hadron produced at high-energy colliders were computed under the assumption that they are the same in Z decays at LEP, in pp collisions at the Tevatron (√s=1.8−2 TeV) or in proton-proton collisions at the LHC (√s=7−13 TeV). While this assumption was plausible in the past, it is now known since several years that it is incorrect. The available data show that the fractions depend on the kinematics of the produced b hadron. Both CDF and LHCb reported a transverse-momentum (pT ) dependence of the fractions, with the fraction of Λb baryons observed at low pT being enhanced with respect to that seen at LEP at higher pT. Other dependences (e.g. on pseudo-rapidity) are also expected.


Author: OS 03-apr-2024
Latest mod. Thu Mar 28 04:52:43 PM CET 2024