Global Fit for D0-
D0 Mixing
(allowing for CP violation)
(updated 31 March 2019)
People working on this:
Alan Schwartz,
Marco Gersabeck
For a complete list of references click
here
For world average values of measured observables (used below) click
here
Notation:
The mass eigenstates are denoted
D 1 ≡ p|D0> +
q|D0> and
D 2 ≡ p|D0> −
q|D0>;
δ and δKππ are strong phase differences
between
D0
→ f and D0 → f amplitudes, and
φ is the weak phase difference Arg(q/p). We define
δ ≡
δ D0 → K−n(π)
−
δ D0
→ K−n(π).
The mixing parameters are defined as
x ≡ (m2 − m1)/Γ and
y ≡ (Γ2 − Γ1)/(2Γ), where
Γ = (Γ1 + Γ2)/2.
Our convention is (CP)|D0> =
−|D0>
and
(CP)|D0> =
−|D0>; thus, in the absence of CP violation,
x = (mCP+ − mCP−)/Γ and
y = (ΓCP+ − ΓCP−)/(2Γ).
Experimental Observables:
From all experiments there are 49 observables:
y CP ,
A Γ ,
(x, y, |q/p|, φ) Belle
K0S π+ π − ,
(x, y) LHCb
K0S π+ π − ,
(x, y) BaBar
K0S h+ h− ,
(x, y) BaBar
π0 π+ π− ,
(R M )/2 LHCb
K+ π− π+ π − ,
(R M ) semileptonic ,
(x", y")
K+ π− π 0 ,
(R D , x2, y, cos δ, sin δ)
Ψ(3770) ,
(RD, AD, x'2±,
y'±)BaBar ,
(RD, AD, x'2±,
y'±)Belle ,
(RD, x'2, y')CDF ,
(RD±, x'2±, y'±)LHCb ,
(ACPK,
ACPπ)BaBar ,
(ACPK,
ACPπ)Belle ,
(ACPK −
ACPπ)CDF ,
(ACPK −ACPπ)
LHCb(D*) ,
(ACPK −ACPπ)
LHCb(B →D0μX)
Theoretical Parameters:
Allowing for CP violation, there are 10 underlying parameters:
x, y, δ, δKππ,
RD,
AD, Aπ, AK,
|q/p|, and Arg(q/p) = φ.
The first two parameters govern mixing; the next two are
strong phases; R D is the ratio
Γ(D0→
f)/Γ(D0 → f);
the next three are direct CP-violating asymmetries for
D0 → K+ π−,
D0 → π+ π−, and
D0 → K+ K−, respectively;
and the last two are indirect CP-violating parameters.
The relationships between these parameters and the measured
observables are given below. The observables appear in
blue
(on the left sides of the equations), the underlying parameters in
magenta
(on the right sides), and intermediate variables in black.

Measurements used:
| Index |
Observable |
Value |
Source |
| 1 |
y CP |
(0.715 ± 0.111)% |
World average (COMBOS combination)
of D0 → K+ K− /
π+ π − /
K+ K− K0
|
| 2 |
A Γ |
(−0.032 ± 0.026)% |
World average (COMBOS combination)
of D0 → K+ K− /
π+ π − results
|
| |
| x (no CPV) |
| y (no CPV) |
| |
| |
| |q/p| (no dCPV) |
| Arg(q/p)=φ (no dCPV) |
| |
| |
| x |
| y |
| |q/p| |
| φ |
|
| |
| 0.56 ± 0.19 +0.067 −0.127
|
| 0.30 ± 0.15 +0.050 −0.078
|
| |
| 0.90 +0.16 −0.15
+0.078 −0.064
|
| (−6 ± 11 +4.2 −5 )
degrees |
| |
| (0.58 ± 0.19 +0.0734 −0.1177 )%
|
| (0.27 ± 0.16 +0.0546 −0.0854 )%
|
| 0.82 +0.20 −0.18
+0.0807 −0.0645
|
| (−13 +12 −13
+4.15 −4.77 ) degrees |
|
Belle D0 → K0 S
π+ π − results using
921 fb−1.
|
Correlation coefficient is +0.012 for no-CPV; for CPV-allowed they are:
|
| 1 | | 0.054 | |
−0.074 | | −0.031 |
| 0.054 | | 1 | |
0.034 | | −0.019 |
| −0.074 | | 0.034 |
|
1 | | 0.044 |
| −0.031 | | −0.019 | |
0.044 | | 1 |
|
| |
| x (no CPV) |
| y (no CPV) |
| |
| xCP |
| yCP |
| Δx |
| Δy |
|
| (−0.86 ± 0.53 ± 0.17)% |
| (0.03 ± 0.46 ± 0.13)% |
| |
| (0.27 ± 0.16 ± 0.04)% |
| (0.74 ± 0.36 ± 0.11)% |
| (−0.053 ± 0.070 ± 0.022)% |
| (0.06 ± 0.16 ± 0.03)% |
|
|
LHCb
D0 →
K0S π+π −
results using 1 fb-1 (√s = 7 TeV) |
|
Correlation coefficient = +0.37, no CPV. |
| |
|
3 fb-1 results (√s = 7, 8 TeV) allowing for CPV. |
|
Correlation coefficients (statistical + systematic): |
| 1 | | (−0.17 + 0.15) |
| (0.04 + 0.01) | |
(−0.02 − 0.02) |
| | | 1 |
| (−0.03 − 0.05) |
| (0.01 − 0.03) |
| | | | |
1 | | (−0.13 + 0.14) |
|
| For (x, y, |q/p|, φ) → (xCP, yCP, Δx, Δy)
mapping, see
PRD 99, 012007 (2019)
|
|
| 11-12 |
|
| (0.16 ± 0.23 ± 0.12 ± 0.08)% |
| (0.57 ± 0.20 ± 0.13 ± 0.07)% |
|
|
BaBar
D0 →
K0S π+π − and
D0 →
K0S K+ K − combined; |
|
Correlation coefficient = +0.0615, no CPV. |
|
| 13-14 |
|
| (1.5 ± 1.2 ± 0.6)% |
| (0.2 ± 0.9 ± 0.5)% |
|
|
BaBar
D0 →
π0 π+π − |
|
Correlation coefficient = −0.006, no CPV. |
|
| 15 |
(x2 + y2)/2 |
(0.0130 ± 0.0269)% |
World average (COMBOS combination)
of
D0 → K+l− ν results |
| 16-17 |
|
| (2.61 +0.57 −0.68 ± 0.39)% |
| (−0.06 +0.55 −0.64 ± 0.34)% |
|
|
BaBar
K+ π − π 0 result;
correlation coefficient = −0.75. |
|
Note: x" = x cos δKππ + y sin δKππ,
y" = y cos δKππ − x sin δKππ. |
|
| 18 |
|
| (0.533 ± 0.107 ± 0.045)% |
| (0.06 ± 0.23 ± 0.11)% |
| (4.2 ± 2.0 ± 1.0)% |
| 0.81 +0.22−0.18
+0.07−0.05 |
| −0.01 ± 0.41 ± 0.04 |
|
CLEO-c Ψ(3770) results; correlation coefficients:
| 1 | |
0 | |
0 | |
−0.42 | |
0.01 |
| | | 1 | |
−0.73 | | 0.39 | |
0.02 | |
| | | | |
1 | | −0.53 |
| −0.03 |
| | | | |
| | 1 |
| 0.04 |
| | | | |
| | |
| 1 |
|
| 19 |
|
| (0.303 ± 0.0189)% |
| (−0.024 ± 0.052)% |
| (0.98 ± 0.78)% |
|
BaBar
K+ π − results; correlation coefficients:
| 1 | | +0.77 | | −0.87 |
| +0.77 | | 1 | | −0.94 |
| −0.87 | | −0.94 | | 1 |
|
| 20 |
|
| (−2.1 ± 5.4)% |
| (−0.020 ± 0.050)% |
| (0.96 ± 0.75)% |
|
BaBar
K+ π − results; correlation coefficients
same as above.
|
| 21a |
|
| (0.353 ± 0.013)% |
| (0.009 ± 0.022)% |
| (0.46 ± 0.34)% |
|
Belle
K+ π − no-CPV results using 976 fb−1.
Correlation coefficients:
| 1 | | +0.737 | | −0.865 |
| +0.737 | | 1 | | −0.948 |
| −0.865 | | −0.948 | | 1 |
|
| 21b |
|
| (0.364 ± 0.018)% |
| (0.032 ± 0.037)% |
| (−0.12 ± 0.58)% |
|
Belle
K+ π − CPV-allowed results using
400 fb−1. Correlation coefficients:
| 1 | | +0.655 | | −0.834 |
| +0.655 | | 1 | | −0.909 |
| −0.834 | | −0.909 | | 1 |
|
| 22 |
|
| (2.3 ± 4.7)% |
| (0.006 ± 0.034)% |
| (0.20 ± 0.54)% |
|
|
Belle
K+ π − CPV-allowed results using
400 fb−1;
|
|
correlation coefficients same as above.
|
|
| 23 |
|
| (0.351 ± 0.035)% |
| (0.008 ± 0.018)% |
| (0.43 ± 0.43)% |
|
CDF
K+ π − results for 9.6 fb−1.
Correlation coefficients:
| 1 | | 0.90 | | −0.97 |
| 0.90 | | 1 | | −0.98 |
| −0.97 | | −0.98 | | 1 |
|
| 24 |
|
| (0.3454 ± 0.0045)% |
| (0.0061 ± 0.0037)% |
| (0.501 ± 0.074)% |
|
LHCb K+ π − results for
5.0 fb−1 (√s = 7, 8 TeV)
Correlation coefficients:
| 1 | | 0.843 | | −0.935 |
| 0.843 | | 1 | | −0.963 |
| −0.935 | | −0.963 | | 1 |
|
| 25 |
|
| (0.3454 ± 0.0045)% |
| (0.0016 ± 0.0039)% |
| (0.554 ± 0.074)% |
|
LHCb K+ π − results for
5.0 fb−1 (√s = 7, 8 TeV)
Correlation coefficients:
| 1 | | 0.846 | | −0.935 |
| 0.846 | | 1 | | −0.964 |
| −0.935 | | −0.964 | | 1 |
|
| 26 |
|
| (0.00 ± 0.34 ± 0.13)% |
| (−0.24 ± 0.52 ± 0.22)% |
|
BaBar 385.8 fb−1 near ϒ(4S) resonance
|
| 27 |
|
| (−0.32 ± 0.21)% |
| (0.31 ± 0.22)% |
|
|
CDF 9.7 fb−1
pp collisions at
√s = 1.96 TeV |
|
( 〈t〉K − 〈t〉π )
/ τD = 0.27 ± 0.01 |
|
| 28 |
ACPK − ACPπ |
(−0.154 ± 0.029)% |
|
LHCb 9.0 fb−1 pp collisions at
√s = 7, 8, 13 TeV |
| D*+ → D0π+
and
B → D0μ− X flavor tags |
|
( 〈t〉K − 〈t〉π )/τD
= 0.115 ± 0.002;
〈t〉/τD
= 1.71 ± 0.10
|
|
| 29 |
(x2 + y2)/4 |
(0.0048 ± 0.0018)% |
|
LHCb 3.0 fb−1 pp collisions at
√s = 7, 8 TeV |
|
D0 →
K+ π − π + π −
|
|
MINUIT fit results:
note that x, y, R D, A D,
A π and A K are in
percent; δ, δ2 (=δKππ),
and φ are in radians.
Fit #1:
no CP violation
(AD= 0,
AK= 0,
Aπ= 0,
|q/p| = 1, φ = 0)

Fit #2a:
no direct CP violation in doubly-Cabibbo-suppressed amplitudes
(AD= 0)
In addition, we impose the relation
tanφ = (1-|q/p|2)/(1+|q/p|2) × (x/y)
to reduce four independent parameters to three. This relation was first
derived by
Ciuchini et al.
and was later independently obtained by
Kagan and Sokoloff.
Alternatively, one can use the quadratic equation (15) of
Grossman, Nir, and Perez
to reduce four parameters to three
(e.g., see here).
We use the Ciuchini/Kagan formula to perform two separate fits: first we
float x, y, and φ and from them derive |q/p| (this yields proper errors
for φ). Then we float x, y, and |q/p| and from them derive φ (this
yields proper errors for |q/p|).
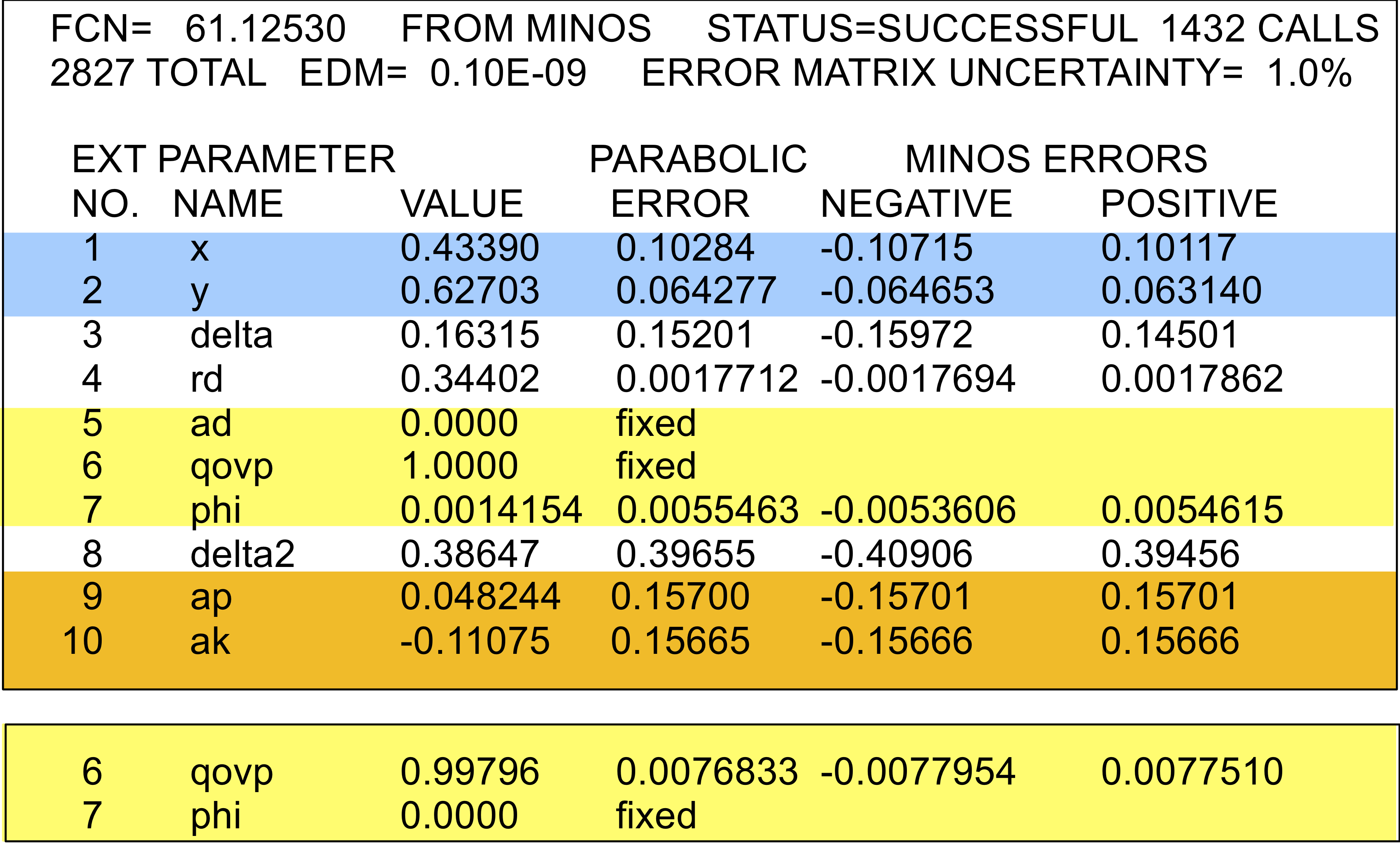
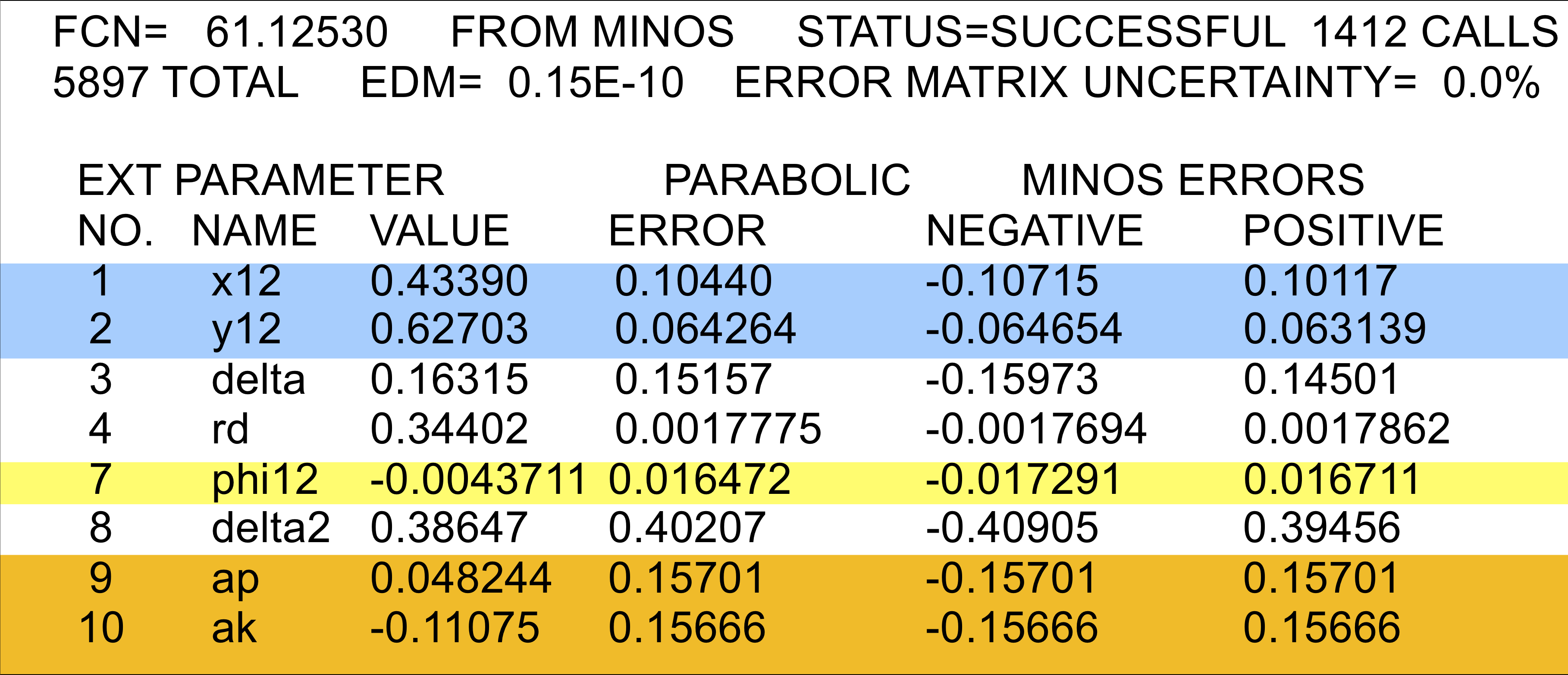
Fit #2b:
no direct CP violation in doubly-Cabibbo-suppressed amplitudes
(AD= 0)
fit for theory parameters x12, y12, and φ12
Here we fit for the underlying theory parameters
x12 ≡ 2|M12|/Γ,
y12 ≡ |Γ12|/Γ,
and φ12 ≡ Arg(M12/Γ12).
The relationships between these parameters and our nominal
parameters (x, y, |q/p|, φ) are given by
Kagan and Sokoloff Eqs. (14, 15, 48, 52), but a
factor of 2-1/2 is missing from Eqs. (14) and (15).
An alternative derivation (our own) is
here;
these differ from Kagan and Sokoloff but give identical results.
Fit #3:
allowing all CP violation
(all parameters floated)
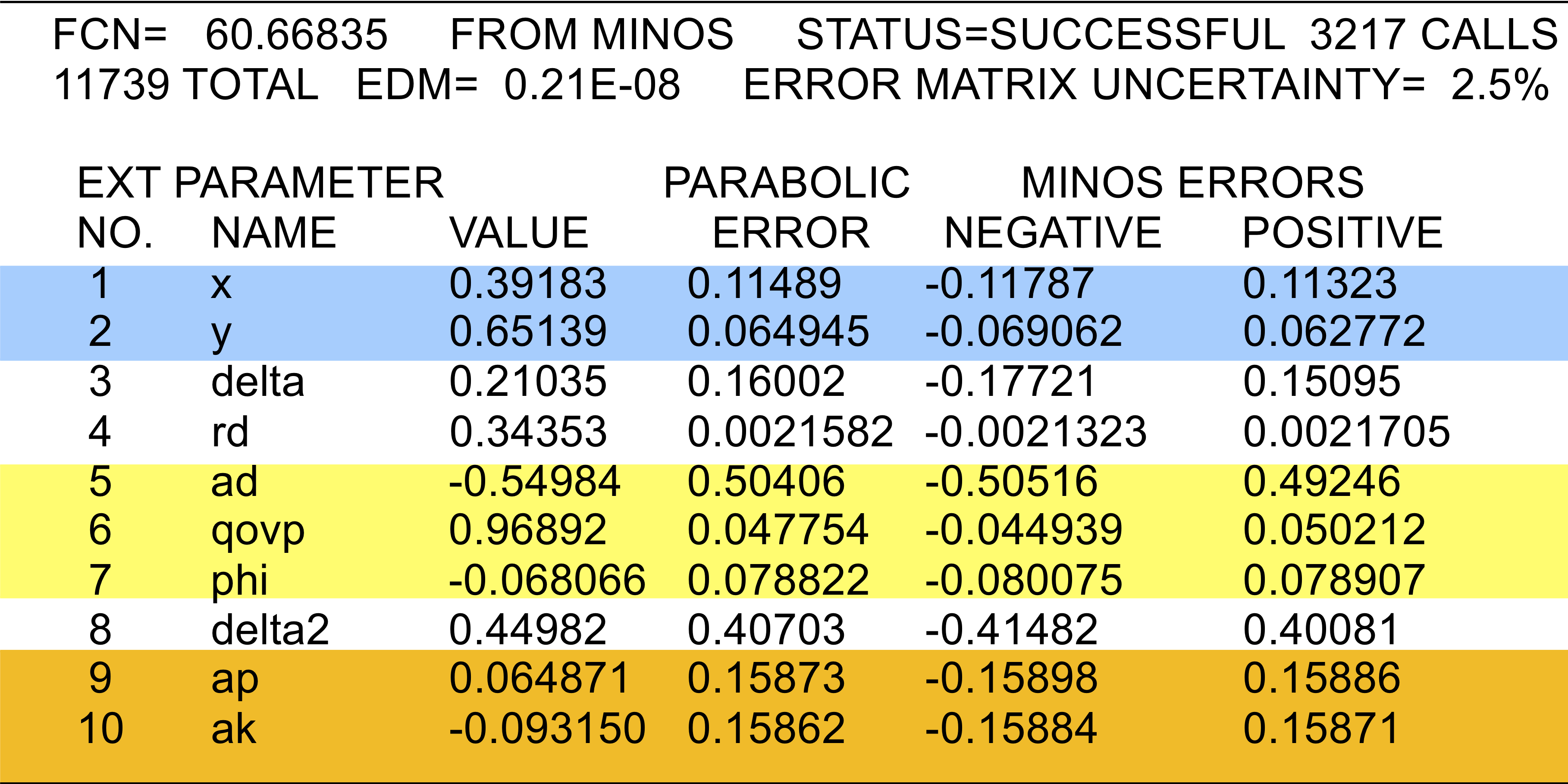
The final results are:

Note that for the No-direct-CPV results, the values listed for
(δ, δKππ, RD) are from Fit 2a
rather than Fit 2b (but they are almost identical).
MIGRAD correlation coefficients:

χ 2 contributions:
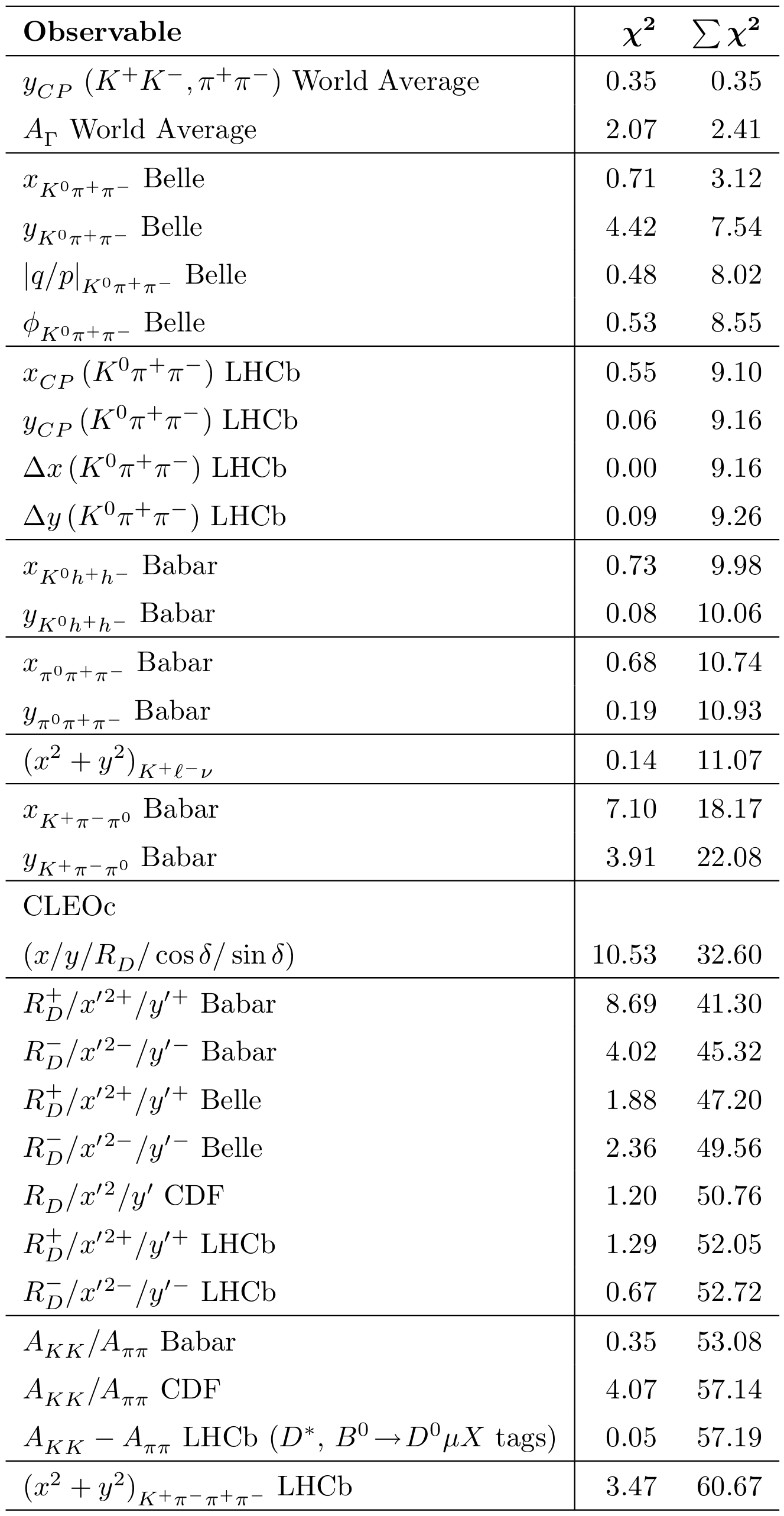 _____________________________________________
_____________________________________________
MNCONTOUR-like 2-d plots (click on for high resolution):
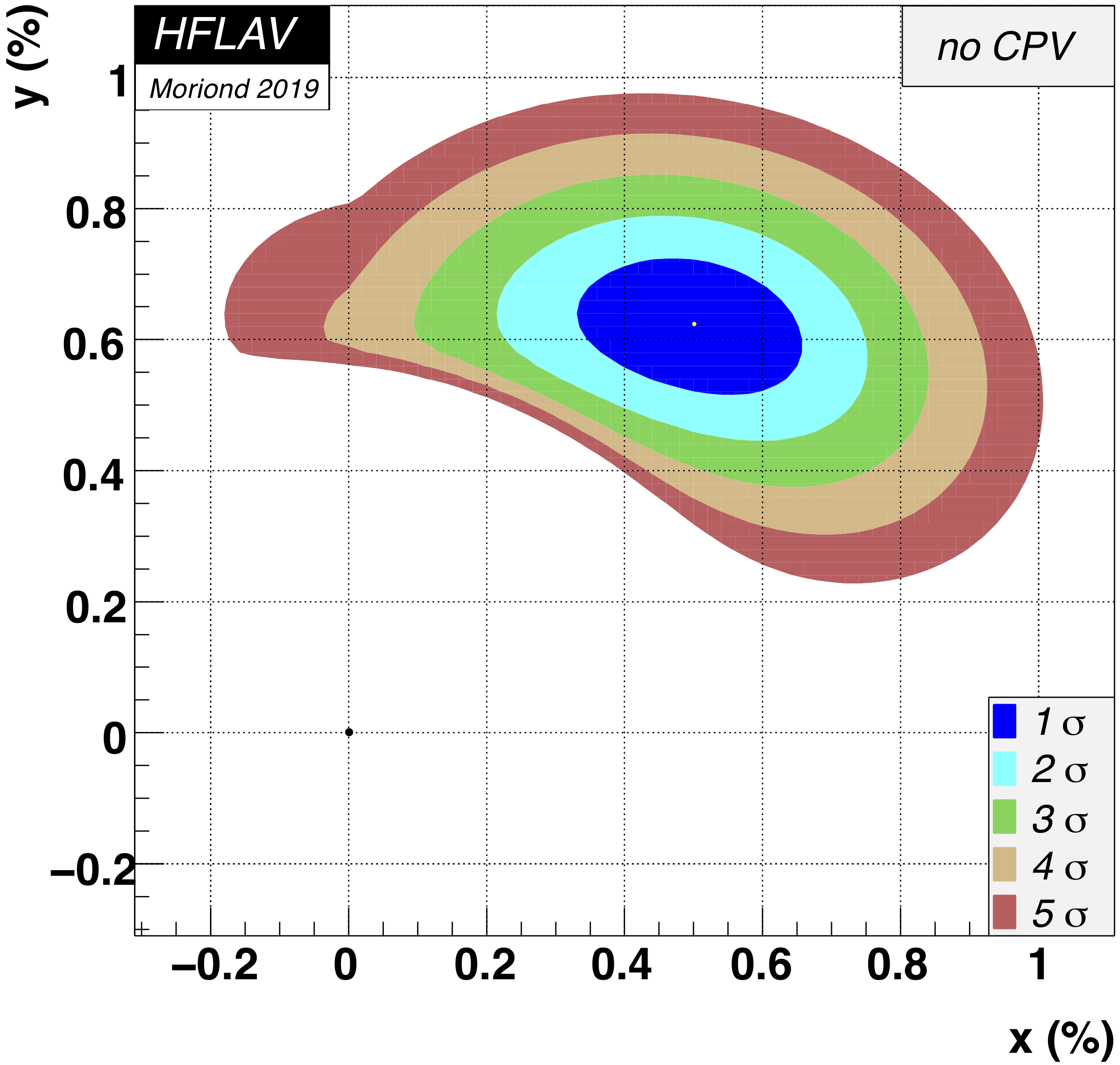

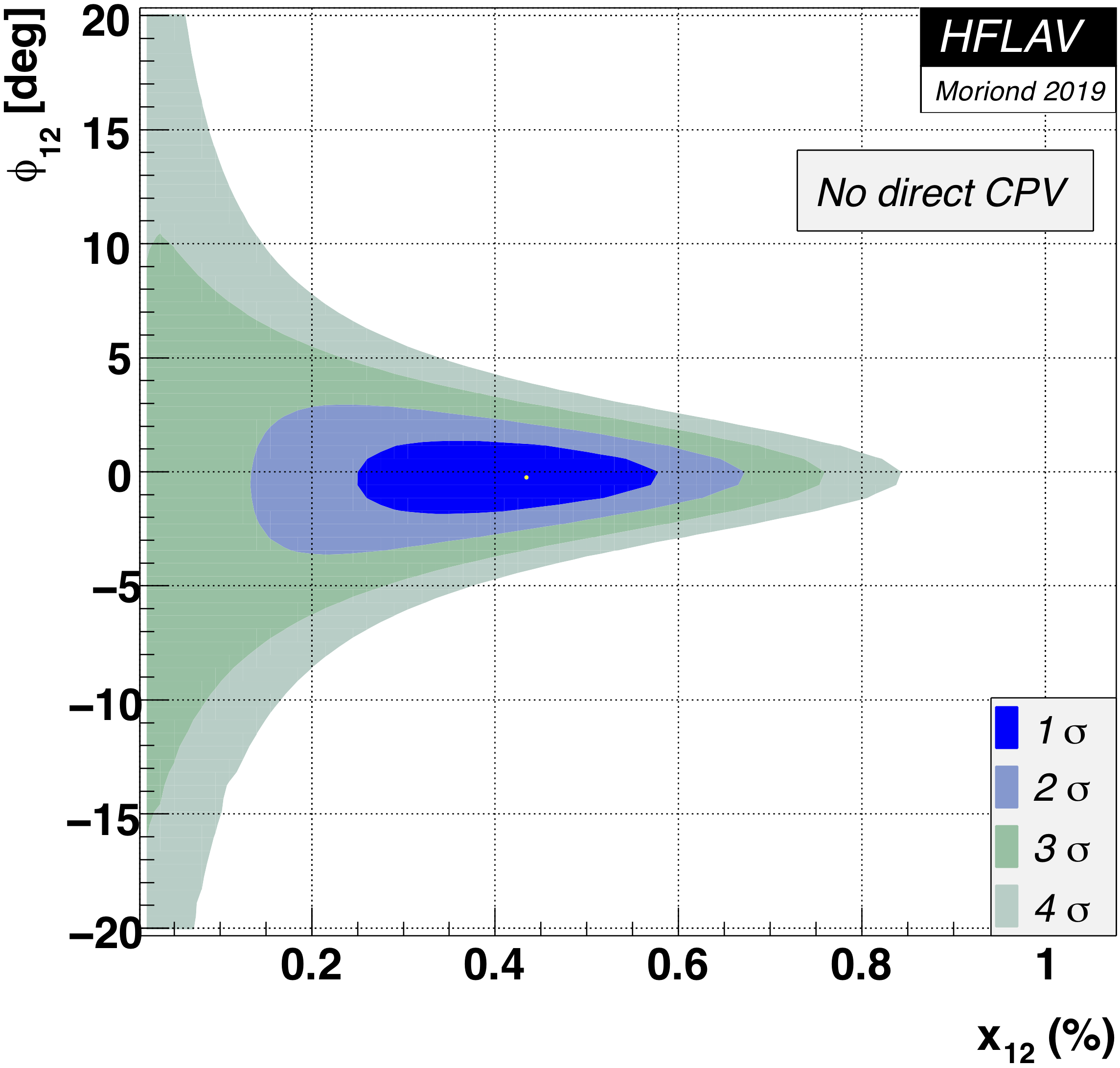
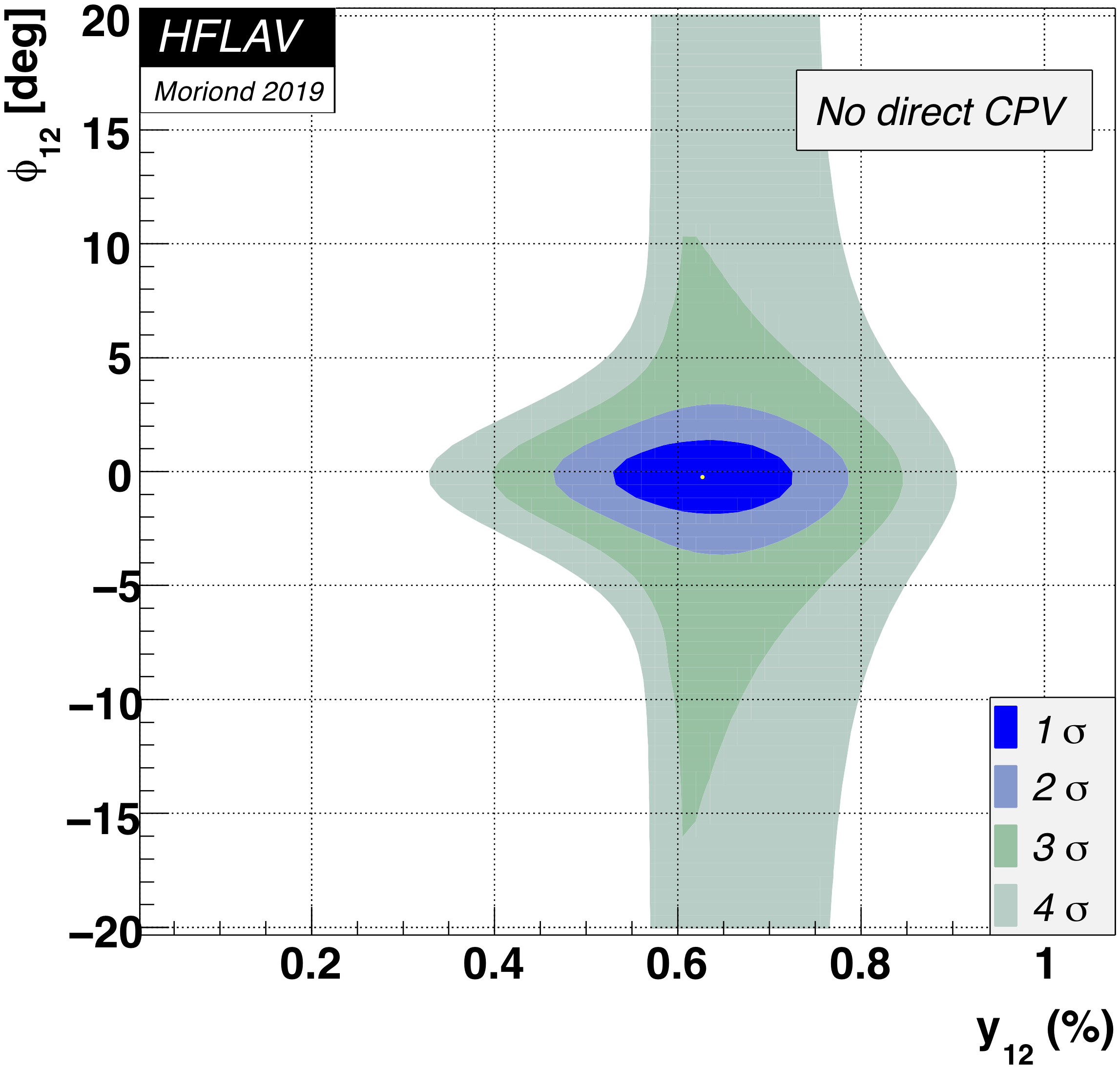
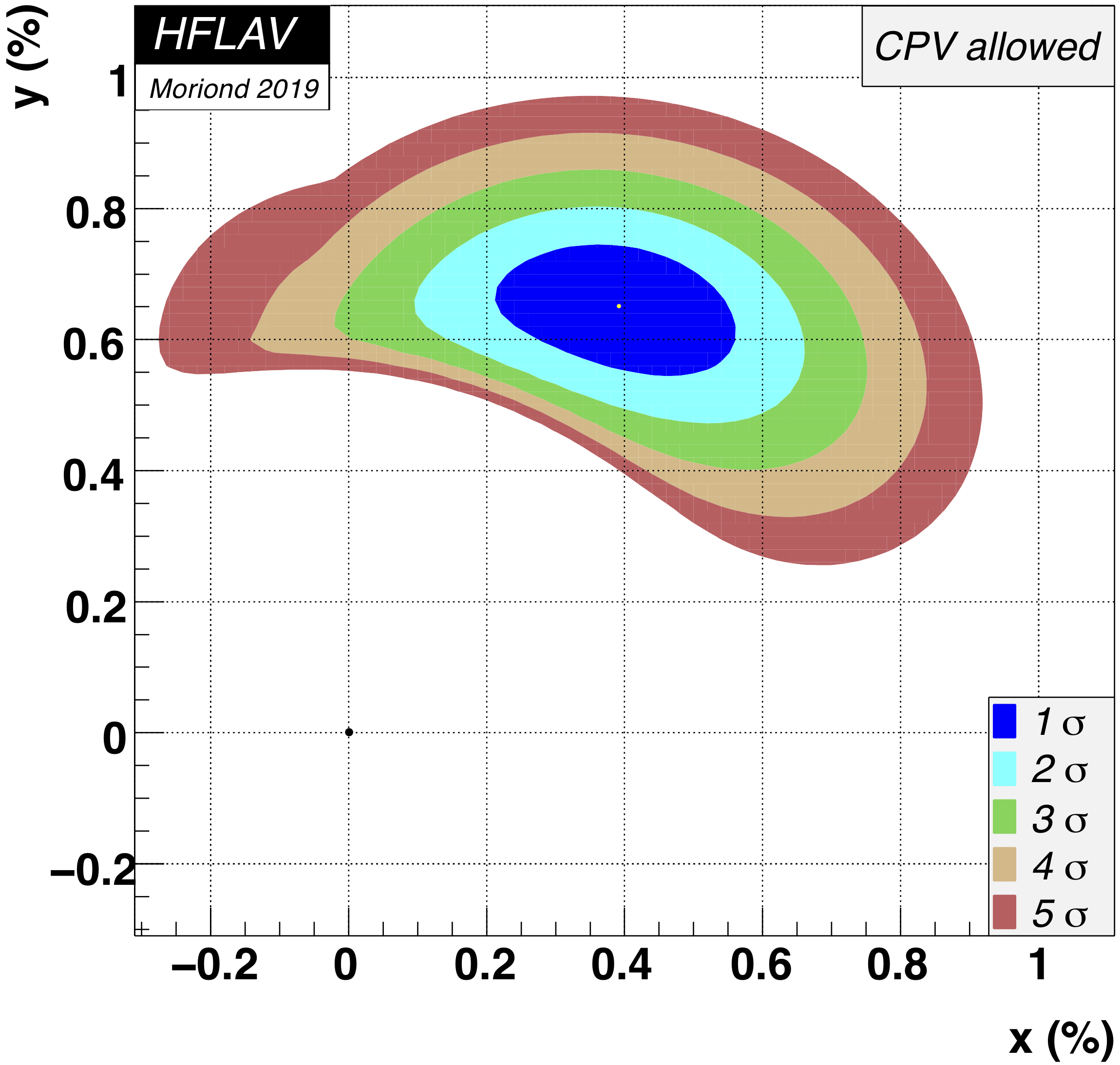
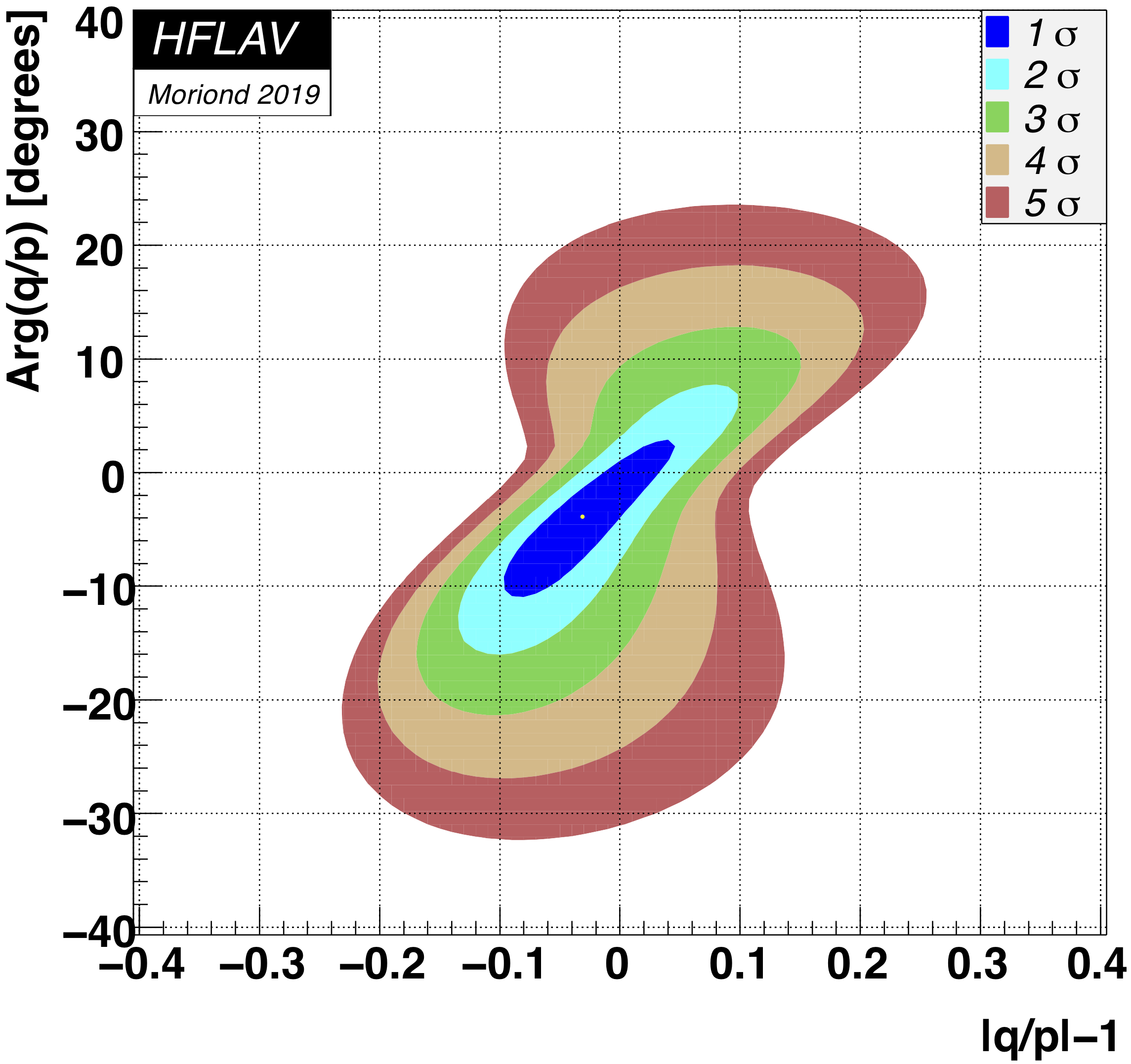
Old scales (for comparison):
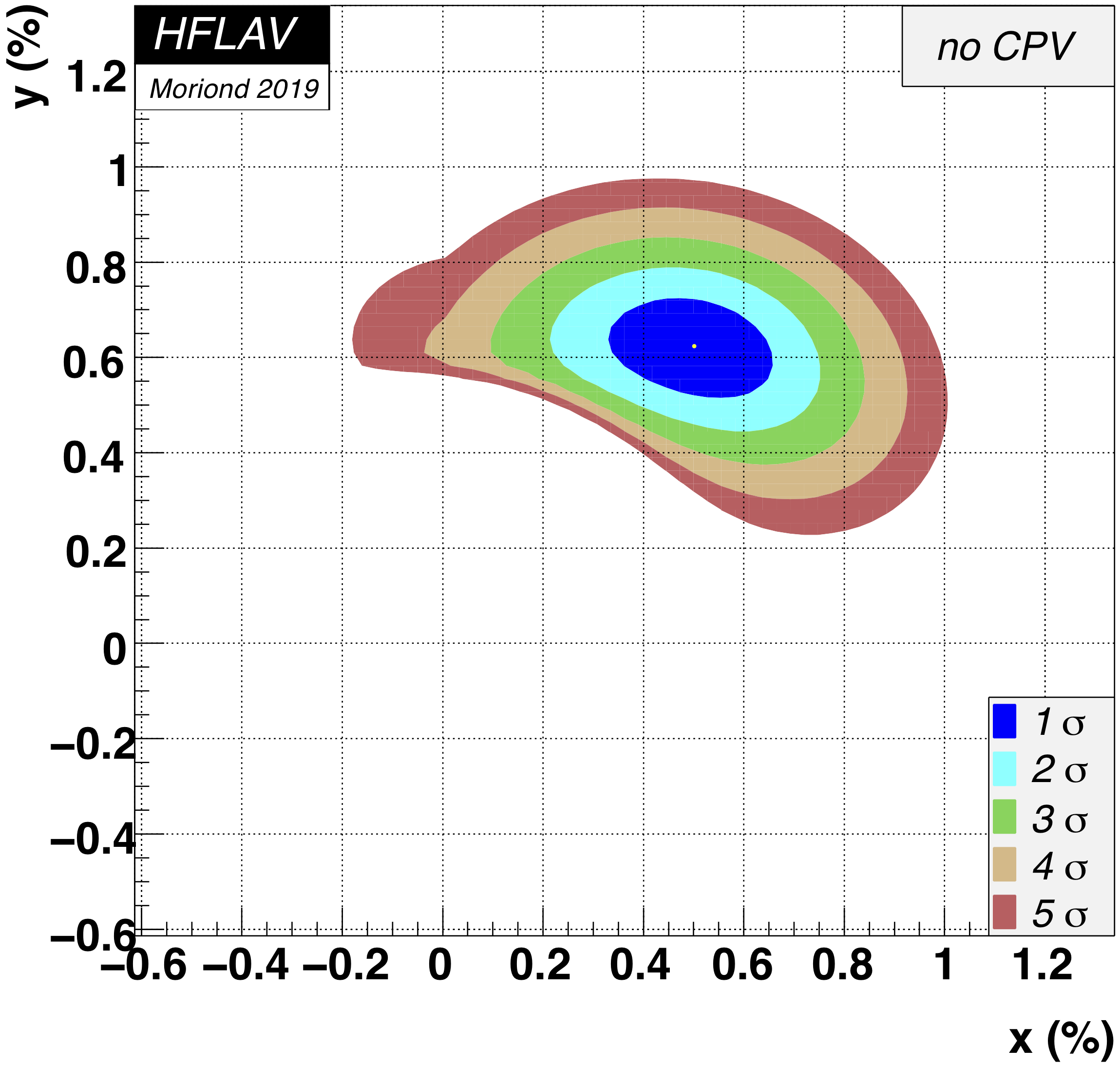
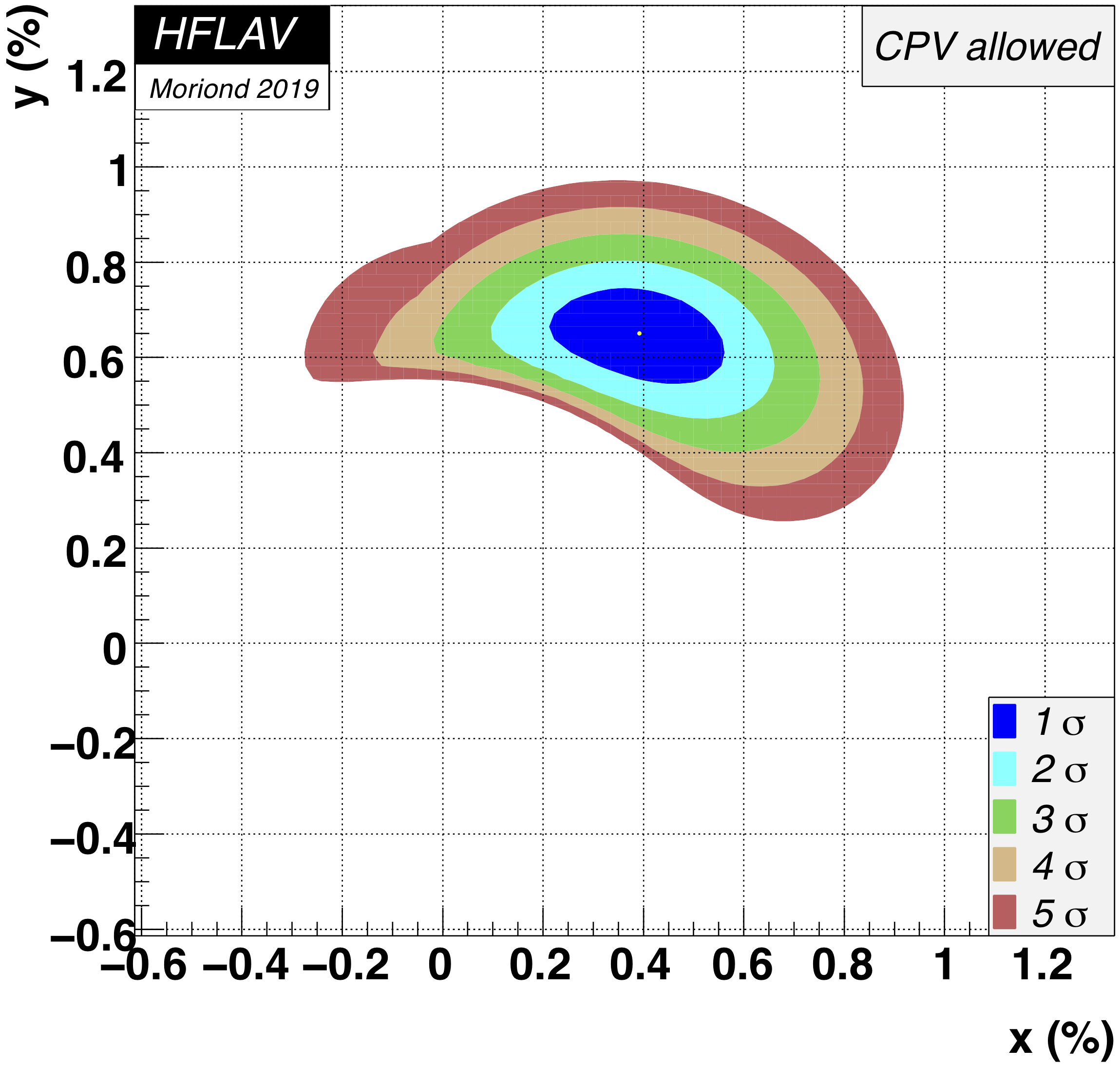
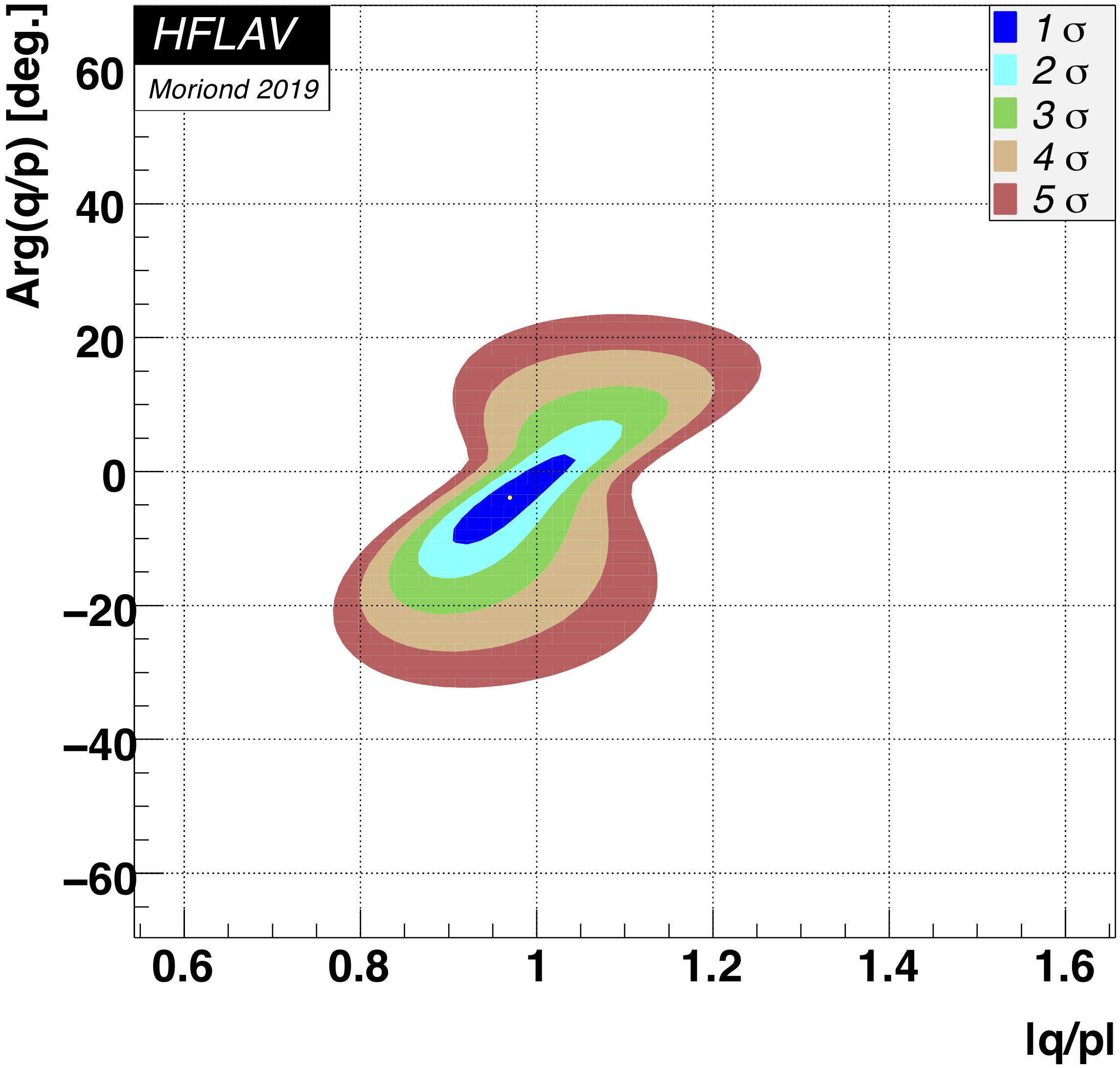
CPV-allowed plot, no mixing (x,y) = (0,0) point:
Δ χ 2 = 2028,
excluded at ≫ 11.5σ (limit of PROB routine)
No CPV (|q/p|, φ) = (1,0) point:
Δ χ 2 = 0.935,
CL = 0.63
_____________________________________________
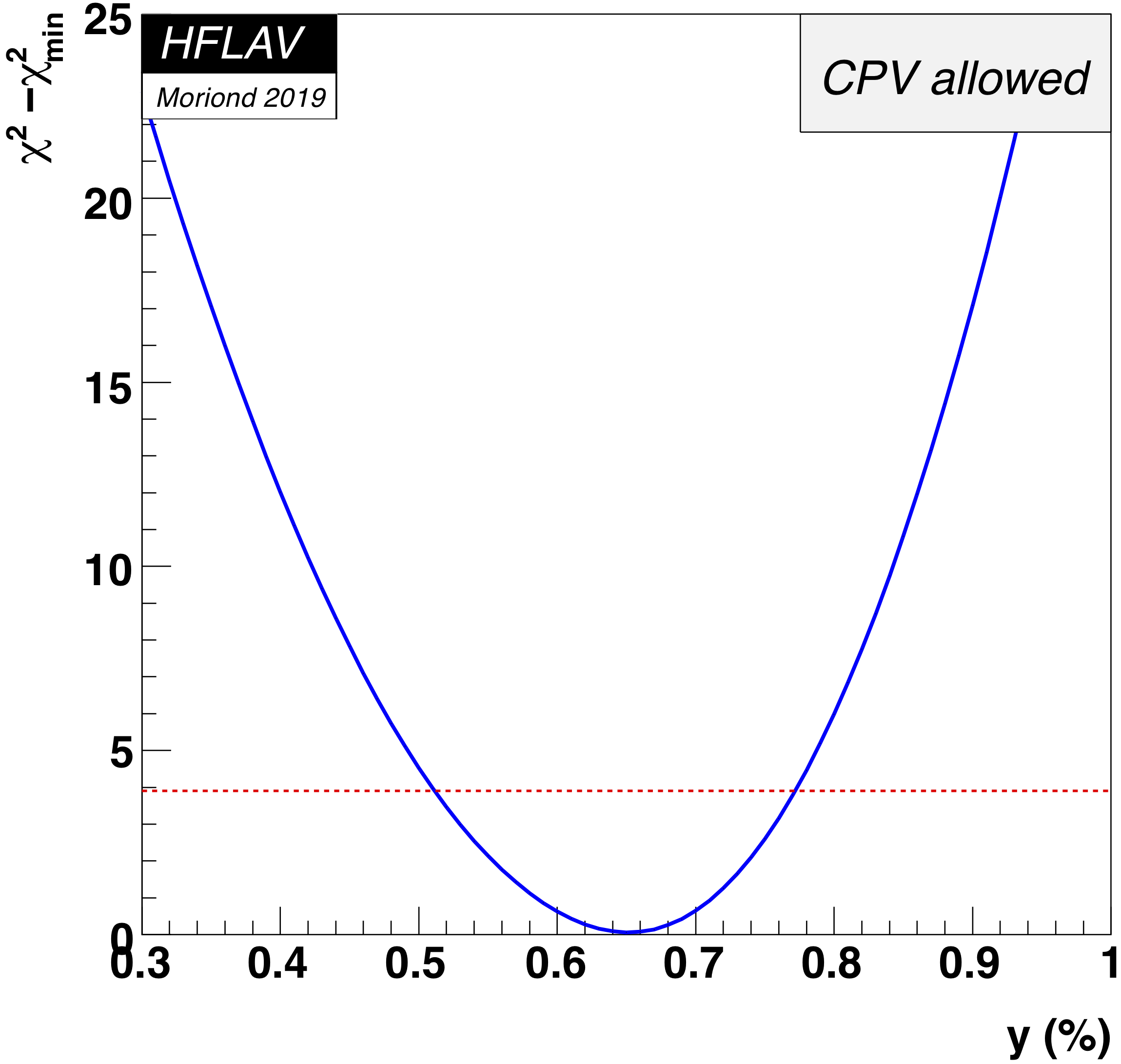
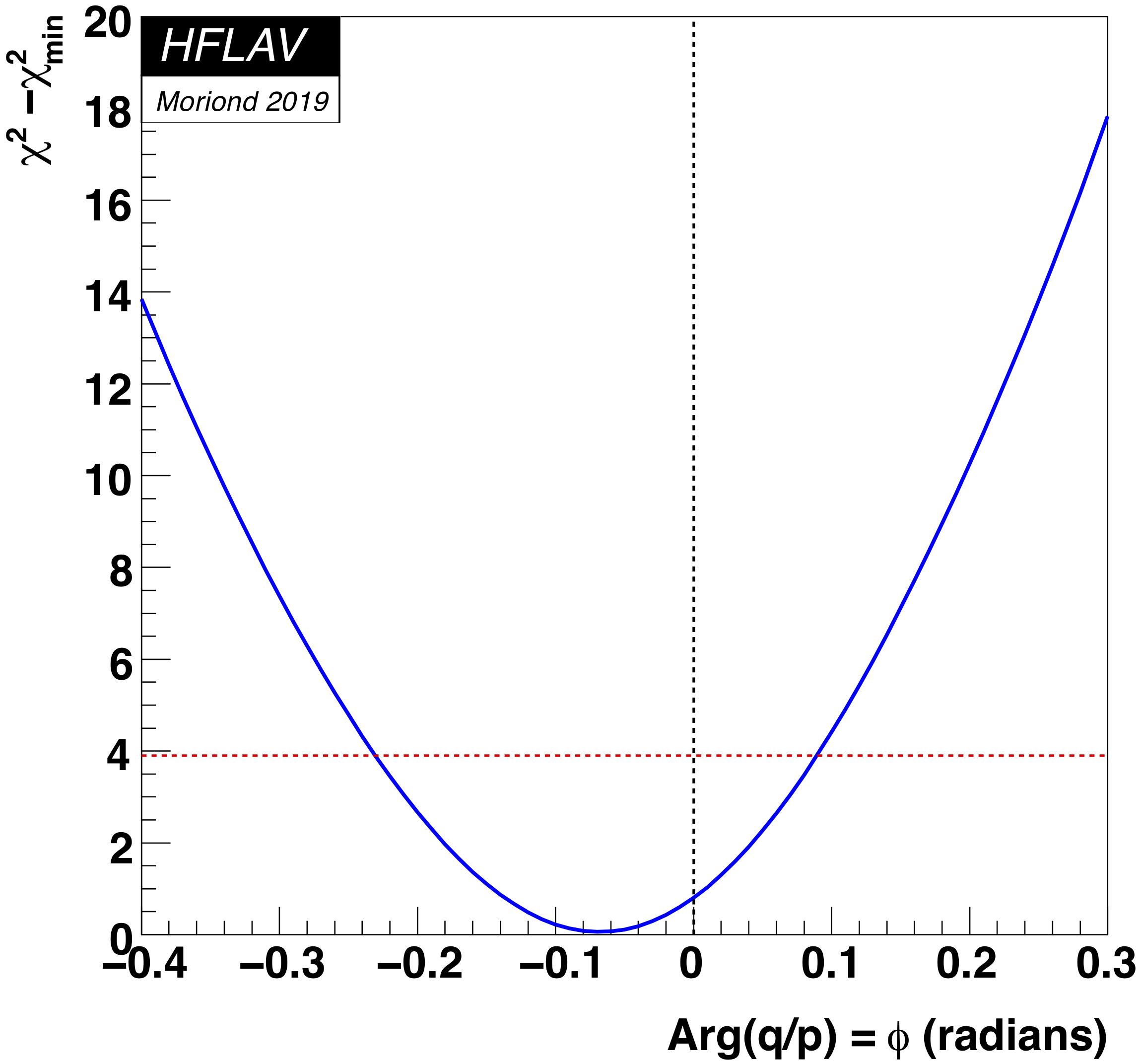
MNCONTOUR-like 1-d plots (click on for .eps versions):
red
dashed horizontal line denotes Δχ 2 = 3.84, corresponding to
95% C.L. interval. Cusp points result from multiple solutions.
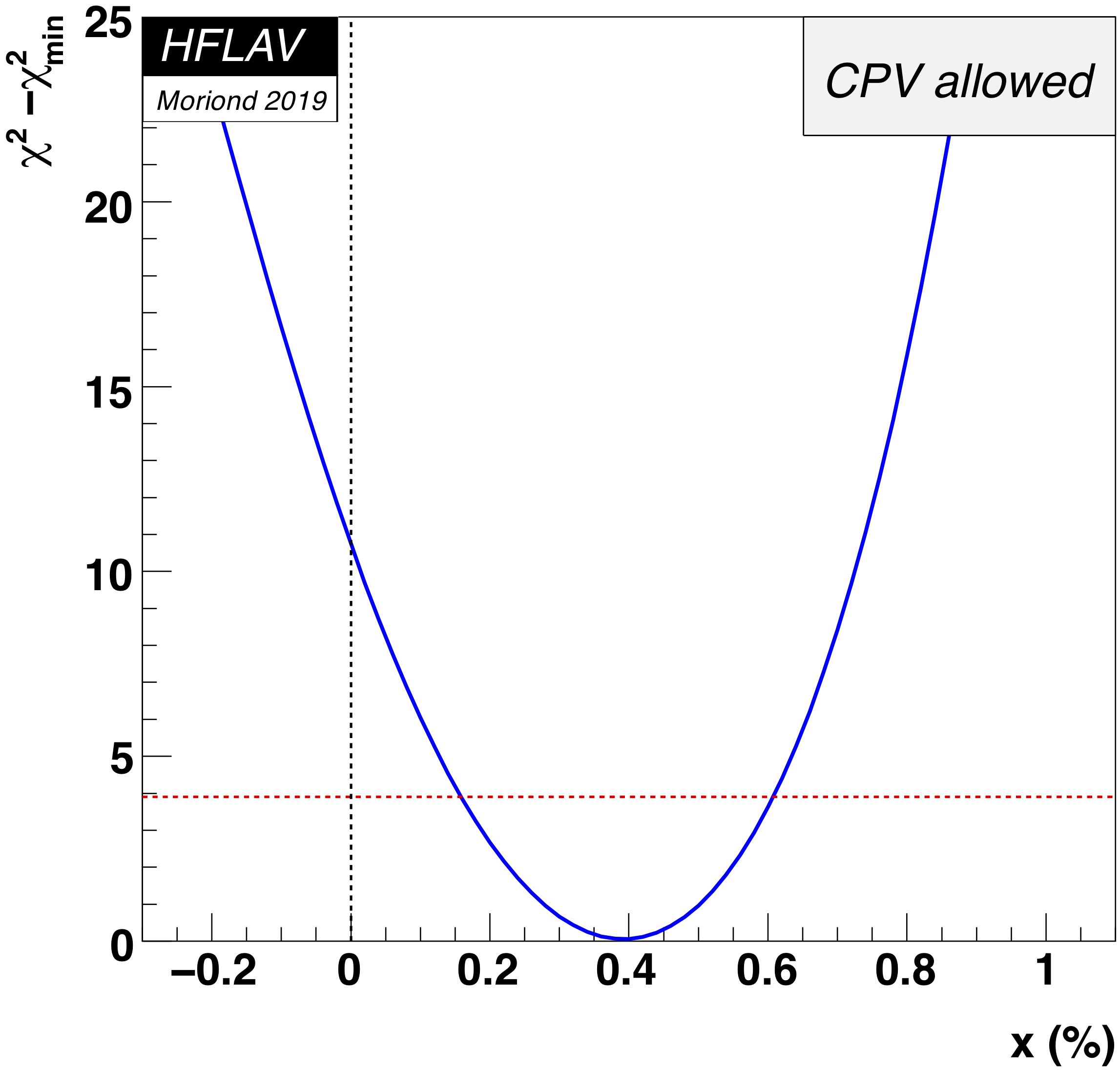
x = 0 point:
Δ χ 2 = 10.68,
x ≤ 0 excluded at 3.1σ
y = 0 point:
Δ χ 2 = 142.0,
y ≤ 0
excluded at > 11.4σ (limit of PROB routine)

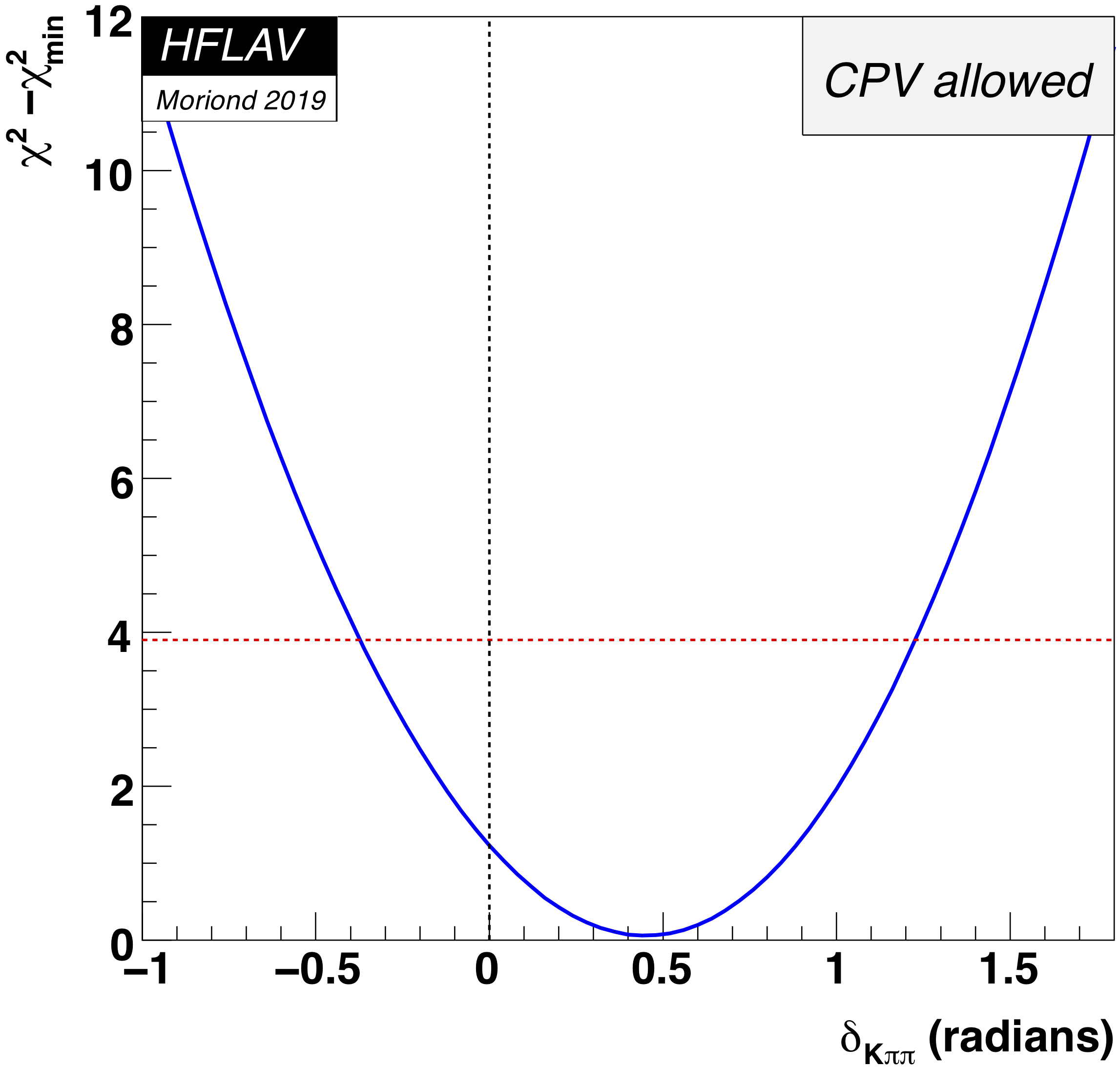
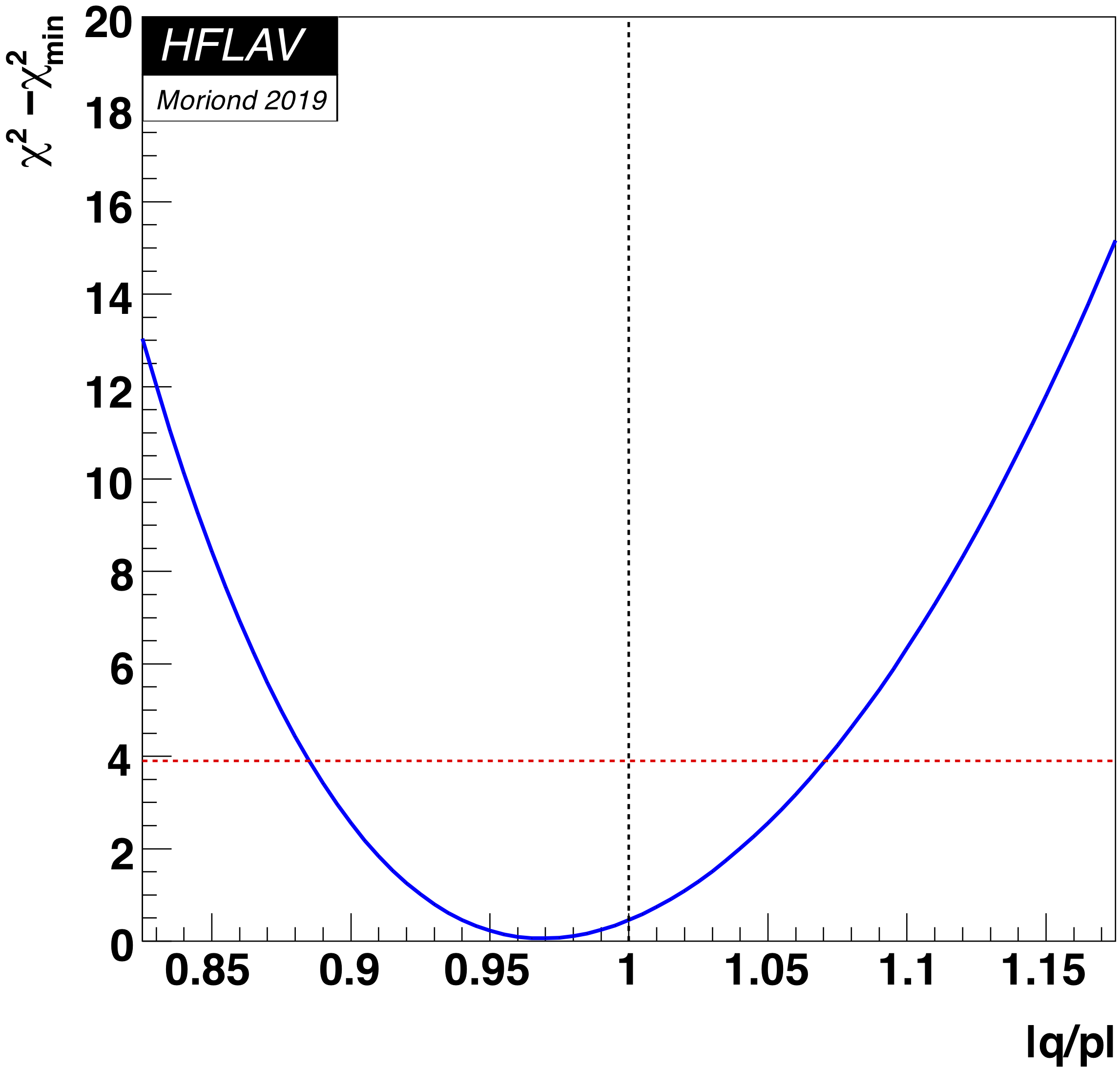
This page is maintained by
A. Schwartz
and was last updated












