Global Fit for D0-D0
Mixing and CP Violation
(through 14 September 2025)
People working on this:
Alan Schwartz,
Marco Gersabeck
For a complete list of references click
here
For world average values of measured observables (used below) click
here
Notation and Phase Convention:
The mass eigenstates are denoted
D 1 ≡ p|D0> +
q|D0> and
D 2 ≡ p|D0> −
q|D0>;
δ and δKππ are strong phase differences
between
D0
→ f and D0 → f amplitudes, and
φ is the weak phase difference Arg(q/p). We define
δ ≡
δ D0 → K−n(π)
−
δ D0
→ K−n(π).
The mixing parameters are defined as
x ≡ (m2 − m1)/Γ and
y ≡ (Γ2 − Γ1)/(2Γ), where
Γ = (Γ1 + Γ2)/2.
Our convention is (CP)|D0> =
−|D0>
and
(CP)|D0> =
−|D0>; thus, in the absence of CP violation,
x = (mCP+ − mCP−)/Γ and
y = (ΓCP+ − ΓCP−)/(2Γ).
Experimental Observables:
For this version of the global fit, there are input 63 experimental measurements:
y CP ,
A Γ ,
(x, y, |q/p|, φ) Belle
K0S π+ π − ,
(xCP, yCP, Δx, Δy) LHCb
K0S π+ π − (Runs 1, 2),
(x, y) BaBar
K0S h+ h− ,
(x, y) BaBar
π0 π+ π− ,
(R M )/2 LHCb
K+ π− π+ π − ,
(R M ) semileptonic ,
(x", y")
BaBar K+ π− π 0 ,
(R D , x2, y, cos δ, sin δ)
CLEOc Ψ(3770) ,
(ACPKπ) BESIII Ψ(3770) ,
(RD, AD, x'2±,
y'±)BaBar K+ π − ,
(RD, x'2, y')
Belle K+ π − ,
(RD, x'2, y') CDF K+ π − ,
(RD±, x'2±, y'±)
LHCb K+ π − (D*+B tagged),
(RKπ, cKπ, c′Kπ,
AKπ, ΔcKπ, Δc′Kπ,
ÃKπ, Δc̃Kπ, Δc̃′ Kπ)
LHCb K+ π − (D* tagged),
(ACPK, ACPπ) BaBar ,
(ACPK, ACPπ) Belle ,
(ACPK, ACPπ) CDF ,
(ACPK −ACPπ) LHCb (D*+B tagged) ,
(ACPK) LHCb (D* tagged)
Theoretical Parameters:
There are two equivalent sets of parameters governing mixing and indirect CP violation:
x, y, |q/p|, Arg(q/p) ≡ φ
and
x12, y12,
Arg(M12) ≡ φ2M,
Arg(Γ12) ≡ φ2Γ.
For both sets, the first two parameters govern mixing, and the latter two parameters govern indirect CP violation.
In addition to these four parameters, there are six additional parameters fitted:
δ, δKππ
are strong phases;
RD
is the ratio
Γ(D0→
f)/Γ(D0 → f); and
AD, Aπ, AK
are direct CP-violating parameters for
D0 → K+ π−,
D0 → π+ π−, and
D0 → K+ K−, respectively.
The subscript 2 for
φ2M and φ2Γ
denotes the basis in which the dominant U-spin-changing (ΔU=2) dispersive
and absorptive mixing amplitudes are real; see
Kagan and Silvestrini Eq. 107.
Choosing a basis ensures that the phases φ,
φ2M, and φ2Γ
are physically meaningful.
The relationships between
x, y, |q/p|, φ, δ, δKππ, RD,
AD, Aπ, AK
and the measured observables are given below. The observables appear in
blue
(left side), and the fitted parameters appear in
magenta
(right side).

The relationships between
(x, y, |q/p|, φ)
and
(x12, y12, φ2M, φ2Γ)
are:

The first three relations correspond to Eqs. (14), (15), and (48) of
Kagan and Sokoloff;
the last relation corresponds to Eq. (110) of
Kagan and Silvestrini.
Note that if φ2M = φ2Γ,
then |x| = x12, |y| = y12, |q/p| = 1, and
φ = −φ2M. In this case,
there is no CP violation in mixing.
Measurements used:
| Index |
Observable |
Value |
Source |
| 1 |
y CP − y CP (Kπ) |
(0.697 ± 0.028)% |
|
| 2 |
A Γ |
(0.0089 ± 0.0113)% |
World average (COMBOS combination)
of D0 → K+ K− /
π+ π − results
|
| |
|
| 0.40 ± 0.17 ± 0.04 |
| 0.29 ± 0.14 ± 0.03 |
| |
| (0.58 ± 0.19 +0.0734 −0.1177 )%
|
| (0.27 ± 0.16 +0.0546 −0.0854 )%
|
| 0.82 +0.20 −0.18
+0.0807 −0.0645
|
| (−13 +12 −13
+4.15 −4.77 ) degrees |
|
|
Belle + Belle II D0 → K0 S
π+ π − results using |
| 951 fb−1 and 408 fb−1, respectively.
The correlation is negligible. |
| |
|
Belle D0 → K0 S
π+ π − results using
921 fb−1. Correlation coefficients: |
| 1 | | 0.054 | |
−0.074 | | −0.031 |
| 0.054 | | 1 | |
0.034 | | −0.019 |
| −0.074 | | 0.034 |
|
1 | | 0.044 |
| −0.031 | | −0.019 | |
0.044 | | 1 |
|
| |
| x (no CPV) |
| y (no CPV) |
| |
| xCP |
| yCP |
| Δx |
| Δy |
| |
| xCP |
| yCP |
| Δx |
| Δy |
|
| (−0.86 ± 0.53 ± 0.17)% |
| (0.03 ± 0.46 ± 0.13)% |
| |
| (0.27 ± 0.16 ± 0.04)% |
| (0.74 ± 0.36 ± 0.11)% |
| (−0.053 ± 0.070 ± 0.022)% |
| (0.06 ± 0.16 ± 0.03)% |
| |
| (0.400 ± 0.045 ± 0.020)% |
| (0.551 ± 0.116 ± 0.059)% |
| (−0.029 ± 0.018 ± 0.001)% |
| (0.031 ± 0.035 ± 0.013)% |
|
|
LHCb
D0 →
K0S π+π −
results using 1 fb-1 (√s = 7 TeV) |
|
D*+ → D0π+ flavor tag.
Correlation coefficient = +0.37, no CPV. |
| |
|
3 fb-1 results (√s = 7, 8 TeV) allowing for CPV. |
|
D*+ → D0π+,
B → D0μ− X flavor tags.
Correlation coefficients (stat. + syst.): |
| 1 | | (−0.17 + 0.15) |
| (0.04 + 0.01) | |
(−0.02 − 0.02) |
| | | 1 |
| (−0.03 − 0.05) |
| (0.01 − 0.03) |
| | | | |
1 | | (−0.13 + 0.14) |
|
| |
|
5.4 fb-1 results (√s = 13 TeV) allowing for CPV. |
|
D*+ → D0π+,
B → D0μ− X flavor tags.
Correlation coefficients (stat. + syst.): |
| 1 | | (0.121 + 0.13) |
| (−0.018 + 0.01) | |
(−0.016 + 0.01) |
| | | 1 |
| (−0.012 − 0.02) |
| (−0.058 + 0.01) |
| | | | |
1 | | (0.069 + 0.31) |
|
| For (x, y, |q/p|, φ) → (xCP, yCP, Δx, Δy)
mapping, see
PRD 99, 012007 (2019)
|
|
| 15-16 |
|
| (0.16 ± 0.23 ± 0.12 ± 0.08)% |
| (0.57 ± 0.20 ± 0.13 ± 0.07)% |
|
|
BaBar
D0 →
K0S π+π − and
D0 →
K0S K+ K − combined; |
|
Correlation coefficient = +0.0615, no CPV. |
|
| 17-18 |
|
| (1.5 ± 1.2 ± 0.6)% |
| (0.2 ± 0.9 ± 0.5)% |
|
|
BaBar
D0 →
π0 π+π − |
|
Correlation coefficient = −0.006, no CPV. |
|
| 19 |
(x2 + y2)/2 |
(0.0130 ± 0.0269)% |
World average (COMBOS combination)
of
D0 → K+l− ν results |
| 20-21 |
|
| (2.61 +0.57 −0.68 ± 0.39)% |
| (−0.06 +0.55 −0.64 ± 0.34)% |
|
|
BaBar
K+ π − π 0 result;
correlation coefficient = −0.75. |
|
Note: x" = x cos δKππ + y sin δKππ,
y" = y cos δKππ − x sin δKππ. |
|
| 22-26 |
|
| (0.533 ± 0.107 ± 0.045)% |
| (0.06 ± 0.23 ± 0.11)% |
| (4.2 ± 2.0 ± 1.0)% |
| 0.81 +0.22−0.18
+0.07−0.05 |
| −0.01 ± 0.41 ± 0.04 |
|
CLEO-c Ψ(3770) results, 0.82 fb−1. Correlation coefficients:
| 1 | |
0 | |
0 | |
−0.42 | |
0.01 |
| | | 1 | |
−0.73 | | 0.39 | |
0.02 | |
| | | | |
1 | | −0.53 |
| −0.03 |
| | | | |
| | 1 |
| 0.04 |
| | | | |
| | |
| 1 |
|
| 27-29 |
|
| (0.303 ± 0.0189)% |
| (−0.024 ± 0.052)% |
| (0.98 ± 0.78)% |
|
BaBar
K+ π − results; correlation coefficients:
|
| 30-32 |
|
| (−2.1 ± 5.4)% |
| (−0.020 ± 0.050)% |
| (0.96 ± 0.75)% |
|
BaBar
K+ π − results; correlation coefficients
same as above.
|
|
|
|
| (0.353 ± 0.013)% |
| (0.009 ± 0.022)% |
| (0.46 ± 0.34)% |
|
Belle
K+ π − no-CPV results using 976 fb−1.
Correlation coefficients:
| 1 | | +0.737 | | −0.865 |
| | | 1 | | −0.948 |
| | | | | 1 |
|
| 36-38 |
|
| (0.351 ± 0.035)% |
| (0.008 ± 0.018)% |
| (0.43 ± 0.43)% |
|
CDF
K+ π − results for 9.6 fb−1.
Correlation coefficients:
|
| 39-47 |
| RKπ |
| c Kπ |
| c′Kπ |
| ÃKπ |
| Δc̃ Kπ |
| Δc̃′Kπ |
| AKπ |
| Δc Kπ |
| Δc′Kπ |
|
| (0.3427 ± 0.0019)% |
| (0.528 ± 0.033)% |
| (12.0 ± 3.5) × 10 −6 |
| (−0.82 ± 0.59)% |
| (0.032 ± 0.036)% |
| (−2.0 ± 3.8) × 10 −6 |
| (−0.9 ± 2.0)% |
| (−0.01 ± 0.10)% |
| (4.6 ± 9.8) × 10 −6 |
|
LHCb K+ π − results for
3.0 + 5.4 = 8.4 fb−1 (√s = 7, 8, 13 TeV)
D*+ → D0π+
flavor tag. Correlation coefficients:
| 1 | |
−0.927 | |
0.803 | |
0.008 | |
−0.007 | |
0.000 | |
0.003 | |
−0.002 | |
0.002 | |
| | |
1 | |
−0.943 | |
−0.014 | |
0.013 | |
−0.006 | |
−0.005 | |
0.004 | |
−0.004 | |
| | |
| |
1 | |
0.007 | |
−0.006 | |
0.000 | |
0.003 | |
−0.003 | |
0.003 | |
| | |
| |
| |
1 | |
−0.934 | |
0.810 | |
0.000 | |
0.000 | |
0.000 | |
| | |
| |
| |
| |
1 | |
−0.943 | |
0.000 | |
0.000 | |
0.000 | |
| | |
| |
| |
| |
| |
1 | |
0.000 | |
0.000 | |
0.000 | |
| | |
| |
| |
| |
| |
| |
1 | |
−0.938 | |
0.811 | |
| | |
| |
| |
| |
| |
| |
| |
1 | |
−0.943 | |
Note: above values in red (<1.5%) are neglected in the fit.
Definitions:
| dN±⁄dt
= RKπ± +
√(RKπ±)
(cKπ ± ΔcKπ) t +
(c′Kπ ± Δc′Kπ) t2 |
| where RKπ± ≡
RKπ (1 ± AKπ). Also: |
| ÃKπ = AKπ − 2adKK |
|
Δc̃Kπ = ΔcKπ −
cKπ adKK +
2AΓ √(RKπ) |
|
Δc̃′Kπ = Δc′Kπ −
2c′Kπ adKK +
2cKπ AΓ √(RKπ)
|
|
| 48-50 |
|
| (0.3500 ± 0.0073)% |
| (0.008 ± 0.015)% |
| (0.41 ± 0.20)% |
|
LHCb K+ π − results for
3.0 + 5.4 = 8.4 fb−1 (√s = 7, 8, 13 TeV)
B → D*+μ− X, D*+ → D0π+
flavor tags. Correlation coefficients:
| 1 | | 0.624 | | −0.749 |
| | | 1 | | −0.943 |
| | | | | 1 |
|
| 51-53 |
|
| (0.3440 ± 0.0074)% |
| (−0.005 ± 0.017)% |
| (0.68 ± 0.21)% |
|
LHCb K+ π − results for
3.0 + 5.4 = 8.4 fb−1 (√s = 7, 8, 13 TeV)
B → D*+μ− X, D*+ → D0π+
flavor tags. Correlation coefficients:
| 1 | | 0.629 | | −0.745 |
| | | 1 | | −0.946 |
| | | | | 1 |
|
| 54-55 |
|
| (0.00 ± 0.34 ± 0.13)% |
| (−0.24 ± 0.52 ± 0.22)% |
|
BaBar 385.8 fb−1 near ϒ(4S) resonance
|
| 56-57 |
|
| (−0.43 ± 0.30 ± 0.11)% |
| (0.43 ± 0.52 ± 0.12)% |
|
Belle 540 fb−1 near ϒ(4S) resonance
|
| 58-59 |
|
| (−0.32 ± 0.21)% |
| (0.31 ± 0.22)% |
|
|
CDF 9.7 fb−1
pp collisions at
√s = 1.96 TeV |
|
( 〈t〉K − 〈t〉π )
/ τD = 0.27 ± 0.01 |
|
| 60 |
ACPK − ACPπ |
(−0.154 ± 0.029)% |
|
LHCb 8.9 fb−1 pp collisions at
√s = 7, 8, 13 TeV |
| D*+ → D0π+
and
B → D0μ− X flavor tags |
|
( 〈t〉K − 〈t〉π )/τD
= 0.115 ± 0.002;
〈t〉/τD
= 1.71 ± 0.10
|
|
| 61 |
ACPK |
(0.068 ± 0.054 ± 0.016)%
|
|
LHCb 5.7 fb−1 pp collisions at
√s = 13 TeV |
| D*+ → D0π+ flavor tags |
|
〈t〉K /τD = (701.5 ± 1.1)/(410.3 ± 1.0) = 1.7097 ± 0.0050
|
|
| 62 |
(x2 + y2)/4 |
(0.0048 ± 0.0018)% |
|
LHCb
3.0 fb−1 pp collisions at
√s = 7, 8 TeV |
|
D0 →
K+ π − π + π −
|
|
| 63 |
ACPKπ |
0.132 ± 0.011 ± 0.007 |
|
BESIII Ψ(3770) results, 2.93 fb−1.
D0 → K− π+,
|
| difference between CP-even tagged and CP-odd tagged |
|
MINUIT fit results
Three main fits are performed, as follows:
Fit #1:
no indirect CP violation
This fit takes |q/p| = 1 and φ = 0. In addition, we neglect sub-leading amplitudes in
Cabibbo-favored (CF) and doubly Cabibbo-suppressed (DCS) decays, i.e., they proceed via tree
diagrams. This implies no direct CP violation in these decays, and AD = 0.
Fit #2:
One-parameter description of indirect CP violation
This parametrization results from two assumptions:
(1) sub-leading amplitudes in CF and DCS decays are negligible (AD = 0);
(2) sub-leading amplitudes in singly Cabibbo-suppressed (SCS) decays (i.e., loop amplitudes)
are neglected in indirect CP violation observables, as their contribution is suppressed
by the small mixing parameters x and y. As a consequence, only short-distance dispersive amplitudes
contribute to indirect CP violation.
Thus Arg(Γ12) = 0 (in the ΔU=2 basis, see note on Arg(q/p) above),
and all indirect CP violation is due to
Arg(M12) ≠ 0, or more formally
Arg(M12) ≠ Arg(Γ12).
This difference is denoted
φ12 ≡ Arg(M12/Γ12).
This reduces four mixing + CP violation parameters to three: x12, y12, φ12.
For alternative parameters (x, y, |q/p|, φ), this introduces a constraint among them, first derived by
Ciuchini et al.
and later independently by
Kagan and Sokoloff:
tanφ =
(1-|q/p|2)⁄(1+|q/p|2)
×
(x⁄y).
Alternatively, one can use the quadratic equation (15) of
Grossman, Nir, and Perez
to reduce four parameters to three.
We perform this fit three times:
once for parameters x, y, φ (giving MINOS errors for φ);
once for parameters x, y, |q/p| (giving MINOS errors for |q/p|); and
once for parameters x12, y12, φ12.
Fit #3:
Two-parameter description of indirect CP violation
In this parameterization,
sub-leading amplitudes in SCS decays are accounted for in indirect CP violation observables.
Such sub-leading amplitudes contribute to Γ12 in addition to M12,
and thus Arg(Γ12) can be nonzero. We thus fit for all four parameters:
(x12, y12, φ2M, φ2Γ)
or equivalently (x, y, |q/p|, φ). We perform this fit twice:
(a) neglecting sub-leading amplitudes in CF and DCS decays, i.e., AD = 0; and
(b) allowing all sub-leading amplitudes, i.e., floating all ten parameters. The results
are essentially identical except for a slight shift in the φ central value:
(−1.46 ± 1.04)° → (−1.51 ± 1.04)°.
The MINUIT output for Fits #1 − #3 are given here.
In this output, x, y, R D, A D, A π and A K are in
percent; and δ, δ2 (= δKππ), and φ are in radians.
Correlation coefficients among parameters are listed at the end. The final results are:

χ 2 contributions for the all-CPV-allowed fit #3:
 _____________________________________________
_____________________________________________
MNCONTOUR-like 2-d plots:
(click on for .eps versions)

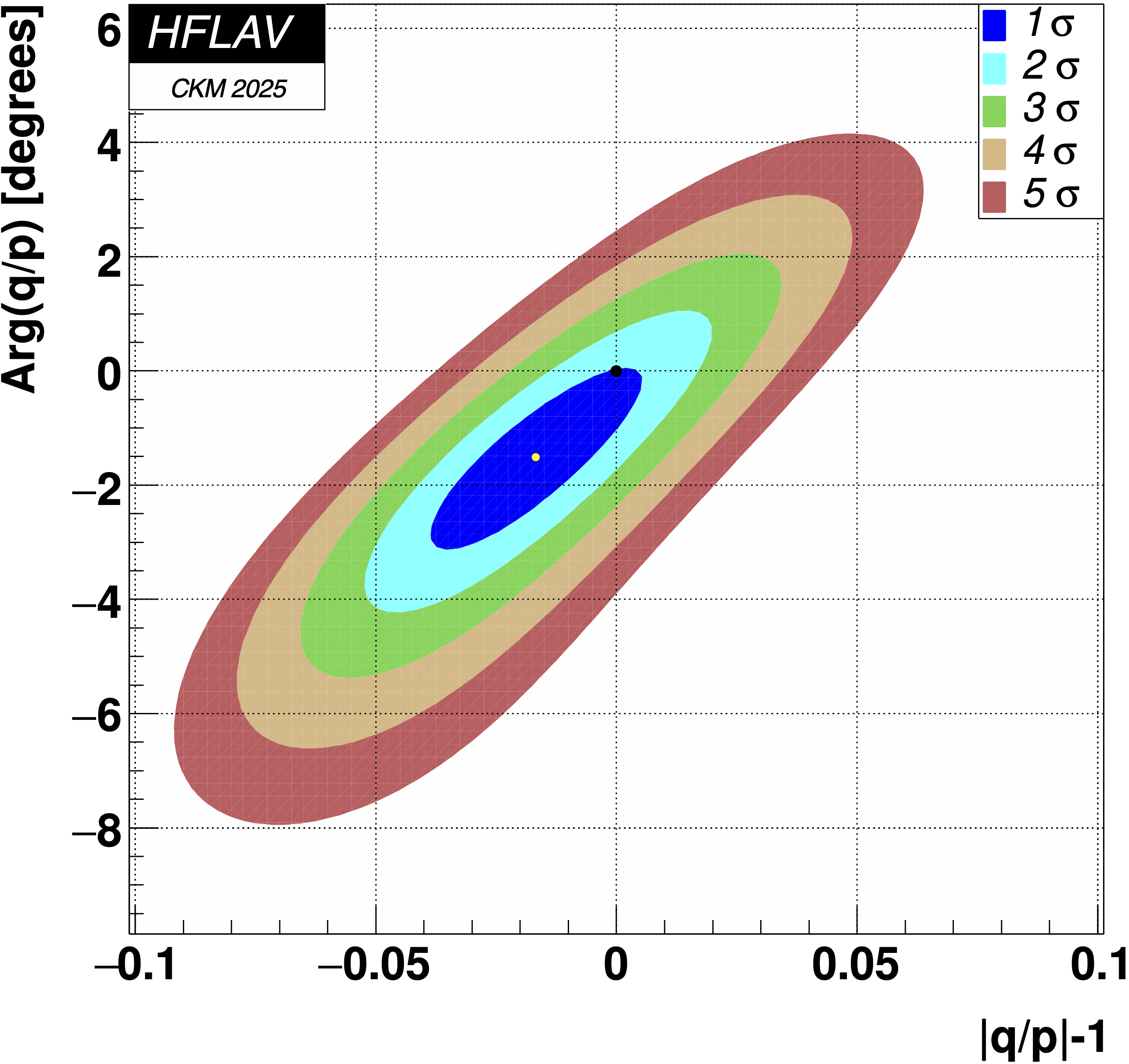
CPV-allowed plot, no mixing (x,y) = (0,0) point:
Δχ2 = 4328,
excluded at ≫ 11.5σ (limit of CERNLIB PROB routine)
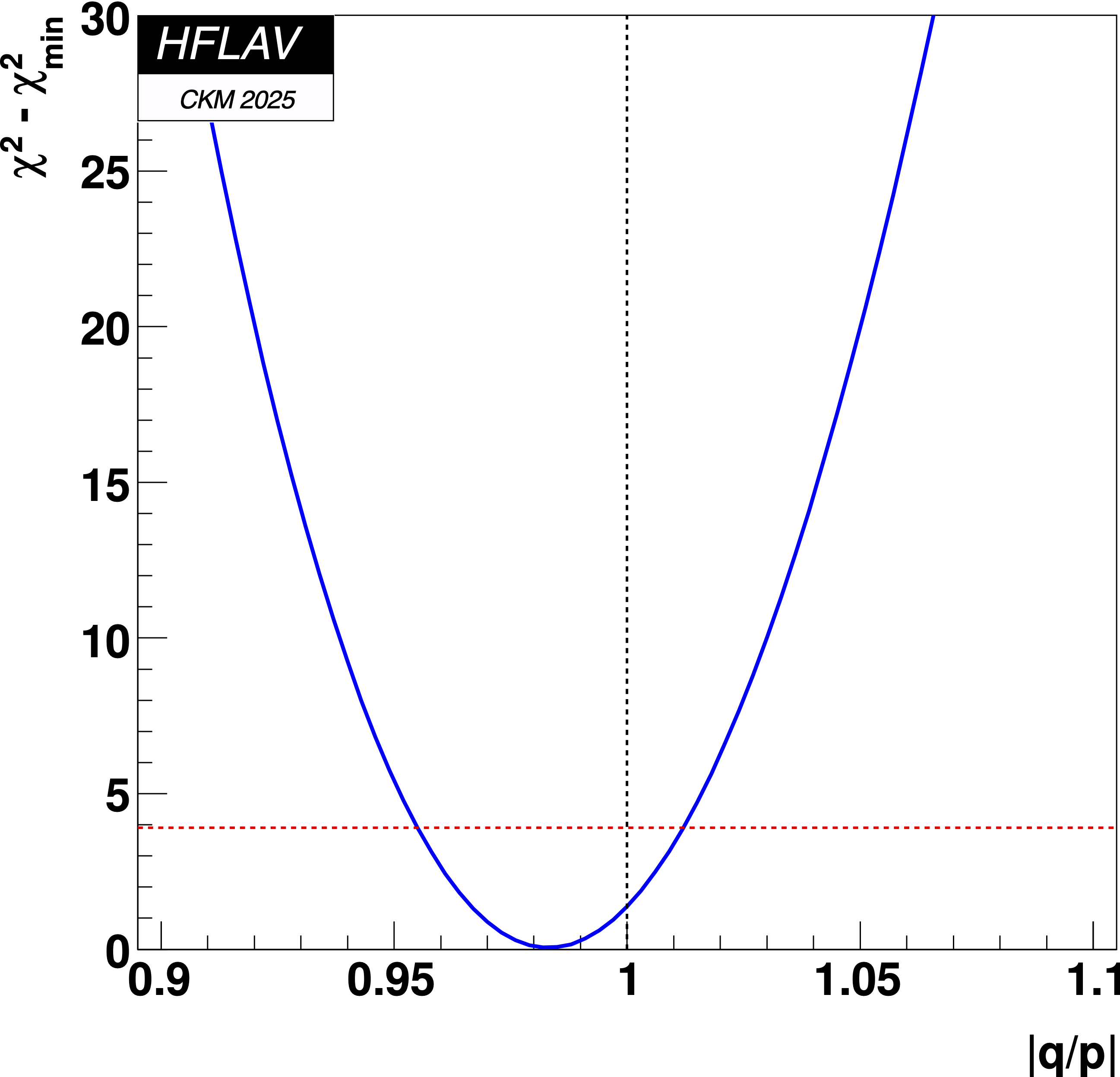
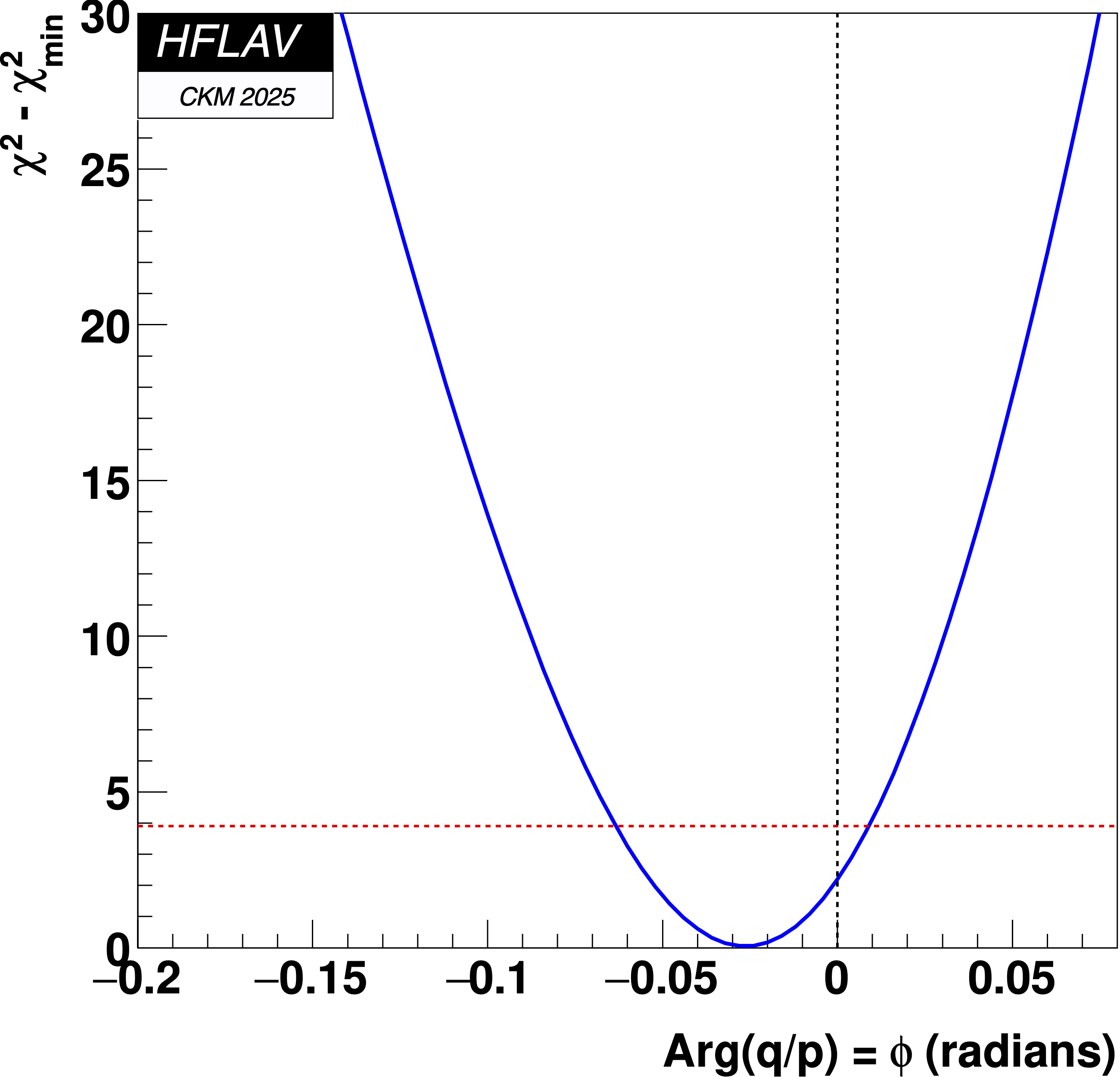
No indirect CP violation point (|q/p|, φ) = (1,0):
Δχ2 = 2.16, consistent with CP conservation (0.95σ)


No indirect CP violation point (φ2M, φ2Γ) = (0,0):
Δχ2 = 1.97, consistent with CP conservation (0.89σ)
Note:
the slight difference from the (|q/p|, φ) plot is due to the constraint AD = 0.
(This raises the χ2 of the best-fit point, slightly lowering Δχ2
of the no-CPV point.)
_____________________________________________
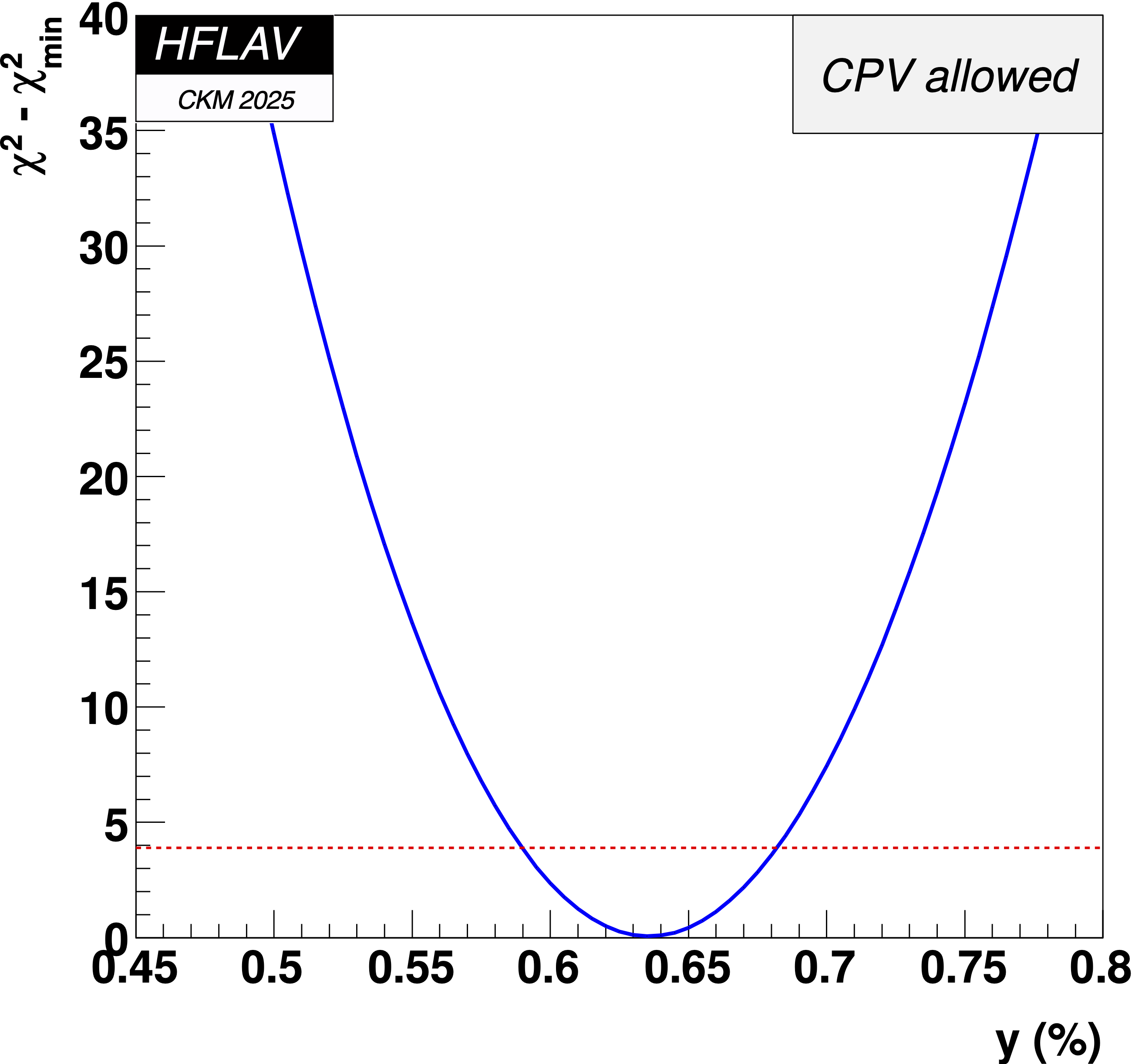
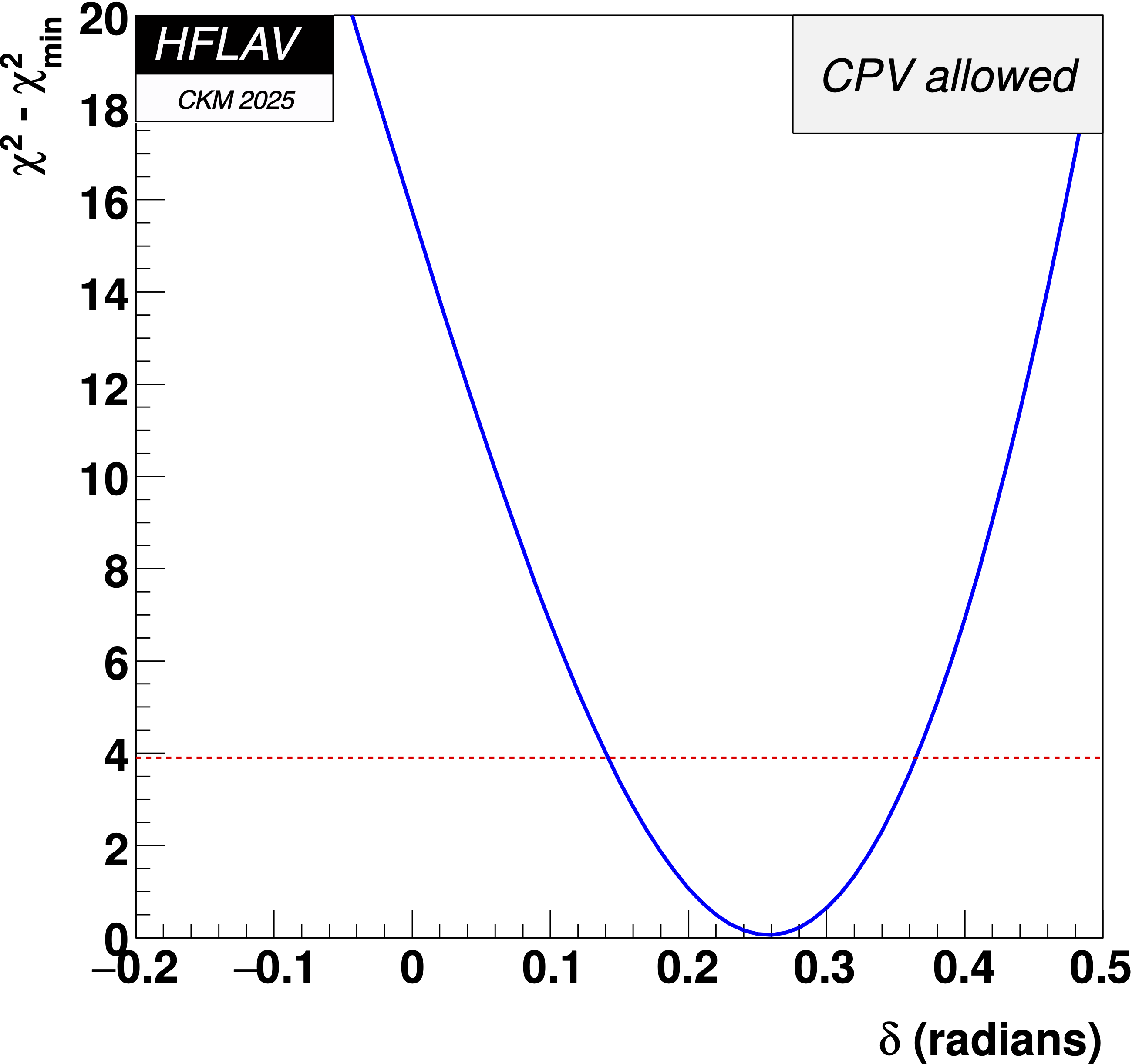
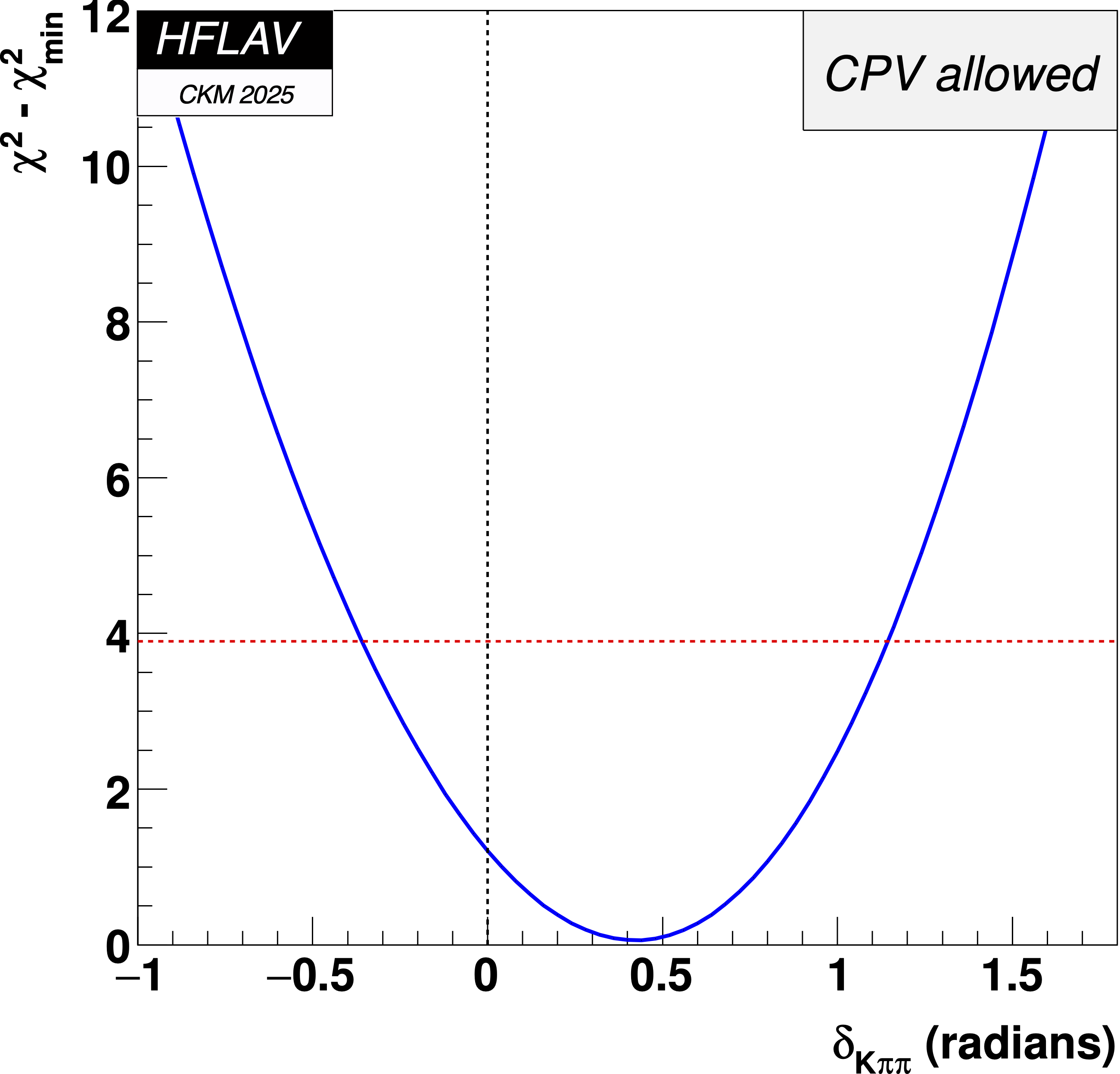
MNCONTOUR-like 1-d plots:
Dashed red
horizontal line denotes Δχ2 = 3.84, corresponding to
a 95% C.L. interval.
(click on for .pdf versions)

x = 0 point:
Δχ2 = 87.0,
x ≤ 0 excluded at 9.3σ
y = 0 point:
Δχ2 = 1220,
y ≤ 0
excluded at > 11.5σ (limit of CERNLIB PROB)
This page is maintained by
A. Schwartz
and was last updated








